Postulado de Eudoxo-Arquímedes
Dadas dos magnitudes homogéneas, no congruentes ni nulas, existe un número natural n tal que, al multiplicar la magnitud menor por n, esta sobrepasa a la mayor.
Si tomamos dos magnitudes homogéneas (misma unidad de medida), no congruentes (con distinto valor) y distintas de cero, siempre existirá un múltiplo de la magnitud menor que supere a la mayor.
En otras palabras, este postulado afirma que es posible añadir un número suficiente de copias de la magnitud menor para sobrepasar la mayor.
Nota. Este principio fue formulado de manera independiente por los matemáticos griegos Eudoxo de Cnido y Arquímedes de Siracusa. También se conoce como “principio de Arquímedes” o “principio de Eudoxo”.
Un ejemplo práctico
Consideremos dos segmentos AB y CD.
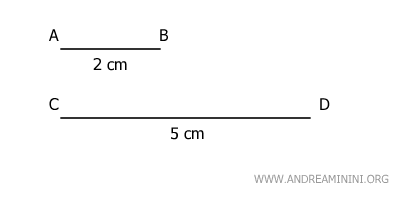
El segmento AB mide 2 cm, mientras que el segmento CD mide 5 cm.
Es evidente que la magnitud menor es el segmento AB.
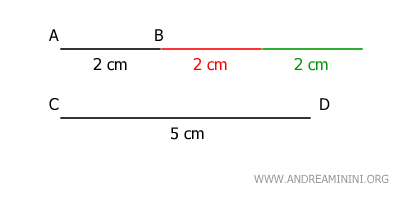
En este caso, el múltiplo de AB con n=3 supera la longitud de CD.
$$ 3 \cdot \overline{AB} > \overline{CD} $$
$$ 3 \cdot 2 \ cm > 5 \ cm $$
$$ 6 \ cm > 5 \ cm $$
En otras palabras, basta con añadir dos segmentos más, iguales a AB, para sobrepasar la longitud de CD.

Observaciones
Algunas consideraciones y notas relacionadas con el postulado:
- Con frecuencia, el principio de Eudoxo-Arquímedes se interpreta como un antecedente del concepto de límite, fundamental para el desarrollo del cálculo diferencial e integral.
- Este principio también guarda relación con la teoría de la medida y la integración, pues constituye la base conceptual de las sumas de Riemann, esenciales para definir la integral de Riemann.
Nota. Resulta fascinante comprobar cómo ideas matemáticas concebidas hace miles de años siguen siendo pilares fundamentales de la teoría matemática contemporánea.
Y así sucesivamente.