El espacio en geometría

El espacio es un concepto esencial en geometría. Está constituido por infinitos planos y, en términos generales, funciona como el “contenedor” en el que se sitúan las figuras sólidas.

En la geometría euclidiana, el término “espacio” suele referirse al espacio tridimensional (x, y, z). Es importante destacar esta precisión, ya que en matemáticas el concepto de espacio puede extenderse a dimensiones superiores.

Cada figura geométrica sólida (como cubos, prismas rectangulares, esferas, etc.) puede considerarse como un conjunto de puntos distribuidos sobre distintos planos.

La rama de la geometría que estudia las propiedades de estas figuras en el espacio se denomina geometría del espacio.

Nota: Las figuras geométricas sólidas son cuerpos tridimensionales que permiten analizar tanto sus formas como sus propiedades geométricas y físicas. A diferencia de las figuras planas, limitadas al estudio de la forma y el perímetro, las figuras tridimensionales ofrecen profundidad y volumen, ampliando significativamente las posibilidades de análisis.

En geometría euclidiana, el espacio se representa habitualmente mediante coordenadas cartesianas (x, y, z), que permiten precisar la posición de los puntos en las tres dimensiones: longitud, anchura y altura.

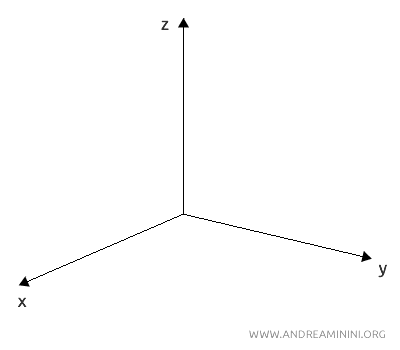
Por ejemplo, un cubo es un sólido limitado por seis caras cuadradas, cuyos vértices pueden definirse mediante coordenadas en el espacio.

Los puntos de un cubo se sitúan sobre diferentes planos que se intersectan perpendicularmente.

 

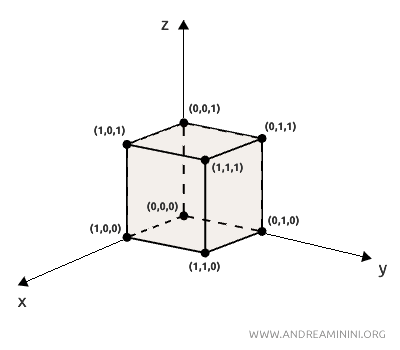
Para representar un cubo en un sistema cartesiano, se pueden asignar coordenadas a sus vértices, como (0, 0, 0), (0, 1, 0), (1, 1, 0), entre otras.

Rectas en el espacio

Las rectas en el espacio pueden encontrarse en un mismo plano o estar ubicadas en planos distintos.

Cuando dos rectas se hallan en el mismo plano, se denominan rectas coplanares. Según su disposición, pueden cortarse en un único punto o ser paralelas, sin llegar a intersectarse jamás.

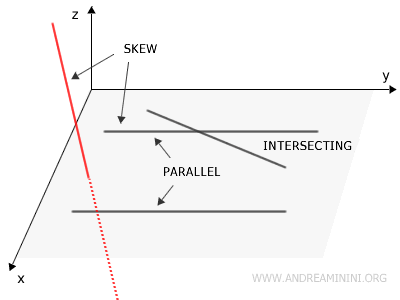
Las rectas situadas en planos diferentes se llaman rectas alabeadas y nunca se cruzan.

¿Por qué no se cruzan las rectas alabeadas? Las rectas alabeadas, por definición, no están contenidas en un mismo plano, lo que impide que puedan intersectarse. Para demostrarlo, supongamos - en contra de la definición - que dos rectas alabeadas, r₁ y r₂, tienen un punto común P.

En ese caso, podría elegirse un punto A sobre una de las rectas y un punto B sobre la otra, ambos distintos de P. Los tres puntos, P, A y B, definirían un plano β que contendría a ambas rectas, lo cual significaría que son coplanares. Sin embargo, la esencia de las rectas alabeadas es precisamente no ser coplanares. Por tanto, si dos rectas se intersectan, deben estar contenidas en el mismo plano y no pueden ser alabeadas.

Planos en el espacio

El espacio está constituido por infinitos planos, que solo pueden relacionarse entre sí de dos maneras:

• Planos paralelos
  Son aquellos que nunca se cortan y permanecen a la misma distancia en todos sus puntos. Un ejemplo cotidiano serían los pisos de distintos niveles en un edificio: mientras no haya deformaciones estructurales, se encuentran en planos paralelos.
  
• Planos secantes
  Cuando dos planos no son paralelos, se intersectan, y su intersección es siempre una recta.
  

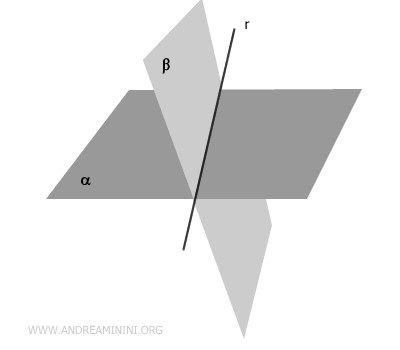
En el espacio tridimensional, dos planos no pueden intersectarse en un único punto; su intersección, si existe, es necesariamente una recta (demostración).

La relación de paralelismo entre planos cumple las siguientes propiedades:

• Reflexiva
  Un plano siempre es paralelo a sí mismo.
• Simbólica
  Si el plano A es paralelo al plano B, entonces el plano B es paralelo al plano A.
• Transitiva
  Si el plano A es paralelo al plano B y el plano B es paralelo al plano C, entonces el plano A es paralelo al plano C.

La posición de una recta respecto a un plano en el espacio tridimensional puede clasificarse de la siguiente manera:

• Recta coplanar
  La recta se encuentra completamente contenida en el plano, es decir, todos sus puntos pertenecen a dicho plano.
  
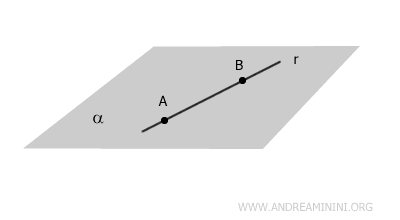
• Recta secante
  La recta intersecta al plano en un único punto.
  
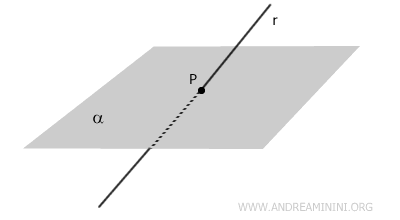
• Recta paralela
  La recta no tiene ningún punto en común con el plano.
  

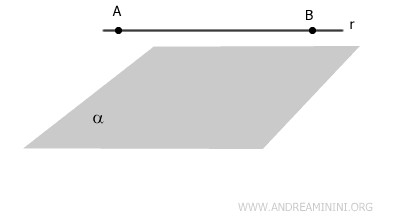
Estas relaciones son fundamentales para comprender la geometría tridimensional.

Postulados del espacio

Entre los postulados fundamentales del espacio en geometría se encuentran:

• Por tres puntos distintos y no colineales pasa un único plano.
  
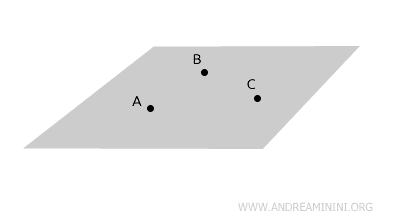
• Por cualesquiera dos puntos distintos de un plano, la recta que los une se encuentra contenida por completo en dicho plano.
  
• Postulado de separación
  Un plano divide los puntos del espacio que no se encuentran en él en dos regiones denominadas semiespacios. El propio plano constituye el límite común de ambos semiespacios.
  
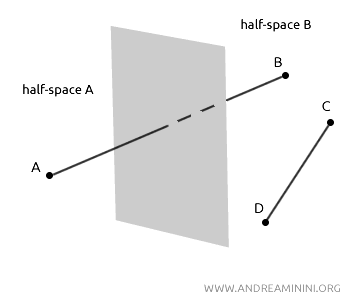
  Si dos puntos, A y B, se encuentran en semiespacios opuestos, el segmento AB intersectará el plano. Por el contrario, si dos puntos, C y D, se encuentran en el mismo semiespacio, el segmento CD no lo cortará.

Notas adicionales

Algunos apuntes adicionales sobre el espacio en geometría:

• El espacio en física
  En física, el espacio es un concepto clave en la teoría de la relatividad. Albert Einstein lo redefinió, dejándolo de concebir como algo fijo para integrarlo en una entidad única junto con el tiempo, conocida como espacio-tiempo. Este concepto explica fenómenos como la dilatación temporal o la contracción espacial bajo velocidades extremas o campos gravitatorios intensos. No obstante, estas ideas no se aplican al espacio geométrico clásico.

Y así sucesivamente.