Extensión de los sólidos
En geometría tridimensional, la extensión de un sólido se refiere al espacio que ocupa un cuerpo en tres dimensiones.
A diferencia de la longitud o el área, la extensión no se mide directamente. Es un concepto primitivo, es decir, una noción básica que se acepta sin necesidad de definición formal. La comprendemos de manera intuitiva a través de la experiencia cotidiana.
Por ejemplo, al observar un objeto tridimensional - una caja, una esfera o una pirámide - lo primero que percibimos es el espacio que ocupa: cuán "grande" o "pequeño" nos parece.
Ese espacio no es solo una magnitud física: es una idea fundamental sobre la que se construyen los conceptos de volumen, equivalencia y congruencia entre sólidos.
De forma natural, reconocemos que dos cuerpos tienen la misma extensión cuando ocupan el mismo volumen, aunque sus formas sean distintas.
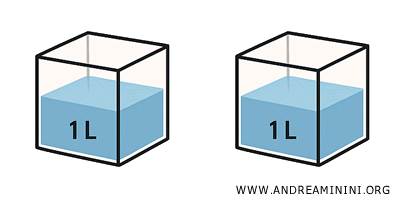
Ejemplo. Si vertemos un litro de agua en una botella, un cubo o una esfera, todos los recipientes se llenan por completo. Aunque las formas varíen, el espacio ocupado - su extensión - es idéntico.
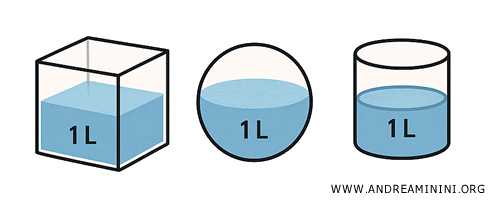
En geometría, utilizamos el concepto de volumen para cuantificar y comparar extensiones. El volumen depende únicamente del espacio ocupado, no de la forma del cuerpo.
Equivalencia entre sólidos
Decimos que dos sólidos, A y B, son equivalentes cuando tienen la misma extensión. $$ A \doteq B $$ El símbolo $ \doteq $ indica equivalencia.
Esta relación es similar a las relaciones de equivalencia que se estudian en aritmética o teoría de conjuntos, y cumple con tres propiedades fundamentales:
- Reflexividad: Todo sólido es equivalente a sí mismo.
- Simetría: Si A es equivalente a B, entonces B también lo es a A.
- Transitividad: Si A es equivalente a B y B a C, entonces A es equivalente a C.
Estas propiedades definen lo que en matemáticas se conoce como una relación de equivalencia.
Así, podemos clasificar los sólidos en clases de extensión: conjuntos de cuerpos que ocupan el mismo volumen, aunque puedan tener formas diferentes.
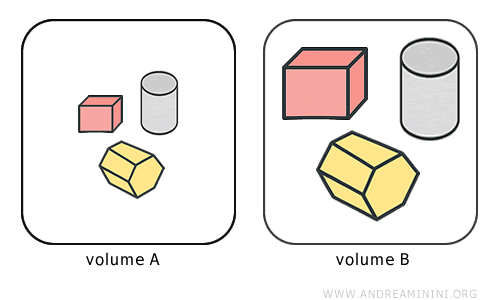
El volumen actúa como medida numérica de la extensión. Por tanto, cada clase de extensión está asociada a un valor de volumen determinado.
¿Cómo saber si dos sólidos son equivalentes?
Un método habitual consiste en dividir un sólido en unidades más pequeñas de volumen, para luego reorganizarlas formando nuevas figuras.
Por ejemplo, si se fragmenta un sólido en cuatro cubos iguales, estos pueden disponerse de distintas formas para construir otros cuerpos.
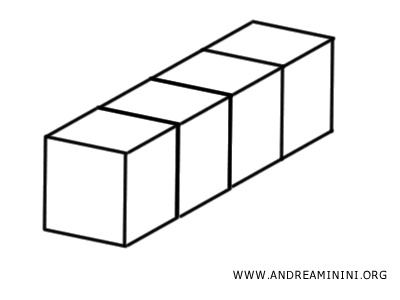
El cuerpo resultante tendrá la misma extensión que el original, ya que el volumen total permanece constante: no se ha añadido ni eliminado materia, solo redistribuida. Por tanto, los dos sólidos son equivalentes y poseen el mismo volumen.
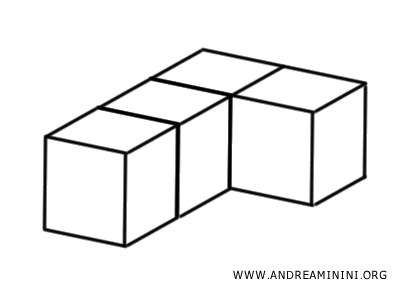
No obstante, la forma del nuevo cuerpo puede ser distinta, lo que significa que no son congruentes.
Es como jugar con bloques de construcción: mientras uses las mismas piezas, el volumen no cambia, aunque la forma final sí lo haga.
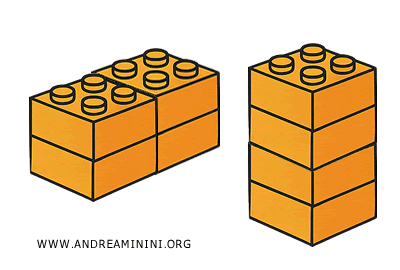
Diferencia entre congruencia y equivalencia
La congruencia y la equivalencia no son lo mismo:
- Sólidos congruentes: Tienen exactamente la misma forma y tamaño. Por lo tanto, siempre son equivalentes.
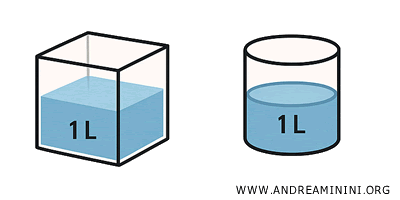
- Sólidos equivalentes: Comparten el mismo volumen, aunque pueden tener formas diferentes. Por ejemplo, un cilindro y un prisma pueden tener la misma altura y volumen, pero estructuras distintas. Son equivalentes, pero no congruentes.
Comprender la idea de extensión es clave para entender el volumen y realizar comparaciones significativas entre cuerpos tridimensionales.
Gracias a este concepto, podemos afirmar que una botella de un litro contiene siempre el mismo volumen, sin importar su forma exterior.
En definitiva, la extensión no se percibe directamente: se revela mediante la medición del volumen. Así como dos libros con formas distintas pueden ocupar el mismo hueco en una estantería, dos sólidos con geometrías diferentes pueden tener el mismo volumen.
Y así sucesivamente.