Tronco de Pirámide

Un tronco de pirámide es un sólido geométrico que se obtiene al seccionar una pirámide mediante un plano paralelo a su base. Esta sección genera una nueva cara, de menor tamaño que la base original, y transforma la pirámide en un sólido con dos bases paralelas.

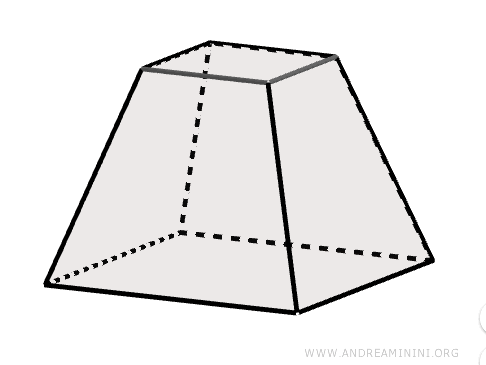
Cuando una pirámide se corta con un plano paralelo a su base, queda dividida en dos sólidos distintos:

• Una pirámide menor situada en la parte superior, con vértice \( V \) y base \( A'B'C'D' \). Esta nueva pirámide comparte el mismo vértice que la pirámide original \( ABCDV \), y ambas son semejantes entre sí.
• Un tronco de pirámide, que queda en la parte inferior, limitado por dos bases poligonales paralelas y caras laterales que tienen forma de trapecio.

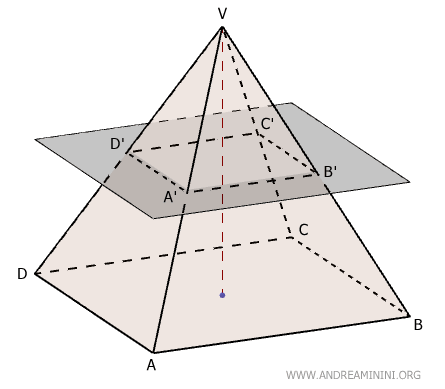
En un tronco de pirámide, las bases son paralelas y semejantes, aunque de distinto tamaño.

La base mayor (ABCD) coincide con la base original de la pirámide, mientras que la base menor (A'B'C'D') corresponde a la sección generada por el plano de corte.

Las caras laterales del tronco tienen forma trapezoidal. En el caso particular de una pirámide regular, dichas caras laterales son trapecios isósceles.

El número de caras laterales coincide con el número de lados de la base de la pirámide.

Esta regla se cumple tanto si la base es un polígono regular como si es irregular.

Los siguientes conceptos, que se aplican también a otros sólidos poliédricos, son fundamentales en el estudio del tronco de pirámide:

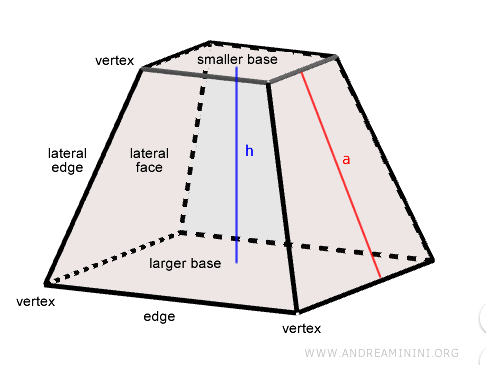
• La altura (h) es la distancia perpendicular entre las dos bases.
• Los vértices del tronco son los vértices de ambas bases, la mayor y la menor.
• Las aristas laterales son los segmentos que unen los vértices correspondientes de las dos bases.
• La apotema (a) se utiliza para calcular el área lateral.

Un tronco de pirámide regular es aquel que se obtiene a partir de una pirámide regular. Se caracteriza porque sus caras laterales son trapecios isósceles congruentes, y la altura de cada trapecio coincide con la apotema del tronco. Se denomina tronco recto si procede de una pirámide recta, es decir, una pirámide cuyo vértice se encuentra alineado con el centro de la base y cuyo eje es perpendicular al plano de la base.

Fórmulas

Las fórmulas para calcular el área y el volumen de un tronco de pirámide son las siguientes:

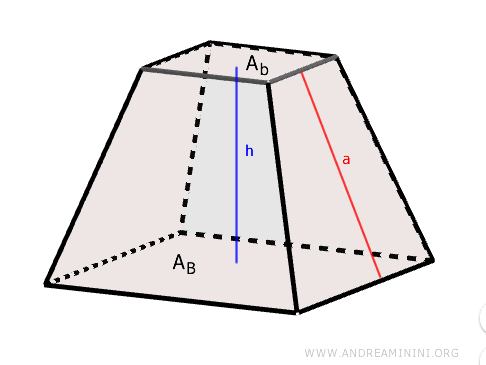
• Área Lateral (A_l)
  Se obtiene sumando las áreas de todas las caras laterales (trapecios). Otra forma de calcularla es multiplicar la suma de los semiperímetros de las dos bases por la apotema. $$ A_l = (p_B + p_b) \cdot a $$ donde p_B y p_b son los semiperímetros de la base mayor y menor, respectivamente, y "a" es la apotema.

  Demostración. Consideremos una pirámide recta regular con base cuadrada.
  
  El área lateral se obtiene sumando las áreas de las caras laterales. En este caso, todas las caras son trapecios congruentes, cuya área se calcula como $ \frac{(l_1+l_2) \cdot a}{2} $. Este razonamiento, sin embargo, es válido en general, aunque los lados de los trapecios tengan dimensiones distintas. $$ A_l = 4 \cdot \frac{(l_1+l_2) \cdot a}{2} $$ $$ A_l = \frac{(4l_1+4l_2) \cdot a}{2} $$ Aquí, $ P_B = 4l_1 $ representa el perímetro de la base inferior del tronco de pirámide, y $ P_b = 4l_2 $ el perímetro de la base superior. $$ A_l = \frac{(P_B + P_b) \cdot a}{2} $$ Dado que $ p_B = \frac{P_B}{2} $ es el semiperímetro de la base inferior y $ p_b = \frac{P_b}{2} $ el de la base superior, podemos reescribir la fórmula así: $$ A_l = (p_B + p_b) \cdot a $$ Por tanto, el área lateral es igual al producto de la suma de los semiperímetros de las dos bases por la apotema del tronco de pirámide. Como queríamos demostrar.

• Área Total (A_t)
  Es la suma del área lateral y las áreas de las dos bases. $$ A_t = A_B + A_b + A_l $$
• Volumen (V)
  El volumen se calcula con la fórmula: $$ V = \frac{1}{3}h(A_B + A_b + \sqrt{A_B \cdot A_b}) $$ donde \( h \) es la altura del tronco, \( A_B \) es el área de la base mayor y \( A_b \) es el área de la base menor.

  Demostración. El volumen de un tronco de pirámide se obtiene restando el volumen de una pirámide menor y semejante al de una pirámide mayor. Sea $ V_1 $ el volumen de la pirámide mayor con base ABCD, y $ V_2 $ el volumen de la pirámide menor con base A'B'C'D', ambas con vértice en O.
  
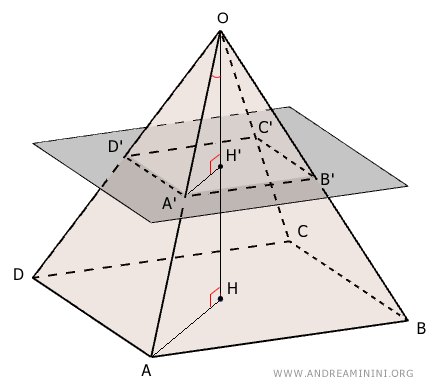
  Sus respectivos volúmenes son: $$ V_1 = \frac{1}{3} ABCD \cdot OH \quad \text{y} \quad V_2 = \frac{1}{3} A'B'C'D' \cdot OH' $$ Así, el volumen del tronco es: $$ V = V_1 - V_2 $$ $$ V = \left( \frac{1}{3} ABCD \cdot OH \right) - \left( \frac{1}{3} A'B'C'D' \cdot OH' \right) $$ Para simplificar, llamemos $ S = ABCD $, $ s = A'B'C'D' $, $ x = OH' $ y $ h + x = OH $. Entonces: $$ V = \frac{1}{3} S \cdot (h + x) - \frac{1}{3} s \cdot x $$ $$ V = \frac{1}{3} S \cdot h + \frac{1}{3} S \cdot x - \frac{1}{3} s \cdot x $$ $$ V = \frac{1}{3} S \cdot h + \frac{1}{3} x \cdot (S - s) $$ Dado que las dos pirámides son semejantes, sus dimensiones lineales y sus alturas son proporcionales. Según el teorema sobre áreas de polígonos semejantes, las secciones paralelas de una pirámide son proporcionales al cuadrado de sus distancias al vértice: $$ S : s = (h + x)^2 : x^2 $$ Extrayendo raíz cuadrada: $$ \sqrt{S:s} = \sqrt{(h + x)^2 : x^2} $$ $$ \sqrt{S} : \sqrt{s} = (h + x) : x $$ Aplicando la propiedad de la diferencia en proporciones, que dice que si $ a:b = c:d $, entonces $ (a - b):b = (c - d):d $: $$ \sqrt{S} - \sqrt{s} : \sqrt{s} = h : x $$ Despejando $ x $ se obtiene: $$ x = \frac{h \sqrt{s}}{ \sqrt{S} - \sqrt{s} } $$ Racionalizando el denominador: $$ x = \frac{h \sqrt{s}}{ \sqrt{S} - \sqrt{s} } \cdot \frac{ \sqrt{S} + \sqrt{s} }{ \sqrt{S} + \sqrt{s} } $$ $$ x = \frac{h \sqrt{s} \cdot ( \sqrt{S} + \sqrt{s} ) }{ (\sqrt{S} - \sqrt{s})( \sqrt{S} + \sqrt{s} ) } $$ $$ x = \frac{h \sqrt{s} \cdot ( \sqrt{S} + \sqrt{s} ) }{ S - s } $$ Sustituyendo esta expresión en la fórmula para $ V $: $$ V = \frac{1}{3} S \cdot h + \frac{1}{3} x \cdot (S - s) $$ $$ V = \frac{1}{3} S \cdot h + \frac{1}{3} \cdot \frac{h \sqrt{s} \cdot ( \sqrt{S} + \sqrt{s} ) }{ S - s } \cdot (S - s) $$ $$ V = \frac{1}{3} S \cdot h + \frac{1}{3} h \cdot \sqrt{s} \cdot ( \sqrt{S} + \sqrt{s} ) $$ $$ V = \frac{1}{3} S \cdot h + \frac{1}{3} h \cdot \sqrt{S \cdot s} + \frac{1}{3} h \cdot s $$ $$ V = \frac{1}{3} h \cdot (S + s + \sqrt{S \cdot s}) $$ Aquí, $ S = A_B $ es el área de la base mayor, y $ s = A_b $ es el área de la base menor del tronco de pirámide. $$ V = \frac{1}{3}h(A_B + A_b + \sqrt{A_B \cdot A_b}) $$

Notas Adicionales

Algunas observaciones y comentarios sobre el tronco de pirámide.

• La sección y la base son polígonos semejantes
  En un tronco de pirámide, la base y cualquier sección paralela a ella son polígonos semejantes.

  Demostración. Tanto la base como la sección se sitúan en planos paralelos, \( \pi \) y \( \pi' \), que cortan las caras laterales de la pirámide original. Esto hace que los lados correspondientes de la base y de la sección sean paralelos: $ AB \parallel A'B' $. Los triángulos \( VAB \) y \( VA'B' \) comparten el vértice \( V \).
  
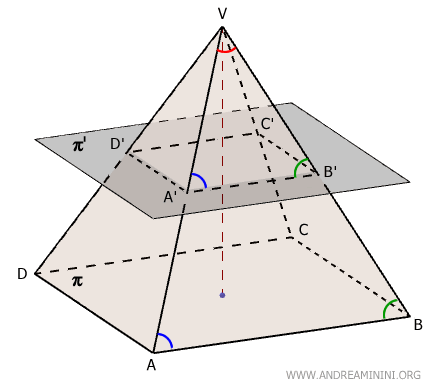
  Los ángulos $ V \hat{A} B $ y $ V \hat{A'} B' $ son congruentes, según el teorema de las rectas paralelas, ya que \( AB \) y \( A'B' \) son paralelos y están cortados por la misma transversal \( VA \). Por la misma razón, los ángulos \( V \hat{B} A \) y \( V \hat{B'} A' \) también son congruentes. En consecuencia, los triángulos \( VAB \) y \( VA'B' \) son semejantes por el criterio de semejanza Ángulo-Ángulo-Ángulo (AAA), al tener todos sus ángulos correspondientes congruentes. $$ VAB \approx VA'B' $$ Esto implica la proporcionalidad entre sus lados correspondientes: $$ AB : A'B' = VB : VB' $$ Lo mismo ocurre con las demás caras laterales: \( VBC \approx VB'C' \), \( VCD \approx VC'D' \) y \( VAD \approx VA'D' \), lo que nos da: $$ BC : B'C' = VB : VB' $$ Por transitividad, se cumple: $$ AB : A'B' = VB : VB' = BC : B'C' $$ Por lo tanto, se concluye: $$ AB : A'B' = BC : B'C' $$ Este razonamiento se extiende a todas las demás caras laterales. Así, no solo los lados correspondientes de la base y de la sección son proporcionales, sino que sus ángulos también son congruentes, al encontrarse en planos que intersectan los mismos diedros de la pirámide.
  
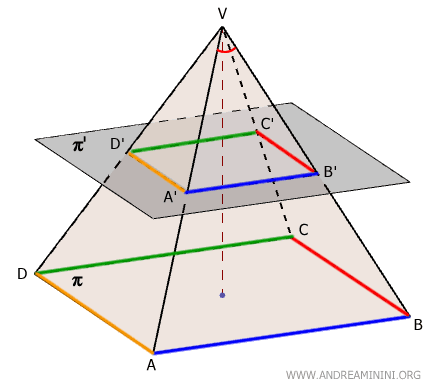
  Por lo tanto, la base y la sección son polígonos semejantes: $$ ABCD \approx A'B'C'D' $$

• Los lados y perímetros se escalan proporcionalmente a la distancia desde el vértice
  Cuando una pirámide se corta mediante un plano paralelo a su base, los lados y el perímetro del polígono resultante son proporcionales a la distancia entre ese plano y el vértice V.

  Demostración. Los triángulos VAH y VA'H' son semejantes por el primer criterio de semejanza, ya que comparten el ángulo en V y ambos contienen un ángulo recto (90°).
  
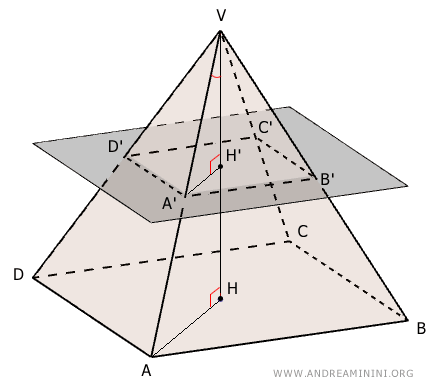
  Como $ VAH \approx VA'H' $, sus lados correspondientes son proporcionales. En particular: $$ \frac{VH}{VH'} = \frac{VA}{VA'} $$ De forma análoga, los triángulos ABV y A'B'V también son semejantes por el mismo criterio. Comparten el ángulo en el vértice V, y los ángulos de la base son congruentes, $ V \hat{A} B \cong V \hat{A'} B' $, según el teorema de las rectas paralelas.
  
  Al ser $ ABV \approx A'B'V $, sus lados correspondientes guardan la misma proporción: $$ \frac{AB}{A'B'} = \frac{VA}{VA'} $$ Por transitividad, dado que $ \frac{VH}{VH'} = \frac{VA}{VA'} $, se concluye que: $$ \frac{AB}{A'B'} = \frac{VH}{VH'} $$ El mismo razonamiento es válido para los demás lados correspondientes de la base y de la sección: $$ \frac{BC}{B'C'} = \frac{VH}{VH'} $$ $$ \frac{CD}{C'D'} = \frac{VH}{VH'} $$ $$ \frac{AD}{A'D'} = \frac{VH}{VH'} $$ Por consiguiente, los perímetros de ambos polígonos también están en la misma proporción: $$ \frac{AB + BC + CD + AD}{A'B' + B'C' + C'D' + A'D'} = \frac{VH}{VH'} $$ Denotando los perímetros como $ 2p $ y $ 2p' $, tenemos: $$ \frac{2p}{2p'} = \frac{VH}{VH'} $$ Así, la razón entre los perímetros coincide con la de cualquier par de lados correspondientes: $$ \frac{2p}{2p'} = \frac{AB}{A'B'} = \frac{BC}{B'C'} = \frac{CD}{C'D'} = \frac{AD}{A'D'} $$

• La razón entre las áreas de la base y de la sección es el cuadrado de la razón de semejanza
  En un tronco de pirámide, la relación entre el área de la base \( S \) y la de la sección \( S' \) es igual al cuadrado de la razón de semejanza. \[ \frac{S}{S'} = \left( \frac{AB}{A'B'} \right)^2 = k^2 \]

  Demostración. La base y la sección de un tronco de pirámide son polígonos semejantes. La razón entre las áreas de dos polígonos semejantes, $ \frac{S}{S'} $, es igual al cuadrado de la razón de semejanza $ k^2 $ (véase la demostración). Por tanto, en un tronco de pirámide, la razón entre el área de la base y la de la sección es el cuadrado de la razón de semejanza $ k $.
  
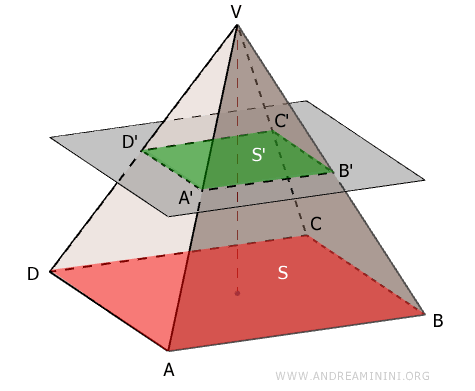
  Por ejemplo, en una pirámide con base cuadrada, el área de la base $ ABCD $ es el cuadrado de uno de sus lados: $ S = (AB)^2 $. Del mismo modo, el área de la sección $ A'B'C'D' $ es $ S' = (A'B')^2 $. Así, la razón entre ambas áreas es: $$ \frac{S}{S'} = \frac{(AB)^2}{(A'B')^2} = \left( \frac{AB}{A'B'} \right)^2 = k^2 $$ donde $ k = \frac{AB}{A'B'} $ es la razón de semejanza entre los dos polígonos. Esta propiedad se cumple para cualquier par de polígonos semejantes, no solo para cuadrados. En dos polígonos semejantes, sus lados correspondientes mantienen la misma razón $ k $, y todas las demás magnitudes lineales - como alturas, diagonales, etc. - varían proporcionalmente en la misma relación.

Y así queda demostrado.