Paraboloide
Un paraboloide es una superficie cuádrica en el espacio tridimensional que se genera a partir de una parábola.
Existen dos tipos principales de paraboloides, según cómo se generen: por rotación o por traslación de una parábola.
- Paraboloide elíptico
Esta superficie se obtiene al rotar una parábola alrededor de su eje de simetría, que normalmente coincide con el eje vertical. El resultado es una forma que recuerda a una copa o a un cuenco profundo. Las secciones horizontales de esta superficie son elipses, mientras que las secciones verticales siguen siendo parábolas. La ecuación general del paraboloide elíptico es: $$ \frac{x^2}{a^2} + \frac{y^2}{b^2} = \frac{z}{c} $$ donde \(a\) y \(b\) son los semiejes de las elipses formadas en los planos horizontales, y \(c\) es un parámetro que determina el grado de apertura del paraboloide.
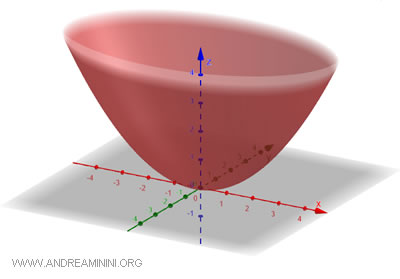
Se denomina “elíptico” porque, al cortar el paraboloide con un plano horizontal, se obtiene como sección una elipse.
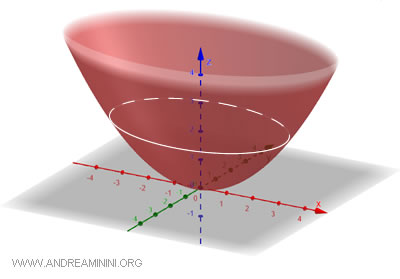
En el caso particular en que \(a = b\), la ecuación se reduce a la de un paraboloide de revolución: $$ x^2 + y^2 = 2pz $$ donde \(p\) es un parámetro relacionado con la apertura de la parábola generadora.

Un ejemplo muy representativo es la antena parabólica, que aprovecha la forma del paraboloide para captar y concentrar señales procedentes del espacio. El paraboloide de revolución resulta especialmente eficaz porque refleja los rayos paralelos hacia un único punto focal, permitiendo concentrar gran cantidad de energía o información. Esta propiedad óptica es fundamental en el diseño de antenas, reflectores y telescopios.
- Paraboloide hiperbólico
Esta superficie se genera al trasladar una parábola a lo largo de una dirección no paralela a su eje de simetría. El resultado es una figura cuyas secciones horizontales son hipérbolas, mientras que las secciones verticales siguen siendo parábolas. La ecuación general del paraboloide hiperbólico es: $$ \frac{x^2}{a^2} - \frac{y^2}{b^2} = \frac{z}{c} $$ donde \(a\) y \(b\) determinan la forma y la extensión de la hipérbola en los cortes horizontales, y \(c\) controla la apertura de la superficie.
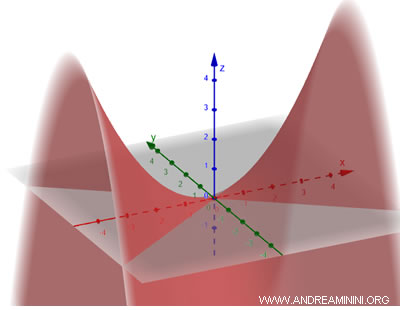
Se denomina “hiperbólico” porque al seccionar la superficie con un plano horizontal se obtiene una hipérbola.
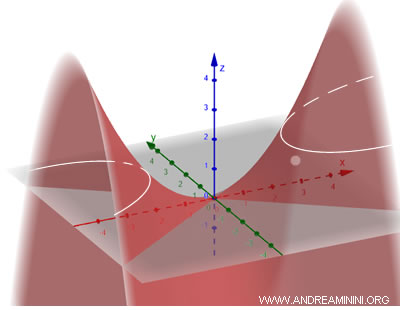
Una aplicación destacada de los paraboloides hiperbólicos se encuentra en la arquitectura, donde se utilizan para diseñar cubiertas curvas que distribuyen el peso de manera eficiente, combinando resistencia estructural con una estética llamativa.
En ambos casos, las secciones verticales son parábolas, lo que justifica el nombre genérico de “paraboloides”.
En resumen, aunque ambos tipos se originan a partir de una parábola, sus formas geométricas y aplicaciones prácticas son muy distintas.
Y así sucesivamente.