Principio de Cavalieri

Dos sólidos tienen el mismo volumen si, para cualquier plano paralelo a una dirección dada (habitualmente horizontal), el área de la sección obtenida al cortar el primer sólido coincide con la del segundo.

Este principio es especialmente útil para analizar sólidos cuyo volumen resulta complicado de calcular mediante fórmulas habituales.

Si logro demostrar que cada sección transversal de un sólido coincide en área con la correspondiente del otro, puedo concluir que se trata de sólidos equivalentes en volumen, aunque sus formas generales sean muy distintas.

No es necesario que los sólidos sean idénticos ni que guarden ninguna simetría particular.

Ejemplo. Imagina dos pilas de hojas perfectamente rectangulares, idénticas en número y dimensiones. Si todas las hojas son iguales, las pilas son congruentes: mismo volumen, misma forma y misma altura. Pero si desplazo las hojas lateralmente en una de las pilas, creando una forma inclinada (como una pila ladeada), la intuición sugiere que el volumen sigue siendo el mismo. Mismo número de capas, misma altura: se ocupa exactamente el mismo espacio.

Esta idea, tan sencilla como revolucionaria, fue introducida por Bonaventura Cavalieri en el siglo XVII. Desde entonces, se la conoce como el Principio de Cavalieri.

Una Limitación del Principio de Cavalieri

El Principio de Cavalieri establece una condición suficiente, pero no necesaria, para la equivalencia de volúmenes.

Si las secciones transversales son iguales a cualquier altura, los volúmenes de los sólidos también lo son.

Sin embargo, la inversa no siempre es cierta: dos sólidos pueden tener el mismo volumen sin cumplir las condiciones del Principio de Cavalieri.

Ejemplo. Dos sólidos pueden encerrar el mismo volumen y, aun así, presentar secciones transversales diferentes a la misma altura. Es decir, aunque ocupen el mismo espacio, no hay manera de alinearlos de modo que cada corte horizontal coincida. Por ejemplo, los dos sólidos que aparecen más abajo tienen el mismo volumen, pero no cumplen con los requisitos del Principio de Cavalieri.

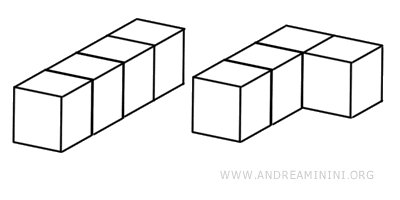
Esto pone de manifiesto una limitación importante: el principio no caracteriza de forma completa la equivalencia volumétrica. Más bien, ofrece un criterio útil, pero parcial.

En esencia, es un método parcial que durante mucho tiempo se consideró exhaustivo. El enfoque de Cavalieri pasa por alto la complejidad espacial total de los sólidos, reduciendo cuerpos tridimensionales a una sucesión de secciones bidimensionales.

Es algo así como afirmar que dos novelas son iguales solo porque una frase cualquiera en ambas tenga el mismo número de palabras.

Nota. Aun así, en el contexto histórico de Cavalieri, la idea supuso un verdadero avance, sobre todo porque en aquella época no existía un marco analítico riguroso para el cálculo de volúmenes. En el árido panorama matemático del siglo XVII, el Principio de Cavalieri representó una auténtica revolución. Sus limitaciones solo se evidenciaron más tarde, con el desarrollo de herramientas más potentes, como el cálculo integral y la topología.

Observaciones Adicionales

Algunas notas y reflexiones adicionales sobre el Principio de Cavalieri:

• Cálculo Integral
  El Principio de Cavalieri puede verse como un antecedente geométrico del cálculo integral: comparar secciones transversales es análogo a sumar áreas infinitesimales, tal como hacemos en las integrales definidas. Su “Geometría de los Indivisibles” anticipa la idea de suma continua sobre la que se basa el cálculo integral.
• Versión Bidimensional
  Dos figuras planas tienen la misma superficie si, para cualquier recta en una dirección fija, las longitudes de los segmentos obtenidos al cortar ambas figuras son iguales.

Y así sucesivamente.