Elipsoide

Un elipsoide es una figura geométrica tridimensional que puede visualizarse como una esfera estirada o achatada.

Dicho de otro modo, es una superficie suave y cerrada, parecida a una esfera, pero con proporciones distintas a lo largo de los ejes x, y y z.

Se genera al rotar una elipse alrededor de uno de sus ejes de simetría.

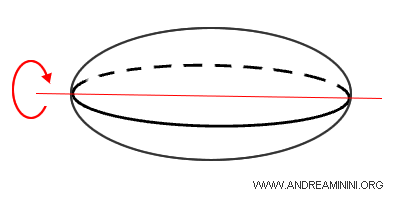
Una elipse es una curva similar a un círculo, pero con dos ejes de longitud diferente: uno mayor y otro menor.

Al girar una elipse, se obtiene una figura con tres dimensiones: altura, anchura y profundidad.

Esto implica que cualquier corte del elipsoide en uno de los planos coordenados da lugar a una elipse.

Ecuación del elipsoide

Desde el punto de vista matemático, la ecuación general de un elipsoide es:

$$ \frac{x^2}{a^2} + \frac{y^2}{b^2} + \frac{z^2}{c^2} = 1 $$

En esta expresión, \(x\), \(y\) y \(z\) son las coordenadas de los puntos que pertenecen a la superficie del elipsoide en el espacio tridimensional.

Las letras \(a\), \(b\) y \(c\) representan las longitudes de los tres semiejes, que determinan la forma y la orientación del elipsoide.

Estos semiejes cumplen un papel análogo al radio en la esfera, pero no necesariamente son iguales entre sí. La ecuación recoge precisamente esta variabilidad.

Un ejemplo concreto

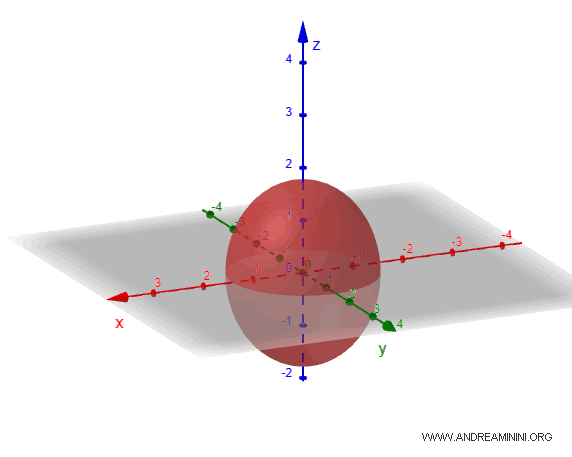
Supongamos un elipsoide cuyos semiejes son $a=2$, $b=1$ y $c=1$.

Su ecuación se escribe así:

$$ \frac{x^2}{2^2} + \frac{y^2}{1} + \frac{z^2}{1} = 1 $$

$$ \frac{x^2}{4} + y^2 + z^2 = 1 $$

Al representar gráficamente esta figura, el elipsoide aparece como una esfera alargada en una dirección y comprimida en otra.

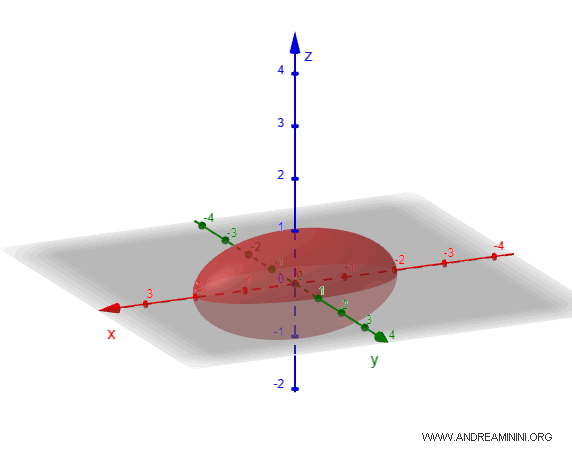
Tipos de elipsoides

Existen distintos tipos de elipsoides, según cómo se relacionan entre sí las longitudes de sus semiejes:

• Elipsoide esférico
  Si los tres semiejes \(a\), \(b\) y \(c\) son iguales, el elipsoide es en realidad una esfera. En este caso, la simetría es total en todas las direcciones y cualquier plano que pase por el centro corta la figura en un círculo perfecto.
  
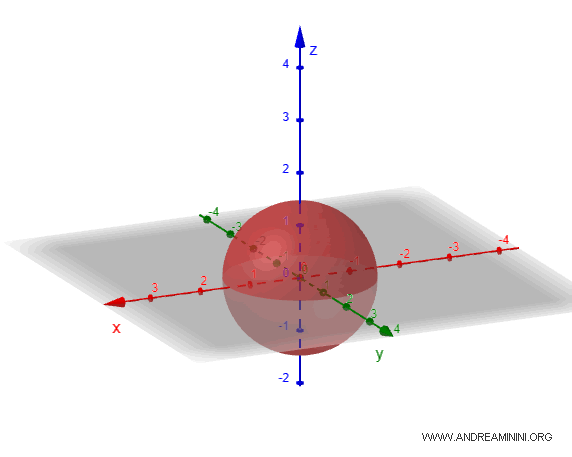
• Elipsoide oblato
  Este tipo de elipsoide se presenta cuando dos de los semiejes (por ejemplo, \(a\) y \(b\)) son iguales y el tercero (\(c\)) es más corto. El resultado es una figura achatada en los extremos, parecida a un disco. Un ejemplo real es la Tierra, que debido a su rotación presenta un ligero achatamiento en los polos.
  
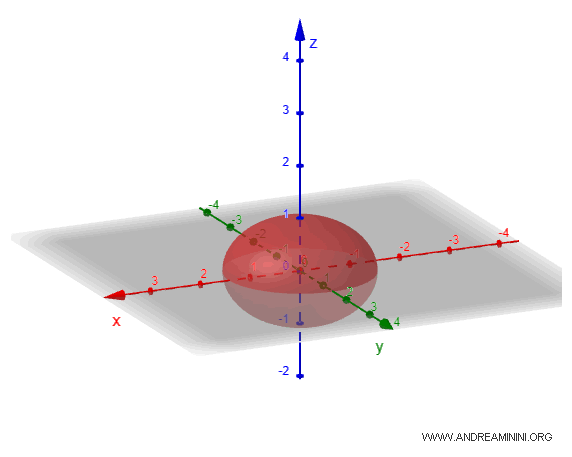
• Elipsoide prolato
  En este caso, dos semiejes son iguales y el tercero es más largo (por ejemplo, \(c > a = b\)). El resultado es una figura alargada a lo largo de un eje, semejante a una pelota de rugby. Es como si una esfera se hubiera estirado en una dirección concreta.
  

Nota. Los elipsoides no son meros objetos abstractos: tienen múltiples aplicaciones prácticas. En astronomía, por ejemplo, se utilizan para describir la forma de cuerpos celestes como planetas o estrellas que, debido a su rotación, no son perfectamente esféricos. La Tierra, por ejemplo, se modela como un elipsoide oblato.

En resumen, el elipsoide es una generalización tridimensional de la esfera que permite representar con precisión formas naturales y artificiales que encontramos tanto en nuestro planeta como en el universo.