Ángulos Diedros

Un ángulo diedro es una figura geométrica definida por la intersección de dos semiplanos, denominados “caras”, que comparten una recta común llamada “arista”.

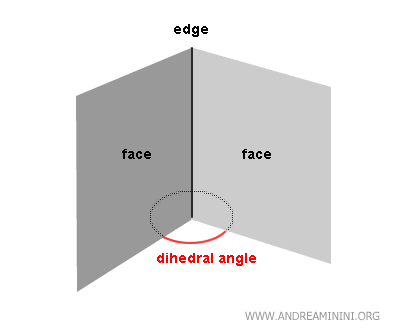
Este concepto es fundamental en la geometría tridimensional.

Los dos semiplanos dividen el espacio en dos regiones distintas, cada una de las cuales constituye un ángulo diedro.

Las caras de un ángulo diedro delimitan su superficie o frontera.

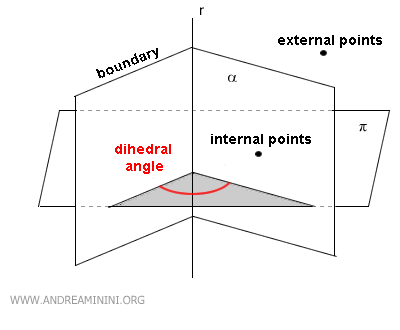
Los puntos situados en el interior del diedro, pero que no pertenecen a su superficie, se denominan puntos interiores.

El ángulo formado entre los dos semiplanos, medido en un plano π, se conoce como ángulo diedro. Dicho ángulo puede ser cóncavo o convexo.

Si el plano π es perpendicular a la arista (r), se habla de la sección normal del ángulo diedro.

Diferencia entre un diedro y un poliedro: Un diedro es una región del espacio definida por dos semiplanos que comparten una recta y forman un ángulo. Un poliedro, en cambio, es un sólido delimitado por superficies planas llamadas “caras”. Las rectas en las que se encuentran dos caras se denominan “aristas”, y los puntos donde confluyen tres o más aristas se llaman “vértices”. Ejemplos de poliedros son el cubo, la pirámide y el prisma. En esencia, mientras un diedro se define por dos planos y un ángulo, un poliedro es un sólido tridimensional compuesto por múltiples caras planas.

Secciones de un Diedro

La sección de un diedro es el ángulo resultante de la intersección del diedro con un plano que corta su arista.

En términos sencillos, la sección es la proyección del ángulo diedro sobre un plano determinado.

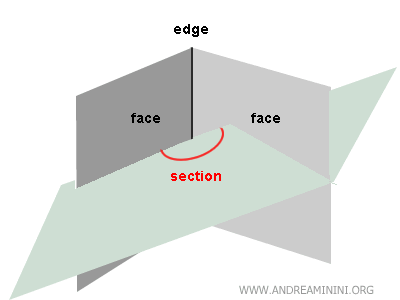
Esto evidencia que el equivalente del diedro en la geometría plana es simplemente un ángulo.

En particular, se habla de sección normal cuando el plano que corta el diedro es perpendicular a la arista.

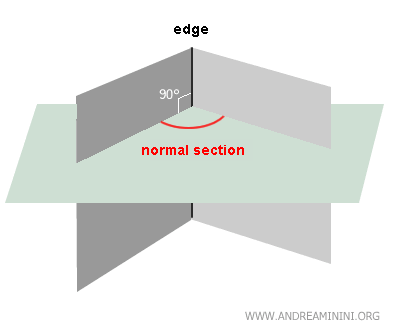
Todas las propiedades de un diedro se derivan de su sección normal.

Por ejemplo, la sección normal permite determinar si el diedro es convexo o cóncavo:

• Diedro Convexo
  Un diedro convexo no contiene las prolongaciones de sus caras. Su sección normal mide menos de 180°.
• Diedro Cóncavo
  Un diedro cóncavo sí incluye las prolongaciones de sus caras. Su sección normal mide más de 180°.

Nota: Cuando la sección normal mide exactamente 180°, es decir, un ángulo llano, el diedro está formado por dos planos que se intersecan perpendicularmente. En este caso, la sección corresponde a la recta de intersección de dichos planos, y el diedro se denomina diedro llano (180°). Si las caras coinciden, se habla de diedro completo si abarca todo el espacio, o de diedro nulo si no contiene puntos interiores.

Según el ángulo de su sección, un diedro también puede clasificarse como recto (90°), obtuso (>90°) o agudo (<90°).

• Diedro Recto
  Un diedro recto posee una sección normal de 90°, representando exactamente la mitad de un diedro llano.
• Diedro Agudo
  Los diedros cuya sección normal mide menos de 90° se denominan diedros agudos.
• Diedro Obtuso
  Los diedros cuya sección normal mide más de 90° pero menos de 180° se denominan diedros obtusos.
  

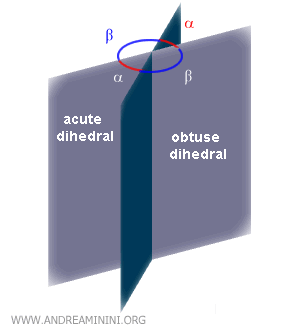
En función de sus secciones normales, dos diedros pueden ser complementarios, suplementarios o explementarios.

• Diedros Complementarios
  Dos diedros son complementarios cuando la suma de sus ángulos equivale a un diedro recto (90°).
• Diedros Suplementarios
  Dos diedros son suplementarios cuando la suma de sus ángulos equivale a un diedro llano (180°).
• Diedros Explementarios
  Dos diedros son explementarios cuando la suma de sus ángulos equivale a un diedro completo (360°).

Ejemplo: Los diedros α y β son suplementarios porque la suma de sus ángulos es igual a un diedro llano (180°).

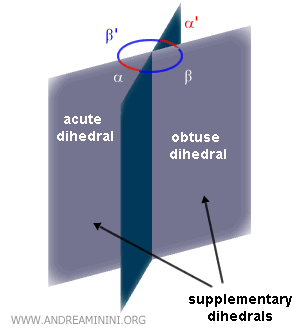
Congruencia de Diedros

Dos diedros son congruentes cuando poseen la misma sección normal.

En otras palabras, dos diedros son congruentes si y solo si pueden superponerse mediante movimientos rígidos.

En cualquier caso, los diedros congruentes presentan secciones normales congruentes.

Ejemplo: Los diedros α y β son congruentes porque comparten la misma sección normal (90°).

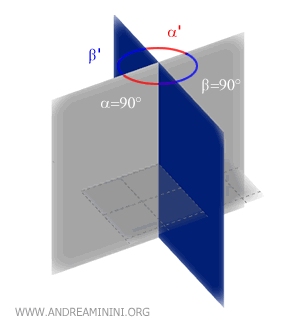
Diedros Opuestos en la Arista

Dos diedros se denominan diedros opuestos si comparten una misma arista y las caras de uno son prolongaciones de las caras del otro.

Por ejemplo, los ángulos α y α' son opuestos respecto a la arista.

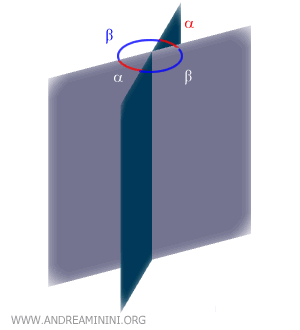
Los diedros opuestos en la arista siempre son congruentes.

Esto es análogo a lo que ocurre con los ángulos opuestos por el vértice en geometría plana.

Diedros Consecutivos y Adyacentes

Los diedros pueden clasificarse como consecutivos o adyacentes según su disposición espacial:

• Diedros Consecutivos
  Dos diedros son consecutivos si comparten la misma arista y una de sus caras.
• Diedros Adyacentes
  Dos diedros son adyacentes si, además de ser consecutivos, sus caras no comunes son semiplanos opuestos.

  Nota: Dos diedros adyacentes son también suplementarios, ya que la suma de sus ángulos diedros es de 180°. Por ejemplo, los diedros α y β son consecutivos porque comparten la misma arista y una cara. Además, son adyacentes porque sus otras caras son opuestas.
  
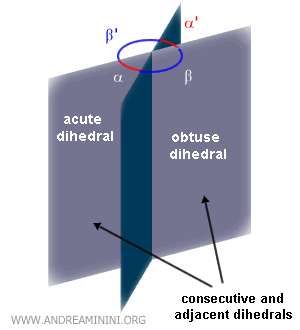
  De manera similar, los pares α y β', α' y β', y α' y β son adyacentes por las mismas razones. En cambio, el par de diedros α y α' no se considera consecutivo.

Notas Adicionales

A continuación, algunos datos adicionales sobre los ángulos diedros:

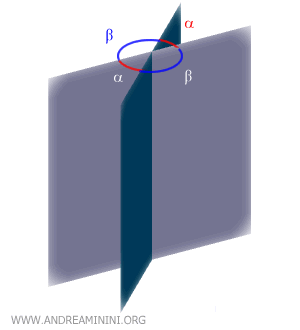
• Dos planos no paralelos generan cuatro diedros, formando dos pares de diedros opuestos respecto a la arista.
• Dos planos son perpendiculares si forman cuatro diedros rectos
  Como los ángulos diedros opuestos respecto a la arista son congruentes, basta que uno de ellos sea recto para que los demás también lo sean.
  
• Dos semiplanos que comparten una arista dividen el espacio en dos diedros explementarios, ya que la suma de sus ángulos diedros es de 360°. Si ambos diedros no son llanos, uno tendrá un ángulo menor a 180° (convexo) y el otro mayor a 180° (cóncavo).
  
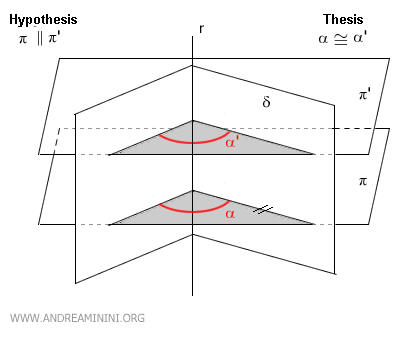
• Las secciones paralelas de un diedro son congruentes
  Las secciones paralelas π y π' de un diedro δ presentan el mismo ángulo diedro α ≅ α'.
  
• La suma de dos diedros consecutivos da lugar a un nuevo diedro con la misma arista y caras no comunes.

Y así sucesivamente.