Cubo

Un cubo es un paralelepípedo rectangular (poliedro) formado por seis caras cuadradas idénticas, todas con ángulos rectos y aristas iguales.

Cada una de las seis caras del cubo es un cuadrado perfecto. 

Por ello, el cubo también recibe el nombre de hexaedro regular.

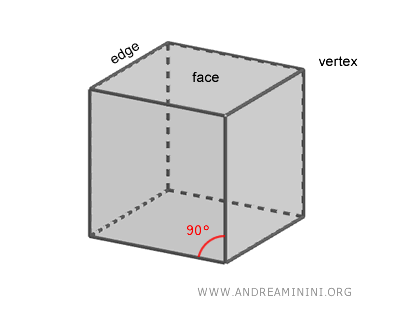
La palabra “hexaedro” proviene del griego, donde “hexa” significa “seis” y “hedron” significa “cara” o “base”. El término “regular” indica que cada cara del cubo es un polígono regular, es decir, que todos sus lados y ángulos son iguales.

Desde el punto de vista geométrico, un cubo es un caso particular de prisma rectangular en el que las tres dimensiones - longitud (l), ancho (w) y altura (h) - son exactamente iguales.

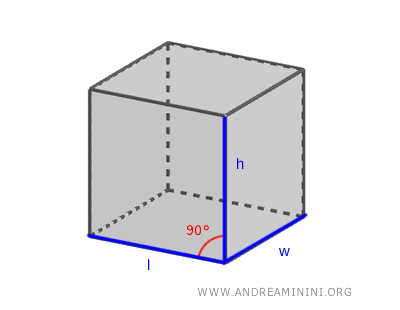
Cada cara del cubo está unida a otras cuatro a través de sus aristas, lo que da un total de 12 aristas iguales.

Además, el cubo tiene 8 vértices, en cada uno de los cuales confluyen tres aristas y se encuentran tres caras mutuamente perpendiculares.

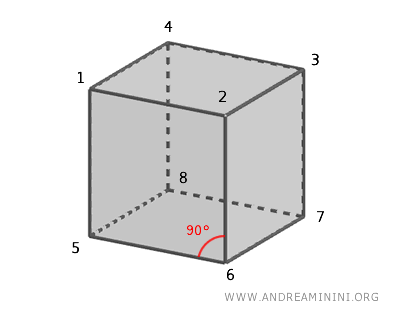
Esta característica otorga al cubo una notable estabilidad y simetría. Su forma es el paradigma del equilibrio, lo que lo convierte en uno de los sólidos más estudiados en geometría. Como uno de los cinco sólidos platónicos, simboliza armonía, simetría y perfección.

Fórmulas

Las fórmulas para calcular el volumen y el área superficial de un cubo son especialmente simples gracias a su estructura regular.

• Volumen
  El volumen se calcula elevando al cubo la longitud de una arista: $$ V = l^3 $$

  Nota. El cubo es un caso particular de prisma rectangular en el que todas las aristas tienen la misma longitud. Por ello, su fórmula de volumen es simplemente un caso particular de la fórmula general para el volumen de un prisma rectangular.

• Área Total
  El área superficial total se obtiene sumando las áreas de sus seis caras: $$ A = 6l^2 $$
• Área de una Cara
  El área de cada cara del cubo es la de un cuadrado cuyo lado mide lo mismo que la arista del cubo (l): $$ A_B = l^2 $$

  Nota. De esta relación se deduce la fórmula del área total. Dado que el cubo posee seis caras, todas de la misma área (A_B = l²), se concluye que el área total del cubo es A = 6A_B = 6l².

• Diagonal
  La diagonal del cubo se obtiene multiplicando la longitud de una arista por la raíz cuadrada de tres: $$ d = l \cdot \sqrt{3} $$

Así, conociendo la longitud de una arista (l), es posible calcular fácilmente el volumen, el área superficial total y el área de cada una de las caras del cubo.

Simetría del Cubo

Gracias a su forma, el cubo cuenta con numerosos ejes de simetría y conserva su apariencia sin importar el eje alrededor del cual se lo gire.

Los ejes de simetría son:

• Las tres rectas que unen los centros de caras opuestas, que actúan como ejes de rotación.
  
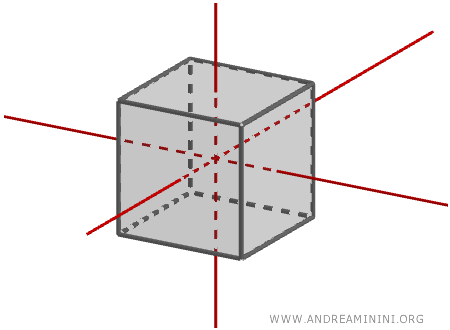
• Las seis rectas que conectan los puntos medios de aristas opuestas, que también son ejes de simetría.
  
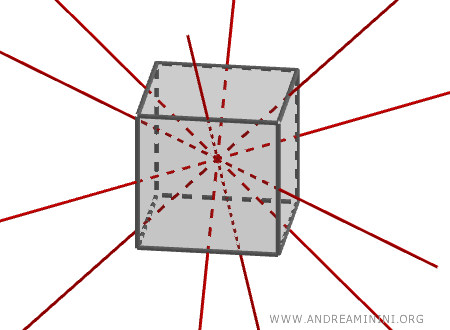
• Las cuatro diagonales que enlazan un vértice con el vértice opuesto situado en la cara contraria, las cuales también constituyen ejes de simetría.
  

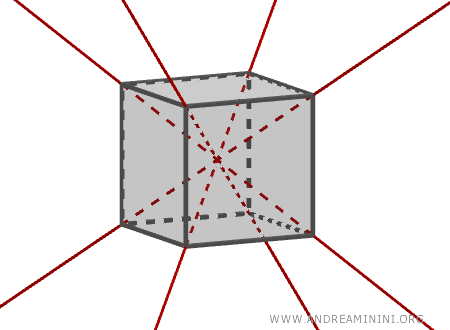
Las diagonales del cubo se cruzan en un único punto, denominado centro de simetría del cubo, que coincide con el centro de la esfera circunscrita que pasa por todos sus vértices.

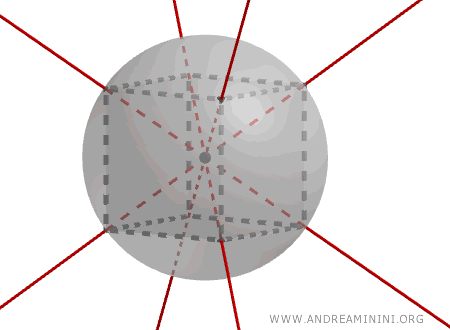
Por ello, el cubo es un objeto de gran interés en matemáticas, especialmente en el campo de la teoría de grupos.

Notas Adicionales

Algunos datos y curiosidades adicionales sobre el cubo:

• El cubo es el único paralelepípedo cuyas tres dimensiones son exactamente iguales.
• Entre todos los paralelepípedos rectangulares con la misma superficie total, el cubo es el que posee el mayor volumen.
• En matemáticas, “elevar al cubo” significa elevar un número a la tercera potencia
  Esta denominación procede de la fórmula del volumen del cubo, que implica elevar la longitud de la arista (l) a la tercera potencia: $$ V = l^3 $$ Por eso, “elevar al cubo” un número significa multiplicarlo por sí mismo tres veces.
• Todas sus caras no solo son idénticas en forma, sino también en tamaño, siendo cada una un reflejo especular de las demás.

Y así sucesivamente.