Prisma Recto

Un prisma recto es un sólido geométrico que cuenta con dos bases paralelas y congruentes, y cuyas caras laterales son rectángulos.

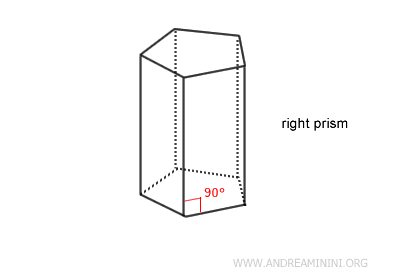
Las bases pueden tener cualquier forma poligonal, aunque lo más habitual es que sean polígonos regulares, como triángulos, cuadrados, pentágonos, entre otros. Ambas bases tienen la misma forma y tamaño y se encuentran en planos paralelos.

Las caras laterales son siempre rectangulares, y su número coincide con el número de lados del polígono que forma la base.

Un prisma recto es un caso particular de prisma en el cual las caras laterales son perpendiculares a las bases. Esto implica que los ángulos entre las bases y las caras laterales son todos ángulos rectos (90 grados). Gracias a su forma simple y regular, el prisma recto encuentra numerosas aplicaciones prácticas, especialmente en arquitectura, ingeniería y diseño.

La altura del prisma es la distancia perpendicular entre los planos que contienen sus dos bases.

Fórmulas del Prisma Recto

A continuación, se presentan las principales fórmulas para calcular las magnitudes de un prisma recto:

• Área Lateral
  El área lateral de un prisma recto se obtiene multiplicando el perímetro de la base (P) por la altura (h) del prisma: $$ A_L = P \cdot h $$
• Área Total
  El área superficial total es la suma del área lateral (A_L) y el doble del área de la base (2A_B). Es decir, es la superficie total de todas las caras del prisma, incluidas las bases. $$ A = A_L + 2A_B $$
• Volumen
  El volumen de un prisma recto se obtiene multiplicando el área de una de sus bases (A_B) por la altura (h) del prisma: $$ V = A_B \cdot h $$

Un Ejemplo Práctico

Veamos el caso de un prisma recto cuya base es un pentágono regular, en el que cada lado mide 3 cm y la altura del prisma es de 10 cm.

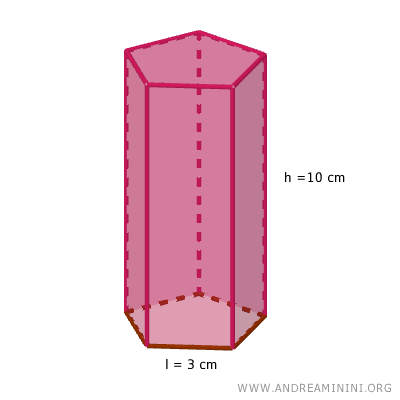
Queremos calcular el área total y el volumen del prisma.

Primero, vamos a determinar el perímetro de la base (P_B) y el área de la base (A_B). Como ambas bases son congruentes, basta con analizar una de ellas.

La base de este prisma es un pentágono regular en el que cada lado mide 3 cm.

Por tanto, el perímetro de la base (P_B) es la suma de sus cinco lados, es decir, 15 cm.

$$ P_B = 3 \cdot 5 = 15 \ cm $$

Para hallar el área del pentágono, necesitamos calcular su apotema. Para un pentágono regular, se utiliza un valor aproximado de 0.688 multiplicado por la longitud del lado, es decir:

$$ a = 3 \cdot 0.688 = 2.064 $$

Con la apotema (aproximadamente a=2.064 cm), calculamos el área de la base (A_B) multiplicando la apotema por el semiperímetro de la base (p = P_B/2):

$$ A_B = a \cdot \frac{P_B}{2} $$

$$ A_B = 2.064 \cdot \frac{15}{2} = 15.48 \ cm^2 $$

Con estos datos, podemos calcular el área total y el volumen del prisma recto.

El área lateral (A_L) del prisma se obtiene multiplicando el perímetro de la base (P_B = 15 cm) por la altura (h = 10 cm):

$$ A_L = P_B \cdot h $$

$$ A_L = 15 \ cm \cdot 10 \ cm = 150 \ cm^2 $$

El área total (A) del prisma se calcula sumando el área lateral (A_L) y el doble del área de la base (2A_B):

$$ A = A_L + 2A_B $$

$$ A = 150 \ cm^2 + 2 \cdot 15.48 \ cm^2 $$

$$ A = 150 \ cm^2 + 30.96 \ cm^2 $$

Por lo tanto, el área total del prisma es aproximadamente 180.96 cm².

$$ A = 180.96 \ cm^2 $$

Finalmente, el volumen del prisma se calcula multiplicando el área de la base (A_B = 15.48 cm²) por la altura (h = 10 cm):

$$ V = A_B \cdot h $$

$$ V = 15.48 \ cm^2 \cdot 10 \ cm $$

En consecuencia, el volumen del prisma es aproximadamente 154.8 cm³.

$$ V = 154.8 \ cm^3 $$

¡Así de sencillo se resuelve este tipo de ejercicio!