Paralelepípedo

Un paralelepípedo es un tipo de prisma cuyas bases son paralelogramos.

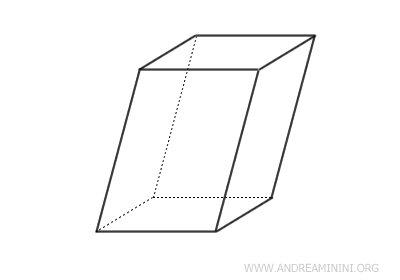
Es un sólido que cuenta con 6 caras, todas ellas paralelogramos, además de 12 aristas y 8 vértices.

Un paralelepípedo presenta las siguientes propiedades:

• Sus caras opuestas son paralelas y congruentes.
• Las aristas opuestas son paralelas y tienen la misma longitud.
• Los vértices opuestos se encuentran alineados sobre rectas paralelas.

Las longitudes de las tres aristas que concurren en un mismo vértice se denominan las dimensiones del paralelepípedo.

El estudio de los paralelepípedos se remonta a la Antigua Grecia, donde matemáticos como Euclides describieron sus propiedades y características.

Tipos de Paralelepípedos

Existen distintos tipos de paralelepípedos, según la forma y orientación de sus caras.

• Paralelepípedos rectos
  Tienen caras laterales que son rectángulos.
  
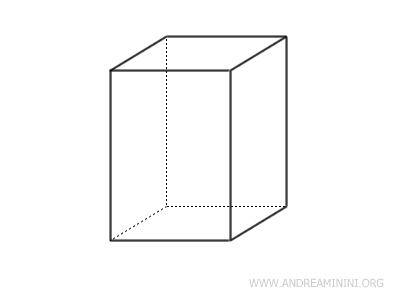
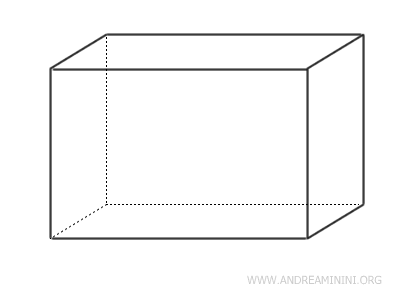
• Paralelepípedos rectangulares
  Sus bases son rectángulos, lo que hace que todas sus caras sean rectangulares.
  
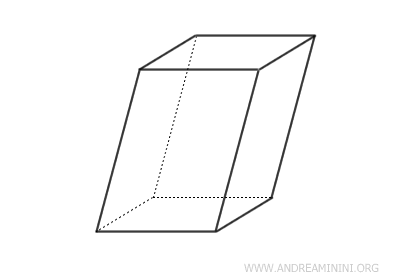
• Paralelepípedos oblicuos
  En estos, las caras laterales no son rectángulos; al menos una de ellas es un rombo u otro tipo de paralelogramo.
  

En geometría espacial, son especialmente relevantes los siguientes tipos concretos de paralelepípedos:

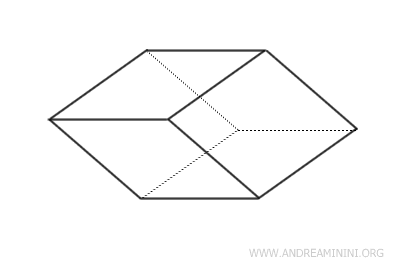
• Romboedro
  Es un paralelepípedo cuyas seis caras son rombos congruentes.
  
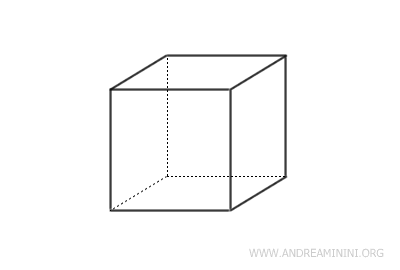
• Cubo
  Es un paralelepípedo cuyas seis caras son cuadrados congruentes. Constituye un caso particular tanto de paralelepípedo rectangular como de romboedro.
  

Fórmulas para Paralelepípedos

Al igual que cualquier prisma, el volumen V de un paralelepípedo se calcula multiplicando el área de una de sus bases A_B por su altura h.

$$ V = A_B \cdot h $$

Paralelepípedo Rectangular

En un paralelepípedo rectangular, cuyas dimensiones de la base son l (longitud), w (ancho) y h (altura):

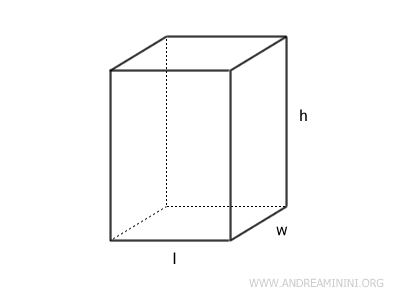
El volumen V se obtiene multiplicando sus tres dimensiones:

$$ V = l \cdot w \cdot h $$

Aquí, A_B = l · w corresponde al área de la base.

$$ V = A_B \cdot h $$

Esto se debe a que un prisma rectangular es un caso particular de prisma.

El área lateral S_L de un paralelepípedo rectangular se calcula multiplicando el perímetro de la base, 2(w + l), por la altura h.

$$ S_L = 2 \cdot (w + l) \cdot h $$

Donde P_B = 2(w + l) es el perímetro de la base.

$$ S_L = P_B \cdot h $$

Otra manera de hallar el área lateral es sumando las áreas de las caras laterales:

$$ S_L = 2 \cdot (w \cdot h + l \cdot h) $$

El área total S_T de un paralelepípedo es la suma de las áreas de sus seis caras. Puede expresarse como el área lateral S_L = 2(w + l)h más el doble del área de la base 2lw:

$$ S_T = 2(w + l)h + 2lw $$

$$ S_T = 2lw + 2lh + 2wh $$

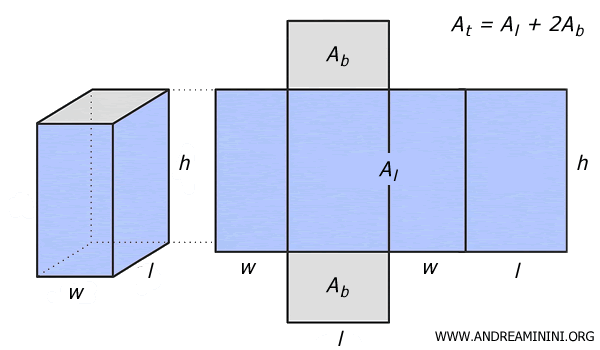
Nota. Conviene recordar que el área total $ A_t $ es la suma del área lateral $ A_l $ y el doble del área de la base $ A_b $. Al observar el desarrollo plano del prisma rectangular, se comprende fácilmente la lógica de la fórmula.

La diagonal (d) de un paralelepípedo rectangular se obtiene calculando la raíz cuadrada de la suma de los cuadrados de sus dimensiones:

$$ d = \sqrt{l^2 + w^2 + h^2} $$

Paralelepípedo Rectangular

Un paralelepípedo rectangular es un sólido tridimensional en el que tanto las bases como las caras laterales son rectángulos.

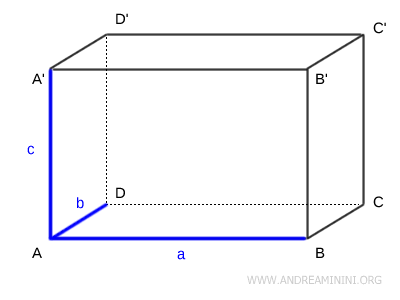
Las dimensiones de un paralelepípedo son las longitudes de las tres aristas que se unen en un vértice común, y se representan como \( a, b, c \).

Nota. El concepto de dimensiones es especialmente útil y claro en el caso del paralelepípedo rectangular, pues sus aristas son perpendiculares entre sí, lo que facilita tanto su representación como sus cálculos. Por ejemplo, las diagonales pueden determinarse aplicando el teorema de Pitágoras. En un paralelepípedo genérico, aunque las dimensiones siguen existiendo, los cálculos relacionados con aristas y diagonales son más complejos, ya que las aristas no necesariamente son perpendiculares y es necesario considerar los ángulos entre ellas.

La diagonal del paralelepípedo, denotada como \( d \), es el segmento que une dos vértices opuestos.

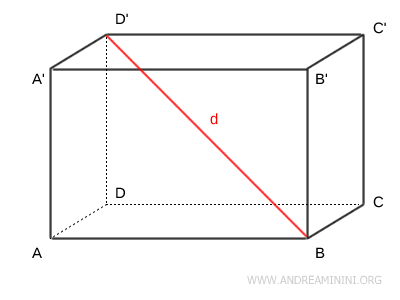
En un paralelepípedo rectangular, todas las diagonales espaciales son congruentes.

La fórmula para calcular la longitud de la diagonal espacial tiene en cuenta las tres dimensiones del sólido:

\[ d = \sqrt{a^2 + b^2 + c^2} \]

Esta ecuación expresa la máxima distancia posible entre dos vértices opuestos.

Demostración. Para deducir esta fórmula, consideremos la diagonal espacial \( d \) del paralelepípedo y la diagonal \( d_b \) de la base rectangular ABCD.

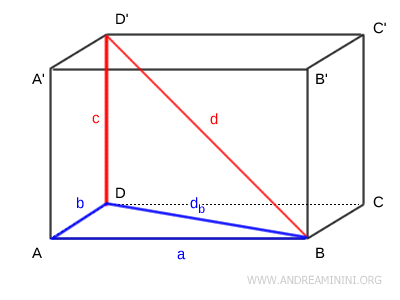
Aplicamos el teorema de Pitágoras al triángulo rectángulo \( ABD \), formado por dos lados contiguos de la base, y obtenemos la longitud de la diagonal de la base \( d_b \): \[ d_b^2 = a^2 + b^2 \] \[ d_b = \sqrt{a^2 + b^2} \] Después, volvemos a aplicar el teorema de Pitágoras al triángulo rectángulo \( DBD' \), en el que la diagonal de la base \( d_b \) y la altura \( c \) son los catetos: \[ d^2 = d_b^2 + c^2 \] Sustituyendo \( d_b^2 = a^2 + b^2 \) obtenemos: \[ d^2 = (a^2 + b^2) + c^2 \] \[ d = \sqrt{a^2 + b^2 + c^2} \] Por tanto, la fórmula para la diagonal espacial de un paralelepípedo rectangular es: \[ d = \sqrt{a^2 + b^2 + c^2} \] .

Observaciones y Notas

A continuación, algunas observaciones adicionales sobre los paralelepípedos:

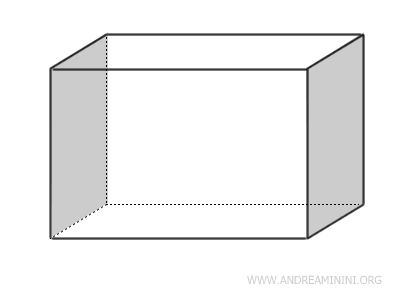
• Las caras opuestas de un paralelepípedo son congruentes y paralelas
  Las superficies opuestas de un paralelepípedo, es decir, aquellas que no comparten vértices, son congruentes y se encuentran en planos paralelos.
  
• Las diagonales de un paralelepípedo se cruzan en un único punto, dividiéndose mutuamente en segmentos congruentes.
  

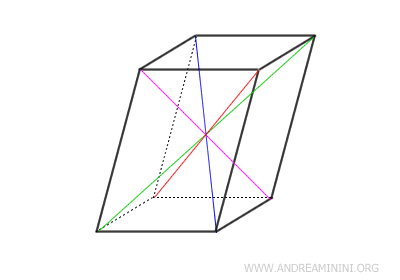
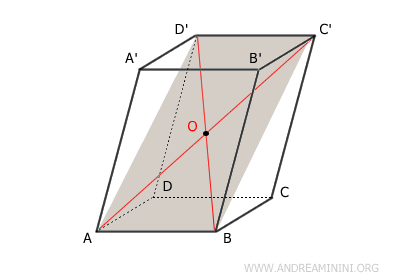
  Demostración. En este paralelepípedo, el cuadrilátero $ ABC'D' $ forma un paralelogramo, pues sus lados opuestos son congruentes y paralelos. En consecuencia, sus diagonales $ AC' $ y $ BD' $ se intersectan en su punto medio $ O $, lo cual implica que $ OA \cong OC' \cong OB \cong OD' $.
  
  De manera similar, el cuadrilátero $ BCD'A' $ también es un paralelogramo, ya que cumple la misma propiedad de tener lados opuestos congruentes y paralelos. Así, sus diagonales $ BD' $ y $ A'C' $ se intersectan en su punto medio $ O $, dividiéndose en segmentos iguales: $ OB \cong OC \cong OA' \cong OD' $. El punto $ O $ coincide con el del caso anterior $ ABC'D' $, dado que el segmento $ BD' $ es común a ambas configuraciones.
  
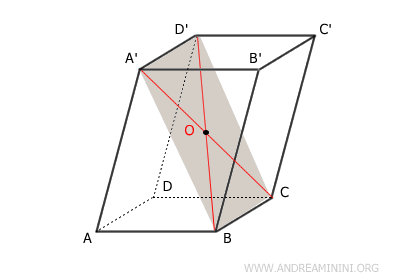
  Aplicando el mismo razonamiento a las restantes diagonales del paralelepípedo, se concluye que todas ellas se intersectan en un mismo punto $ O $, dividiéndose en dos segmentos congruentes.

• En un paralelepípedo rectangular, todas las diagonales espaciales son congruentes.
• Si dos prismas rectangulares tienen bases congruentes $ A_B $, sus volúmenes son directamente proporcionales a sus alturas: $$ \frac{V_1}{V_2} = \frac{A_B \cdot h_1}{A_B \cdot h_2} = \frac{h_1}{h_2} $$ 

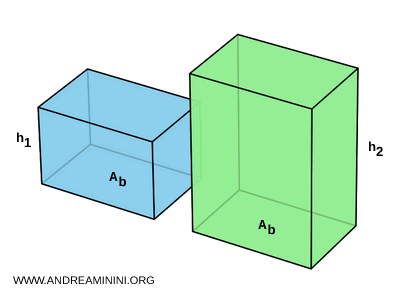
  Demostración. El volumen $ V $ de un prisma rectangular se calcula multiplicando sus tres dimensiones: $$ V = l \cdot w \cdot h $$ Dado que el área de la base es $ A_B = l \cdot w $, se puede expresar como: $$ V = A_B \cdot h $$  Si dos prismas tienen áreas de base idénticas (es decir, bases congruentes) y el mismo volumen, entonces necesariamente deben tener la misma altura: $$ V_1 = V_2 \quad \text{y} \quad A_{B_1} = A_{B_2} \quad \Rightarrow \quad h_1 = h_2 $$ Por el contrario, si tienen igual área de base pero volúmenes distintos, entonces la razón entre sus volúmenes es igual a la razón entre sus alturas: $$ \frac{V_1}{V_2} = \frac{A_B \cdot h_1}{A_B \cdot h_2} = \frac{h_1}{h_2} $$ En síntesis, cuando la base se mantiene constante, el volumen de un prisma rectangular varía de manera proporcional a su altura.

Y así sucesivamente.