Adición y sustracción de sólidos
La geometría sólida estudia las figuras tridimensionales, conocidas como sólidos, y las operaciones que se pueden realizar con ellas. Entre estas operaciones, la unión y la diferencia constituyen herramientas fundamentales para combinar o eliminar volúmenes.
Unión de sólidos
La unión de dos sólidos A y B que no comparten puntos interiores (es decir, que son disjuntos o sólo se tocan en sus bordes) da lugar a un nuevo sólido C formado por todos los puntos que pertenecen a A o a B. $$ A + B = C $$
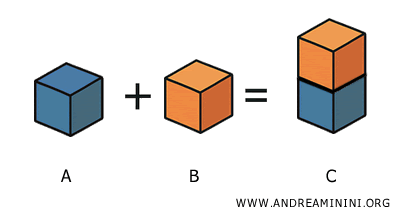
Los sólidos A y B se consideran componentes del sólido resultante C.
La operación de unión cumple con dos propiedades fundamentales:
- Conmutativa: El orden en que se combinan los sólidos no altera el resultado. $$ A + B = B + A = C $$
- Asociativa: Al combinar más de dos sólidos, la forma en que se agrupan no afecta el resultado final. $$ (A + B) + C = A + (B + C) $$
Estas propiedades hacen que la unión sea especialmente útil para descomponer y reconstruir formas complejas, lo cual resulta clave tanto en el cálculo de volúmenes como en procesos de modelado tridimensional.
Ejemplo
Consideremos dos cubos: uno de arista 3 cm y otro de 2 cm, situados próximos entre sí, sin superposición.
Su unión, representada por el sólido C, incluye ambos cubos como partes distintas y separadas.
El volumen total es simplemente la suma de los volúmenes individuales:
\[ V = 3^3 + 2^3 = 27 + 8 = 35\ \text{cm}^3 \]
Diferencia de sólidos
La diferencia entre dos sólidos A y B es el sólido C definido como: $$ C = A - B $$ Es decir, C representa la parte de A que permanece después de sustraer B.
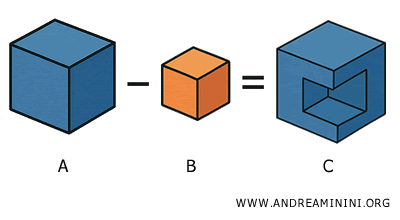
Para que esta operación esté bien definida, el sólido B debe estar contenido total o parcialmente dentro del sólido A.
Ejemplo
Tomemos nuevamente los dos cubos: uno de 3 cm por lado y otro de 2 cm.
En este caso, el cubo más pequeño se encuentra completamente incrustado dentro del mayor, centrado de forma precisa.
El sólido resultante C = A − B es un cubo hueco con una cavidad en el centro. El volumen restante es:
\[ V = 3^3 - 2^3 = 27 - 8 = 19\ \text{cm}^3 \]
Y así sucesivamente.