Ecuaciones de superficies en el espacio

En geometría analítica, una superficie se define como el conjunto de todos los puntos cuyas coordenadas cartesianas $x, y, z$ satisfacen una ecuación de la forma: $$ F(x, y, z) = 0 $$ Esta ecuación determina con exactitud qué puntos pertenecen a la superficie.

La expresión $F(x, y, z) = 0$ permite comprobar si un punto concreto se encuentra sobre la superficie: basta con sustituir las coordenadas $x, y, z$ y verificar si la igualdad se cumple. Además, proporciona información esencial sobre la forma geométrica de la superficie.

Según el tipo de superficie, la ecuación puede ir desde las formas más simples hasta expresiones altamente complejas.

Gracias a la ecuación $F(x, y, z) = 0$, es posible clasificar las superficies en distintas categorías, como planos, cuádricas y otras variedades más generales.

Superficies algebraicas

Si la función $F(x, y, z)$ es un polinomio, la superficie recibe el nombre de superficie algebraica.

Se dice que es de grado n (u orden $n$) cuando el polinomio tiene grado $n$.

Las superficies de primer grado son los planos, definidos por ecuaciones lineales de la forma:

$$ ax + by + cz + d = 0 $$

donde $a, b, c, d$ son constantes reales.

Por ejemplo, la siguiente ecuación representa un plano: $$ 2x - 3y + z + 5 = 0 $$ Esta es la representación del plano en el espacio tridimensional.

Para determinar si un punto pertenece al plano, basta sustituir sus coordenadas en la ecuación y verificar si la igualdad se cumple. Por ejemplo, ¿el punto $(1, -1, 0)$ pertenece al plano? Comprobémoslo: $$2 \cdot 1 - 3 \cdot (-1) + 0 + 5 = 2 + 3 + 5 = 10 \neq 0$$ Como el resultado no es cero, el punto no pertenece al plano.

Las superficies de segundo grado se denominan cuádricas y están definidas por ecuaciones cuadráticas.

Superficies cuadráticas

Las cuádricas son superficies descritas por una ecuación polinómica de segundo grado de la forma general:

$$ ax^2 + by^2 + cz^2 + dxy + exz + fyz + gx + hy + iz + l = 0 $$

Según los valores de los coeficientes, esta ecuación puede describir una gran variedad de superficies, entre ellas:

• elipsoides
• hiperboloides
• paraboloides
• conos
• cilindros

Elipsoide

Un elipsoide es una superficie que generaliza la esfera, obtenida al estirar o comprimir los radios a lo largo de los tres ejes coordenados. Su ecuación canónica es:

$$ \frac{x^2}{a^2} + \frac{y^2}{b^2} + \frac{z^2}{c^2} = 1 $$

Si $a = b = c$, la superficie corresponde a una esfera.

Por ejemplo, la ecuación:

$$ \frac{x^2}{9} + \frac{y^2}{4} + \frac{z^2}{1} = 1 $$

describe un elipsoide con semiejes $a = 3$, $b = 2$ y $c = 1$.

Hiperboloide

Un hiperboloide es una superficie cuádrica que puede tener una sola hoja continua o estar compuesta por dos hojas separadas.

La ecuación de un hiperboloide de una hoja es:

$$ \frac{x^2}{a^2} + \frac{y^2}{b^2} - \frac{z^2}{c^2} = 1 $$

La del hiperboloide de dos hojas es:

$$ - \frac{x^2}{a^2} - \frac{y^2}{b^2} + \frac{z^2}{c^2} = 1 $$

Un ejemplo concreto de hiperboloide de una hoja es: $$ \frac{x^2}{4} + \frac{y^2}{9} - \frac{z^2}{16} = 1 $$ Esta superficie presenta una “cintura” central estrecha que se ensancha hacia arriba y hacia abajo.

Paraboloide

Los paraboloides son superficies que se obtienen al rotar una parábola alrededor de un eje. Pueden clasificarse en paraboloides elípticos e hiperboloidales.

La ecuación de un paraboloide elíptico es:

$$ \frac{x^2}{a^2} + \frac{y^2}{b^2} = 2z $$

La del paraboloide hiperbólico es:

$$ \frac{x^2}{a^2} - \frac{y^2}{b^2} = 2z $$

Por ejemplo, la ecuación: $$ \frac{x^2}{4} + \frac{y^2}{9} = 2z $$ define un paraboloide elíptico.

Cono

Un cono tiene su vértice en el origen y se extiende indefinidamente en ambas direcciones a lo largo de su eje. Su ecuación típica es:

$$ \frac{x^2}{a^2} + \frac{y^2}{b^2} - \frac{z^2}{c^2} = 0 $$

Por ejemplo, esta ecuación define un cono: $$ \frac{x^2}{4} + \frac{y^2}{9} - \frac{z^2}{16} = 0 $$

Cilindro

Una superficie cilíndrica se genera al desplazar una curva directriz a lo largo de una dirección fija mediante rectas llamadas generatrices.

Cuando la ecuación de la superficie depende solo de dos variables (por ejemplo, $x^2 - y - 1 = 0$), sus soluciones forman una curva plana (en el plano Oxy, por ejemplo), conocida como directriz.

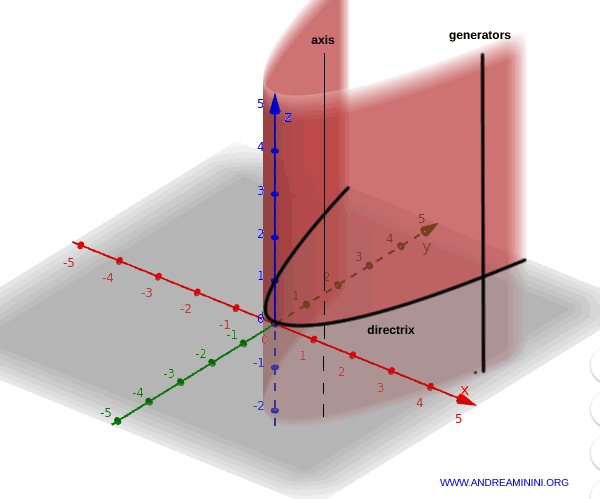
Al trasladar esta curva a lo largo del eje libre (por ejemplo, el eje z), se obtiene toda la superficie cilíndrica.

La forma de la directriz determina el tipo de cilindro:

• si es parabólica, el cilindro es parabólico
• si es elíptica, el cilindro es elíptico
• si es circular, el cilindro es circular
• si es hiperbólica, el cilindro es hiperbólico

La ecuación de un cilindro circular se escribe habitualmente como:

$$ x^2 + y^2 + a x + b y + c = 0 $$

Obsérvese que no interviene la variable $z$, ya que la superficie se prolonga indefinidamente a lo largo del eje $z$.

Esta ecuación representa un cilindro circular siempre que se cumpla la condición:

$$ \frac{a^2}{4} + \frac{b^2}{4} - c \ge 0 $$

Es decir, esto garantiza que la directriz en el plano xy es realmente una circunferencia.

Lo mismo se aplica en los planos xz e yz, cuando la ecuación involucra $x$ y $z$ o $y$ y $z$, respectivamente.

Ejemplo. Un ejemplo práctico de un cilindro circular en el espacio tridimensional es: $$ \frac{x^2}{4} + \frac{y^2}{4} = 1 $$ Esta ecuación describe una superficie cilíndrica circular.

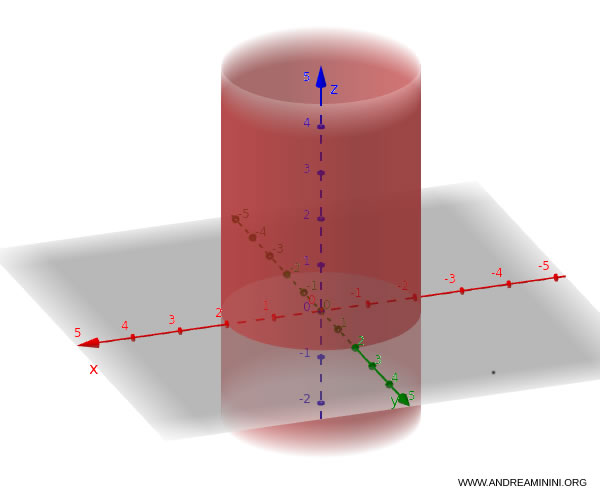
La ecuación de un cilindro elíptico es:

$$ \frac{x^2}{a^2} + \frac{y^2}{b^2} = 1 $$

Cuando se cumple que $a = b$, el cilindro tiene sección circular.

Ejemplo. Este es un ejemplo de cilindro en el espacio tridimensional: $$ \frac{x^2}{4} + \frac{y^2}{9} = 1 $$ La sección transversal en este caso es una elipse.

La ecuación de un cilindro hiperbólico es:

$$ \frac{x^2}{a^2} - \frac{y^2}{b^2} = 1 $$

Esta relación se cumple para todos los valores de $z$, definiendo una superficie cilíndrica hiperbólica cuyo eje es paralelo al eje $z$.

Ejemplo. He aquí un cilindro hiperbólico: $$ \frac{x^2}{2} - \frac{y^2}{4} = 3 $$ En este caso, la directriz es una hipérbola en el plano xy y las generatrices son paralelas al eje $y$.

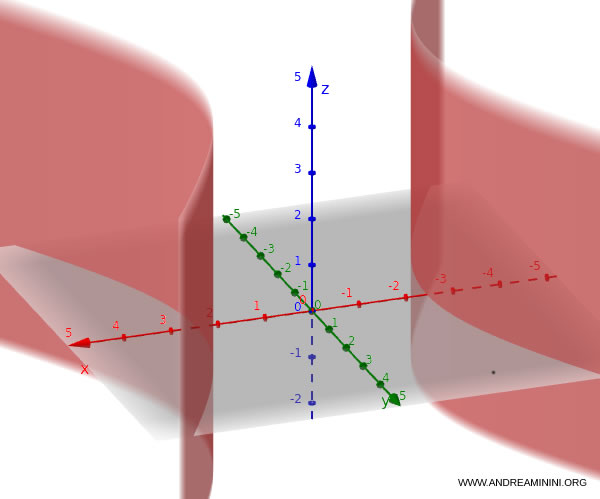
La ecuación de un cilindro parabólico tiene la forma:

$$ y = k x^2 $$

Si esta relación se mantiene para todo $z$, describe una superficie cilíndrica parabólica con eje paralelo al eje $z$.

Ejemplo. Consideremos la directriz: $$ y = x^2. $$ La superficie resultante es $ y = x^2, \quad z \in \mathbb{R} $.

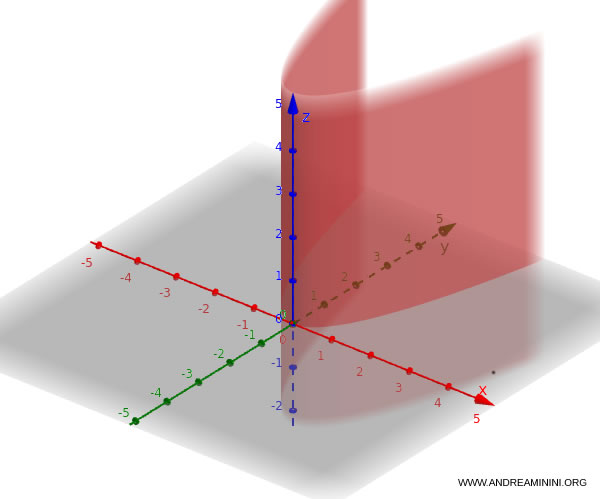
Esta ecuación puede escribirse de forma implícita como: $$ y - x^2 = 0 $$ o bien $$ x - y^2 = 0 $$. Si la ecuación involucra $x$ y $z$, se obtiene: $$ z = x^2 $$, lo que representa un cilindro parabólico con eje paralelo a $y$.

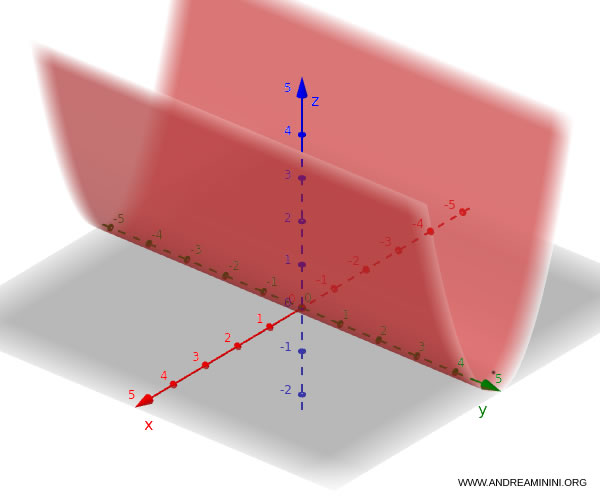
Si, en cambio, involucra $y$ y $z$: $$ z = y^2 $$ En tal caso, la superficie es un cilindro parabólico con eje paralelo a $x$.

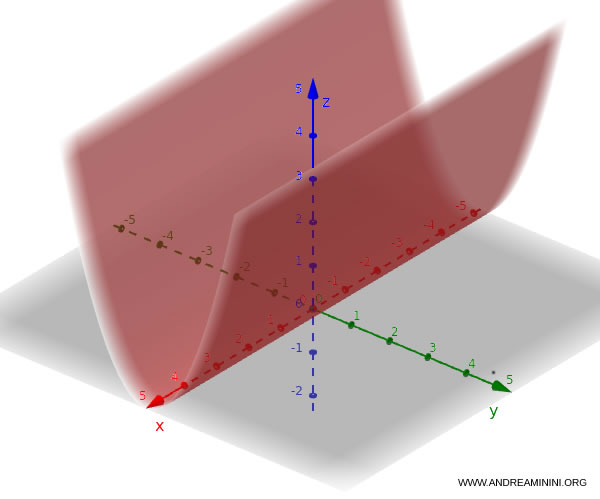
Estos ejemplos muestran cómo las distintas superficies cuádricas pueden describirse mediante ecuaciones de segundo grado, cada una con su propia forma característica en el espacio tridimensional.  

Secciones planas de superficies

Para estudiar las curvas generadas al cortar una superficie con un plano, podemos imponer restricciones fijando un valor concreto para $z$ o $y$.

Por ejemplo, consideremos el elipsoide:

$$ \frac{x^2}{9} + \frac{y^2}{4} + \frac{z^2}{1} = 1 $$

Si establecemos $z = 0$, obtenemos:

$$ \frac{x^2}{9} + \frac{y^2}{4} = 1 $$

El resultado es una elipse situada en el plano $xy$, que constituye una sección plana del elipsoide.

Curva como intersección de dos superficies

Una curva en el espacio tridimensional puede definirse como la intersección de dos superficies: $$ \begin{cases} F(x, y, z) = 0 \\ G(x, y, z) = 0 \end{cases} $$

Es decir, el conjunto de puntos cuyas coordenadas $(x, y, z)$ satisfacen simultáneamente ambas ecuaciones suele describir una curva en el espacio.

La descripción analítica de esta curva queda dada por el sistema:

$$
\begin{cases}
F(x, y, z) = 0 \\
G(x, y, z) = 0
\end{cases}
$$

Esta representación se conoce como forma implícita de la curva, ya que no expresa las variables $x$, $y$ y $z$ en función de un parámetro.

Ejemplo

Veamos el sistema definido por las siguientes dos superficies:

$$
\begin{cases}
x^{2} - y + z - 1 = 0 \\
x^{2} + 2y + z - 1 = 0
\end{cases}
$$

La intersección de estas superficies da lugar a una curva compuesta por los puntos que satisfacen ambas ecuaciones al mismo tiempo.

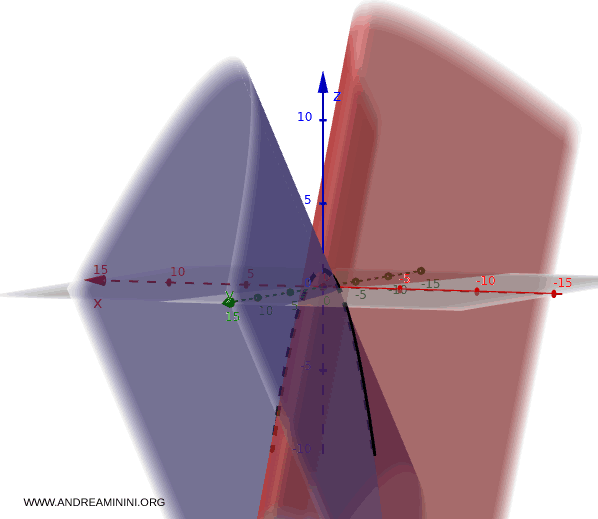
En muchos casos, resulta útil parametrizar la curva para facilitar su análisis o representación gráfica.

Introduzcamos un parámetro $t$ y definamos:

$$ x = t $$

A continuación, igualamos las dos ecuaciones para despejar $y$:

$$ x^{2} - y + z - 1 = x^{2} + 2y + z - 1 $$

Restando ambos lados, obtenemos:

$$ x^{2} - y + z - 1 - \bigl(x^{2} + 2y + z - 1\bigr) = 0 $$

Lo cual se simplifica como:

$$ -3y = 0 $$

Por lo tanto:

$$ y = 0 $$

Ahora sustituimos $x = t$ y $y = 0$ en una de las ecuaciones originales para hallar $z$:

$$ x^{2} + 2y + z - 1 = 0 $$

$$ t^2 + 2 \cdot 0 + z - 1 = 0 $$

De donde se obtiene:

$$ z = 1 - t^2 $$

Así, la curva de intersección puede describirse mediante las siguientes ecuaciones paramétricas:

$$
\begin{cases}
x = t \\
y = 0 \\
z = 1 - t^{2}
\end{cases}
$$

Esto permite visualizar fácilmente la curva en GeoGebra mediante el comando Curve:

Curve(t, 0, 1 - t^2, t, -5, 5)

Y así sucesivamente.