Ecuación cartesiana de una esfera

Una esfera es el conjunto de puntos P en el espacio tridimensional (R3) que se encuentran a una misma distancia de un punto fijo C, denominado centro de la esfera. A esta distancia constante se le llama radio, r. $$ d(C,P)=r $$

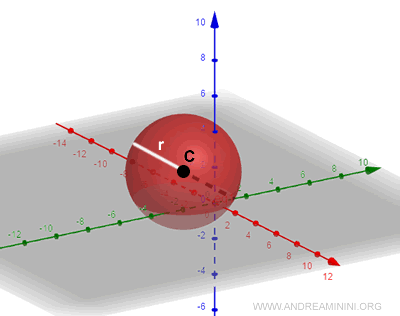
• Puntos interiores
  Son los puntos cuya distancia al centro es mayor que cero y menor que el radio. $$ 0 < d(C,P) < r $$
• Puntos exteriores
  Se denominan puntos exteriores aquellos cuya distancia al centro es mayor que el radio. $$ d(C,P) > r $$

Nota. Si la distancia es cero, la esfera se reduce al punto C.

Cómo obtener la ecuación cartesiana de una esfera

Podemos deducir la ecuación cartesiana de una esfera a partir de su definición.

$$ d(C,P)=r $$

Establecemos un sistema de referencia cartesiano RC(O;i,j,k).

El centro C es un punto con coordenadas \( x_0, y_0, z_0 \) en el espacio euclídeo.

$$ C = \begin{pmatrix} x_0 \\ y_0 \\ z_0 \end{pmatrix} $$

Consideramos ahora un punto genérico P sobre la superficie de la esfera:

$$ P = \begin{pmatrix} x \\ y \\ z \end{pmatrix} $$

La distancia entre estos dos puntos se calcula mediante la fórmula:

$$ d(C,P) = \sqrt{(x-x_0)^2+(y-y_0)^2+(z-z_0)^2} $$

Como esta distancia es igual al radio, se cumple:

$$ d(C,P) = r $$

De ahí obtenemos:

$$ \sqrt{(x-x_0)^2+(y-y_0)^2+(z-z_0)^2} = r $$

Elevando ambos miembros al cuadrado:

$$ (x-x_0)^2+(y-y_0)^2+(z-z_0)^2 = r^2 $$

Esta es la forma estándar de la ecuación cartesiana de una esfera:

$$ (x-x_0)^2+(y-y_0)^2+(z-z_0)^2 = r^2 $$

Cada esfera está completamente determinada por una ecuación de esta forma.

Podemos desarrollar esta expresión para obtener la forma general:

$$ (x-x_0)^2+(y-y_0)^2+(z-z_0)^2 = r^2 $$

Al expandir cada término:

$$ (x^2 - 2xx_0 + x_0^2) + (y^2 - 2yy_0 + y_0^2) + (z^2 - 2zz_0 + z_0^2) = r^2 $$

Lo que equivale a:

$$ x^2 - 2xx_0 + x_0^2 + y^2 - 2yy_0 + y_0^2 + z^2 - 2zz_0 + z_0^2 - r^2 = 0 $$

Reagrupamos los coeficientes de la siguiente manera:

$$ \begin{pmatrix} a = -2x_0 \\ b = -2y_0 \\ c = -2z_0 \\ d = x_0^2 + y_0^2 + z_0^2 - r^2 \end{pmatrix} $$

Nota. Este sistema también permite calcular el centro y el radio a partir de los coeficientes. Tras unas simples manipulaciones algebraicas se obtiene: $$ \begin{pmatrix} x_0 = - \frac{a}{2} \\ y_0 = - \frac{b}{2} \\ z_0 = - \frac{c}{2} \\ r = \sqrt{x_0^2 + y_0^2 + z_0^2 - d} \end{pmatrix} $$ La expresión bajo la raíz debe ser mayor o igual que cero. Por tanto, para que la ecuación represente una esfera, debe cumplirse: $$ x_0^2 + y_0^2 + z_0^2 - d \geq 0 $$ o, en función de los coeficientes: $$ \left( \frac{a}{2} \right)^2 + \left( \frac{b}{2} \right)^2 + \left( \frac{c}{2} \right)^2 - d \geq 0 $$.

Sustituyendo los coeficientes en la ecuación obtenemos la forma general de la ecuación cartesiana de una esfera:

$$ x^2 + y^2 + z^2 + ax + by + cz + d = 0 $$

Como se ha indicado, esta ecuación es única para cada esfera.

Un ejemplo práctico

Analicemos si la siguiente ecuación representa una esfera:

$$ x^2 + y^2 + z^2 + 3x + 2y - 3z - 4 = 0 $$

Identificamos los coeficientes:

$$ \begin{pmatrix} a = 3 \\ b = 2 \\ c = -3 \\ d = -4 \end{pmatrix} $$

Será una esfera si se verifica la siguiente condición:

$$ \left( \frac{a}{2} \right)^2 + \left( \frac{b}{2} \right)^2 + \left( \frac{c}{2} \right)^2 - d \geq 0 $$

Sustituyendo los valores:

$$ \left( \frac{3}{2} \right)^2 + \left( \frac{2}{2} \right)^2 + \left( \frac{-3}{2} \right)^2 - (-4) \geq 0 $$

$$ \frac{9}{4} + 1 + \frac{9}{4} + 4 \geq 0 $$

$$ \frac{9}{2} + 5 \geq 0 $$

$$ \frac{19}{2} \geq 0 $$

La condición se cumple, por lo tanto representa una esfera.

Cálculo del centro y el radio de la esfera

Una vez confirmamos que se trata de una esfera, podemos determinar las coordenadas de su centro C ( x₀, y₀, z₀ ) y su radio r.

Usamos el siguiente sistema:

$$ \begin{pmatrix} a = -2x_0 \\ b = -2y_0 \\ c = -2z_0 \\ d = x_0^2 + y_0^2 + z_0^2 - r^2 \end{pmatrix} $$

Con los valores dados:

$$ \begin{pmatrix} 3 = -2x_0 \\ 2 = -2y_0 \\ -3 = -2z_0 \\ -4 = x_0^2 + y_0^2 + z_0^2 - r^2 \end{pmatrix} $$

De ahí obtenemos:

$$ x_0 = - \frac{3}{2}, \, y_0 = -1, \, z_0 = \frac{3}{2} $$

Y el radio:

$$ r^2 = x_0^2 + y_0^2 + z_0^2 + 4 $$

Por tanto:

$$ r = \sqrt{ \left( - \frac{3}{2} \right)^2 + (-1)^2 + \left( \frac{3}{2} \right)^2 + 4 } $$

$$ r = \sqrt{ \frac{9}{4} + 1 + \frac{9}{4} + 4 } $$

$$ r = \sqrt{ \frac{9}{2} + 5 } $$

$$ r \approx 3.08 $$

Así que el centro tiene coordenadas:

$$ C = \begin{pmatrix} - \frac{3}{2} \\ -1 \\ \frac{3}{2} \end{pmatrix} $$

Y el radio es:

$$ r = 3.08 $$

Nota. He verificado las coordenadas del centro y el valor del radio utilizando Geogebra, y los cálculos son correctos.

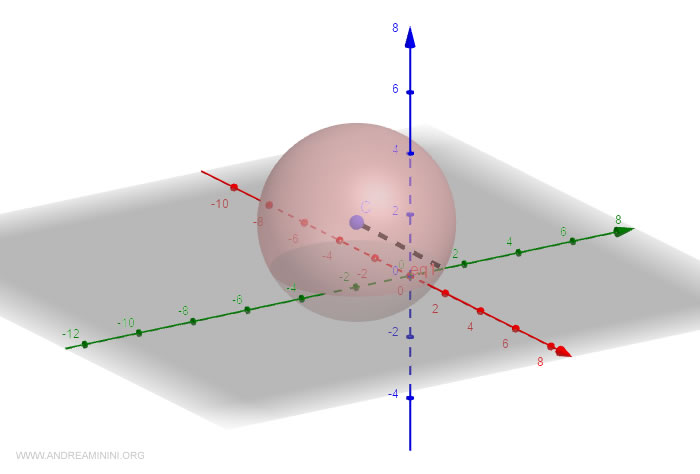
Y así sucesivamente