Puntos dentro y fuera de una esfera

Con respecto a una esfera, los puntos en el espacio se pueden clasificar de la siguiente manera:

• Puntos interiores: si la distancia entre el punto P y el centro C de la esfera es menor que el radio r. $$ d(C,P) < r $$
• Puntos exteriores: si la distancia entre el punto P y el centro C es mayor que el radio. $$ d(C,P) > r $$

Un ejemplo práctico

Consideremos una esfera cuyo centro se encuentra en las coordenadas (x, y, z) del espacio y que tiene un radio igual a dos unidades.

$$ C = \begin{pmatrix} 5 \\ 3 \\ 2 \end{pmatrix} $$

$$ r = 2 $$

Tomemos ahora un punto P en el espacio con las siguientes coordenadas:

$$ P = \begin{pmatrix} 1 \\ 2 \\ 3 \end{pmatrix} $$

Queremos saber si este punto se encuentra dentro o fuera de la esfera.

Para ello, calculamos la distancia entre los puntos C y P.

$$ ||\overrightarrow{CP}|| = \sqrt{(5-1)^2+(3-2)^2+(2-3)^2} $$

$$ ||\overrightarrow{CP}|| = \sqrt{(4)^2+(1)^2+(1)^2} $$

$$ ||\overrightarrow{CP}|| = \sqrt{18} \approx 4.24 $$

La distancia entre C y P es aproximadamente 4.24, valor que supera el radio de la esfera, r = 2.

$$ d(C,P)=4.24 > r = 2 $$

Por lo tanto, el punto P se encuentra fuera de la esfera.

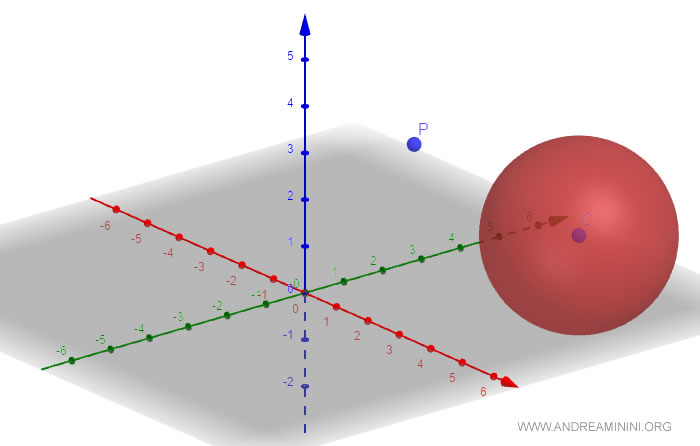
Así es como se determina la posición relativa de un punto respecto a una esfera.