Plano secante, tangente o externo a una esfera

Un plano α puede intersectar una esfera, ser tangente a ella o situarse completamente en el exterior, dependiendo de la distancia entre el plano y el centro C de la esfera de radio r. $$ d(C,\alpha) < r \:\: secante \\ d(C,\alpha) = r \:\: tangente \\ d(C,\alpha) > r \:\: externo $$

Ejemplo práctico

Consideremos una esfera cuyo centro C tiene coordenadas (x, y, z) en el espacio, y cuyo radio es igual a 2.

$$ C = \begin{pmatrix} 5 \\ 3 \\ 2 \end{pmatrix} $$

$$ r = 2 $$

Definimos ahora un plano α en el espacio con la siguiente ecuación:

$$ \alpha : -3x + 2y + z = 0 $$

Queremos determinar si este plano corta la esfera, la roza en un solo punto (es tangente) o no la toca en absoluto.

Para ello, calculamos la distancia entre el centro de la esfera y el plano.

$$ d(C,\alpha) = \frac{|ax_0 + by_0 + cz_0 + d|}{\sqrt{a^2 + b^2 + c^2}} $$

Sustituimos los valores a partir de la ecuación del plano:

$$ d(C,\alpha) = \frac{|-3x_0 + 2y_0 + z_0 + d|}{\sqrt{(-3)^2 + 2^2 + 1^2}} $$

$$ d(C,\alpha) = \frac{|-3(5) + 2(3) + 1(2) + 0|}{\sqrt{9 + 4 + 1}} $$

$$ d(C,\alpha) = \frac{|-15 + 6 + 2|}{\sqrt{14}} $$

$$ d(C,\alpha) = \frac{7}{\sqrt{14}} \approx 1.87 $$

La distancia entre el centro de la esfera y el plano es menor que el radio:

$$ d(C,\alpha) \approx 1.87 < r = 2 $$

En consecuencia, el plano α es secante a la esfera, es decir, la intersecta en una circunferencia.

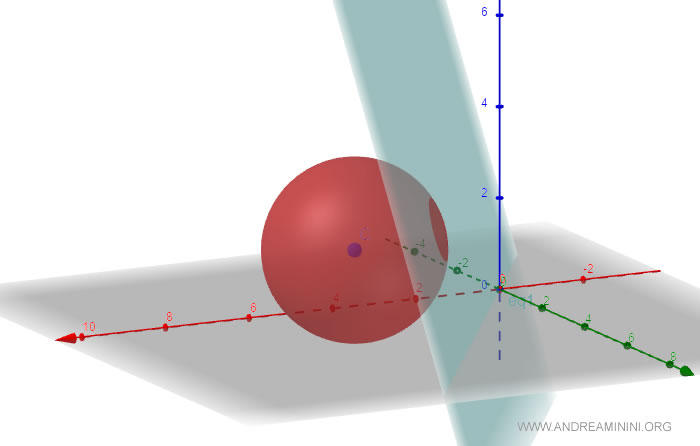
Este es el procedimiento que permite determinar la posición relativa de un plano respecto a una esfera.