Esfera

Una esfera es un sólido generado al girar un semicírculo 360 grados en torno a su diámetro. Se trata de una figura geométrica perfectamente simétrica.

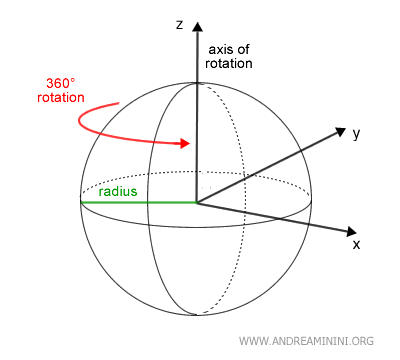
La rotación completa del semicírculo da origen a la superficie esférica.

El punto C representa el centro de la esfera y se encuentra a igual distancia de todos los puntos sobre la superficie.

El radio del semicírculo se convierte en el radio de la esfera, es decir, la distancia desde el centro hasta cualquier punto de su superficie.

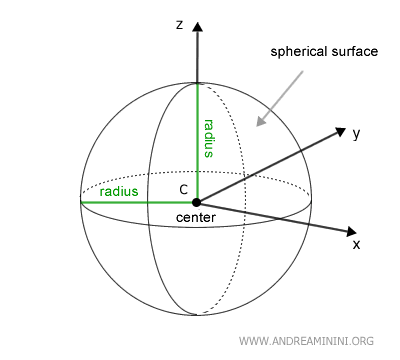
Otra forma de entender la esfera es como un sólido de revolución generado al girar un círculo 180 grados. El resultado geométrico es idéntico.

También puede definirse como el conjunto de todos los puntos del espacio cuya distancia a un punto fijo, llamado centro (C), es menor o igual a un valor determinado.

En cambio, la superficie esférica corresponde al conjunto de puntos situados a una distancia exacta del centro, igual al radio de la esfera.

El estudio de las esferas se remonta a la antigüedad. Filósofos y matemáticos griegos como Platón y Arquímedes investigaron sus propiedades con gran profundidad. En particular, Arquímedes descubrió fórmulas fundamentales para calcular su volumen y área superficial. La esfera también ha tenido un fuerte valor simbólico en la filosofía y la cosmología. Para los griegos, representaba la perfección, la armonía y el universo. Este simbolismo está presente en muchas otras culturas, donde la esfera se asocia a menudo con la totalidad y el infinito.

Fórmulas

A continuación, se presentan las fórmulas esenciales para calcular las propiedades de una esfera:

• Área superficial
  El área de la superficie de una esfera se calcula con la fórmula $$ 4πr^2 $$, donde \( r \) es el radio.

  Nota. El área superficial de una esfera equivale a cuatro veces el área de su círculo máximo. $$ 4 \cdot \pi r^2 $$
  
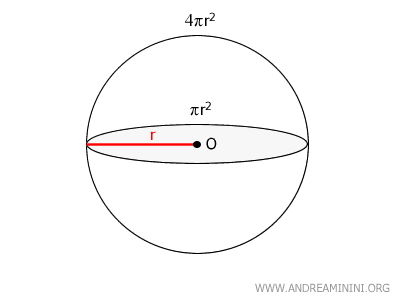
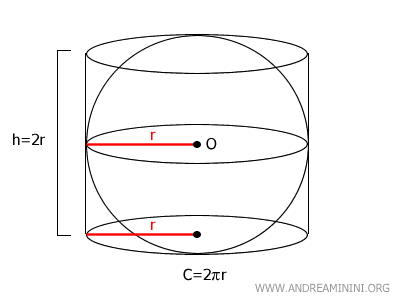
  También puede demostrarse que coincide con el área lateral \( A_L \) del cilindro que la circunscribe perfectamente. $$ A_L = C \cdot h = 2 \pi r \cdot 2r = 4 \pi r^2 $$
  

• Volumen
  El volumen de una esfera es proporcional al cubo de su radio, y se determina con la fórmula: $$ \frac{4}{3}πr^3 $$

Calotas esféricas

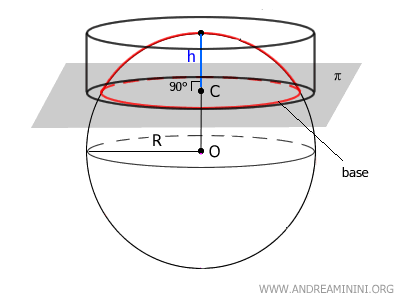
Una calota esférica es una porción de la superficie de una esfera limitada por un plano secante que la corta.

Cuando un plano (π) intersecta una esfera, su superficie queda dividida en dos regiones. Cada una de ellas se denomina calota o casquete esférico.

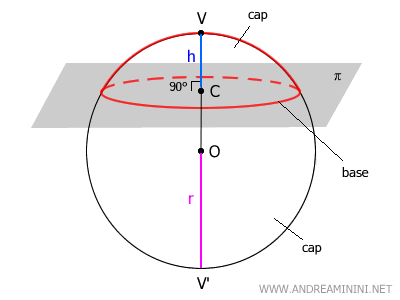
Una calota esférica se caracteriza por tres elementos fundamentales:

• La base: el círculo generado por la intersección del plano con la esfera, centrado en el punto C.
• El vértice (V): el punto más alejado del plano, alineado con el centro de la base sobre el diámetro de la esfera.
• La altura (h): la distancia perpendicular desde el vértice (V) hasta el centro (C) de la base.

El diámetro \( VV' \), que atraviesa el centro de la base, actúa como eje de simetría de la calota, dividiéndola en dos mitades especulares.

Casos particulares

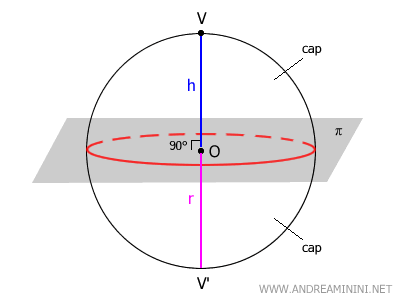
Si el plano (π) pasa por el centro (O) de la esfera, se obtienen dos hemisferios congruentes.

En este caso, cada calota equivale exactamente a la mitad de la superficie de la esfera, y no solamente a un segmento curvo.

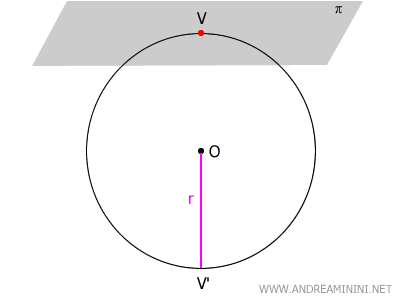
Si el plano (π) es tangente a la esfera, la calota se reduce a un solo punto V sobre su superficie.

Nota. Una calota conserva muchas propiedades geométricas de la esfera, como la curvatura y la simetría, aunque esté definida por una base y un vértice específicos.

Área de una calota esférica

El área de una calota esférica se calcula con la fórmula

$$ A = 2 \pi R h $$

donde \( R \) es el radio de la esfera y \( h \) es la altura de la calota.

Ejemplo

Supongamos una esfera con radio \( R = 5\,cm \). Si se corta exactamente por la mitad, la calota resultante tendrá una altura \( h = R = 5\,cm \).

Aplicando la fórmula, se obtiene:

\[ A = 2 \pi R h = 2 \pi \cdot 5 \cdot 5 = 50 \pi \approx 157.08\,cm^2 \]

Este valor corresponde exactamente a la mitad del área total de la esfera.

Demostración. El área total de la superficie de una esfera está dada por: \[ A_{\text{total}} = 4 \pi R^2 \] Esta fórmula representa el área total de una esfera de radio \( R \). Si se corta por el centro, se obtiene un hemisferio cuya superficie es justo la mitad: \[ A_{\text{hemisferio}} = 2 \pi R^2 \] Consideremos ahora una calota cuya altura \( h \) es igual al radio \( R \). Es decir, cubre un hemisferio completo. Sustituyendo \( h = R \) en la fórmula general del área de una calota, se tiene: \[ S = 2 \pi R h \] que, con \( h = R \), resulta: \[ S = 2 \pi R \cdot R = 2 \pi R^2 \] lo cual coincide exactamente con el área del hemisferio. Esto confirma que la fórmula \( S = 2 \pi R h \) sigue siendo válida incluso en casos límite, como una calota hemisférica.

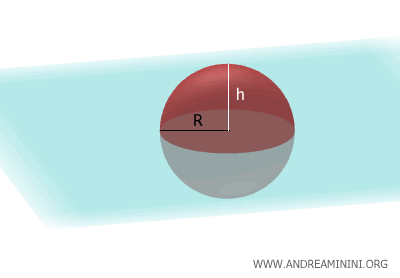
Por tanto, el área de una zona esférica equivale al área lateral de un cilindro con el mismo radio que la esfera y una altura igual a la de la calota. El área lateral del cilindro también se expresa como \( S_L = 2 \pi R h \)

Zona esférica

Una zona esférica es la porción de la superficie de una esfera comprendida entre dos planos paralelos que la atraviesan.

Estos planos cortan la esfera en dos círculos, conocidos como las bases de la zona, y dividen su superficie en tres regiones distintas.

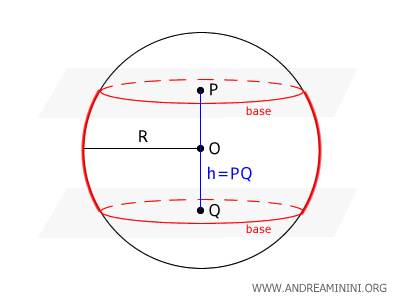
La región intermedia entre los dos planos se denomina zona esférica. Tiene forma de banda curva delimitada por dos cortes circulares.

Nota. Para visualizarla, imagina un globo terráqueo: si trazas dos líneas de latitud, se forma una franja circular entre ellas - eso es una zona esférica.

El diámetro de la esfera que pasa por el segmento \( PQ \), que une los centros \( P \) y \( Q \) de las dos bases, se denomina eje de simetría de la zona. La distancia entre estos dos centros se llama altura de la zona y se indica con \( h \).

Área de una zona esférica

El área superficial \( S \) de una zona esférica se calcula con la misma fórmula que la de una calota esférica:

\[ S = 2 \pi R h \]

donde \( R \) es el radio de la esfera y \( h \) es la distancia entre los dos planos paralelos.

Nota. Una calota esférica es simplemente un caso particular de zona esférica, donde uno de los planos es tangente a la esfera. Por lo tanto, la fórmula es la misma: en ambos casos, el área depende únicamente del radio de la esfera y de la altura de la franja curva.

Ejemplo

Supongamos una esfera de radio \( R = 10\,cm \) cortada por dos planos paralelos que generan una zona de altura \( h = 4\,cm \).

El área de la zona es aproximadamente \( 251.33\,cm^2 \):

$$ S = 2 \pi R h = 2 \pi \cdot 10 \cdot 4 = 80 \pi \approx 251.33\,cm^2 $$

Nota. El área de una zona esférica también puede compararse con el área lateral de un cilindro de igual radio y altura. En efecto, el área lateral de un cilindro se calcula igualmente como \( S_L = 2 \pi R h \).

Cuña esférica

Una cuña esférica es una porción de la superficie de una esfera limitada por dos semiplanos que pasan por su centro.

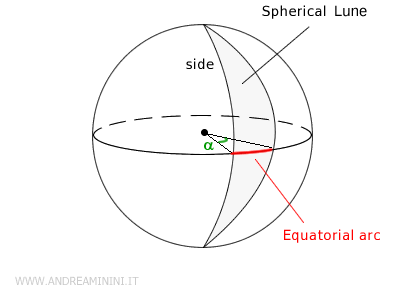
Los elementos principales de una cuña esférica son:

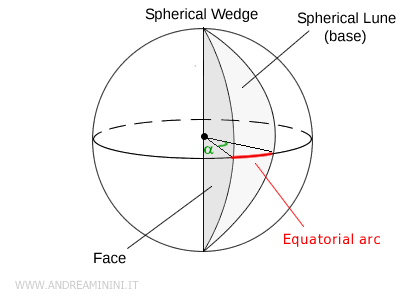
• Ángulo diedro: el ángulo sólido (\( \alpha \)) formado por los dos semiplanos.
• Arco ecuatorial: el tramo del círculo máximo (similar al ecuador terrestre) contenido dentro de la cuña.
• Lados de la cuña: los arcos semicirculares que resultan de la intersección de los semiplanos con la superficie esférica.

De forma sencilla, una cuña esférica se asemeja a una rodaja de naranja, cortada a lo largo de sus segmentos naturales.

Área de una cuña esférica

El área superficial de una cuña esférica depende de la medida de su ángulo diedro y puede calcularse de dos formas:

• Si el ángulo está en radianes: \[ S_f = 2 \alpha_{\text{rad}} R^2 \]
• Si se mide en grados: \[ S_f = \frac{\alpha^\circ}{90^\circ} \pi R^2 \]

En estas expresiones, \( S_f \) es el área de la cuña, \( R \) el radio de la esfera, \( \alpha_{\text{rad}} \) el ángulo en radianes y \( \alpha^\circ \) el mismo ángulo expresado en grados.

Conviene recordar que el área de una cuña es directamente proporcional al valor del ángulo diedro \( \alpha \), en relación con la superficie total de la esfera.

Demostración. El área total de una esfera es: \[ A_{\text{total}} = 4\pi R^2 \] Una cuña representa una fracción de esa superficie, determinada por su ángulo. Si se mide en radianes, la proporción es: \[ A_{\text{cuña}} = 4\pi R^2 \cdot \frac{ \alpha_{\text{rad}} }{2 \pi} = 2\alpha_{\text{rad}} R^2 \] Si se mide en grados, la proporción respecto a los \( 360^\circ \) de un círculo completo es: \[ A_{\text{cuña}} = 4\pi R^2 \cdot \frac{ \alpha^\circ }{360^\circ} = \frac{\alpha^\circ}{90^\circ} \pi R^2 \]

Ejemplo

Calculemos el área de una cuña esférica de una esfera de radio \( R = 5 \, \text{cm} \), con un ángulo diedro de \( 60^\circ \). Usamos la fórmula en grados:

\[ S_f = \frac{60^\circ}{90^\circ} \pi R^2 = \frac{2}{3} \pi \cdot (5)^2 \]

\[ S_f = \frac{2}{3} \pi \cdot 25 = \frac{50}{3} \pi \, \text{cm}^2 \]

Así, el área de la cuña es aproximadamente \( 52.36 \, \text{cm}^2 \).

Ejemplo 2

Ahora consideremos una esfera de radio \( 10 \, \text{cm} \) y una cuña con un ángulo diedro de \( \frac{\pi}{4} \, \text{rad} \). Aplicamos la fórmula para radianes:

\[ S_f = 2 \alpha_{\text{rad}} R^2 = 2 \cdot \frac{\pi}{4} \cdot 10^2 \]

\[ S_f = \frac{\pi}{2} \cdot 100 = 50\pi \, \text{cm}^2 \]

Por tanto, el área de esta cuña es aproximadamente \( 157.08 \, \text{cm}^2 \).

Segmento esférico

Un segmento esférico es una porción de un sólido generada al cortar una esfera mediante uno o dos planos paralelos.

A] Segmento esférico con una base

Un segmento esférico con una base se obtiene al seccionar una esfera con un solo plano y conservar únicamente la parte situada por encima o por debajo de ese plano.

La superficie curva del segmento corresponde a una calota esférica, que recibe el nombre de “media esfera” si el plano divide exactamente la esfera en dos mitades.

La base del segmento es el círculo generado por la intersección entre el plano de corte y la superficie esférica.

Fórmula del volumen

Si el segmento tiene altura \( h \) y la base posee un radio \( r \), su volumen equivale a la suma del volumen de una esfera de diámetro \( h \) y el de un cilindro de igual base y altura \( h/2 \):

$$ V = \frac{4}{3} \pi \left( \frac{h}{2} \right)^3 + \pi r^2 \cdot \frac{h}{2} $$

Es decir, se trata de la combinación del volumen de una semiesfera con el de un cilindro.

Esta fórmula permite calcular tanto el volumen de la porción superior como el de la inferior de un segmento esférico con una sola base.

Versión simplificada de la fórmula

La expresión del volumen puede escribirse también en una forma más compacta:

$$ V = \frac{1}{3} \pi h^2 (3R - h) $$

donde \( R \) representa el radio de la esfera original.

Demostración. Consideremos un segmento esférico con una base, de altura \( h = CV \) y radio de base \( r = BC \).

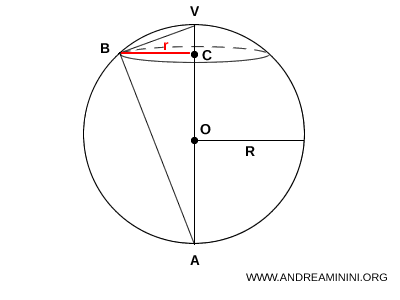
Aplicando el segundo teorema de Euclides al triángulo rectángulo VAB, se obtiene: $$ BC^2 = AC \cdot CV $$ Como \( BC = r \), se tiene: $$ r^2 = AC \cdot h $$ Observando que \( AC = 2R - h \), resulta: $$ r^2 = (2R - h) \cdot h $$ $$ r^2 = 2Rh - h^2 $$ Sustituyendo esta expresión en la fórmula original del volumen: $$ V = \frac{4}{3} \pi \left( \frac{h}{2} \right)^3 + \pi r^2 \cdot \frac{h}{2} $$ $$ V = \frac{4}{3} \pi \cdot \frac{h^3}{8} + \pi (2Rh - h^2) \cdot \frac{h}{2} $$ $$ V = \frac{\pi h^3}{6} + \pi R h^2 - \frac{\pi h^3}{2} $$ $$ \begin{aligned} V &= \pi R h^2 + \left( \frac{1}{6} - \frac{1}{2} \right) \pi h^3 \\ &= \pi R h^2 - \frac{1}{3} \pi h^3 \end{aligned} $$ Factorizando: $$ \boxed{ V = \frac{1}{3} \pi h^2 (3R - h) } $$ que es la forma reducida de la fórmula del volumen de un segmento esférico con una sola base.

B] Segmento esférico con dos bases

Un segmento esférico también puede generarse al cortar una esfera mediante dos planos paralelos, conservando únicamente la parte intermedia.

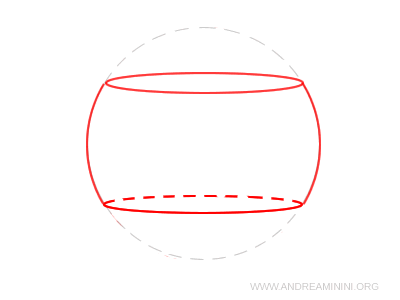
En otras palabras, se trata del sólido comprendido entre dos planos horizontales que seccionan una esfera. La región delimitada por esos cortes constituye el segmento esférico.

La forma resultante recuerda a un cilindro curvado o abombado.

Sus elementos principales son:

• Las bases superior e inferior, que son círculos obtenidos por la intersección de los planos con la esfera.
• La superficie lateral curva, correspondiente a una zona esférica.
• La altura del segmento, \( h \), que es la distancia vertical entre ambos planos.
• El radio \( R \) de la esfera original.

Nota. El segmento esférico no debe confundirse con una calota esférica (que se genera con un solo plano) ni con una cuña esférica (delimitada por dos semiplanos que atraviesan el centro).

Fórmula del volumen

Si el segmento tiene altura \( h \), radios de base \( r_1 \) y \( r_2 \), y la esfera de origen tiene radio \( R \), el volumen se calcula con la siguiente expresión:

$$ V = \frac{\pi h}{6} (3r_1^2 + 3r_2^2 + h^2) $$

Nota. Este volumen puede interpretarse como la suma del volumen de una esfera de diámetro \( h \) y dos cilindros, cada uno con altura \( h/2 \) y bases iguales a las del segmento.

Los volúmenes de los cilindros son: $$ V_1 = \pi r_1^2 \cdot \frac{h}{2} \quad , \quad V_2 = \pi r_2^2 \cdot \frac{h}{2} $$ El volumen de una esfera de radio \( h/2 \) es: $$ V_3 = \frac{4}{3} \pi \left( \frac{h}{2} \right)^3 $$ Sumando los tres: $$ V = V_1 + V_2 + V_3 $$ $$ V = \pi r_1^2 \cdot \frac{h}{2} + \pi r_2^2 \cdot \frac{h}{2} + \frac{4}{3} \pi \cdot \frac{h^3}{8} $$ $$ V = \frac{\pi h}{2} (r_1^2 + r_2^2) + \frac{1}{6} \pi h^3 $$ $$ V = \frac{1}{6} \pi h (3r_1^2 + 3r_2^2 + h^2) $$ que es la fórmula general del volumen para un segmento esférico con dos bases.

Cuña esférica

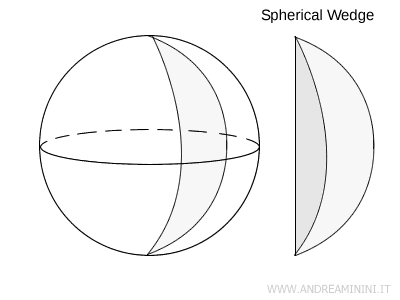
Una cuña esférica es una porción de esfera delimitada por dos planos semicirculares distintos que definen las “caras” del sólido. La superficie curva que las une es una luna esférica, también llamada superficie lateral.

Este sólido se asemeja a un gajo de naranja.

El volumen de una cuña esférica es directamente proporcional al ángulo entre sus dos caras planas.

Si el ángulo se mide en radianes:

$$V : \frac{4}{3} \pi R^3 = \alpha_{rad} : 2\pi$$

De esta proporción se obtiene la fórmula del volumen:

$$V = \alpha_{rad} \cdot \frac{2}{3} R^3$$

Nota. Si el ángulo se expresa en grados, la relación se convierte en: $$V : \frac{4}{3} \pi R^3 = \alpha : 360^\circ$$ De donde se deduce: $$V = \frac{\alpha}{360^\circ} \cdot \frac{4}{3} \pi R^3$$ o, de forma equivalente: $$V = \frac{\alpha}{270^\circ} \pi R^3$$

Anillo esférico

Un anillo esférico es un sólido que resulta de sustraer un tronco de cono inscrito dentro de un segmento esférico con dos bases circulares.

Se construye a partir de un segmento esférico de dos bases, en cuyo interior se inscribe un tronco de cono cuya superficie lateral coincide exactamente con la superficie interna del segmento.

Las dos secciones circulares que delimitan el segmento definen también las bases del tronco de cono.

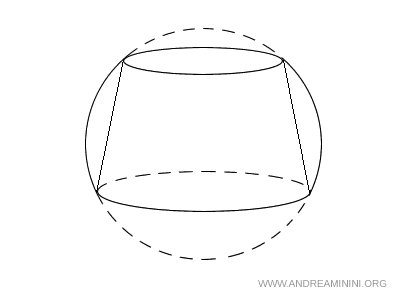
El tronco de cono es la porción de un cono comprendida entre dos planos paralelos a su base. En este caso, sus bases coinciden exactamente con las del segmento esférico.

La región de la esfera comprendida entre la superficie lateral del tronco y la del segmento forma lo que denominamos anillo esférico.

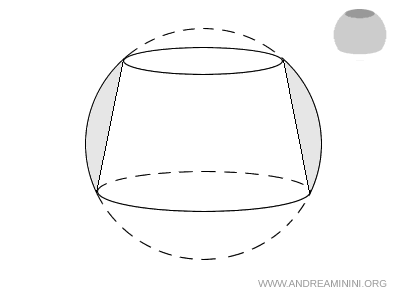
En otras palabras, el anillo esférico es el volumen remanente del segmento esférico tras eliminar el espacio ocupado por el tronco de cono inscrito.

Volumen del anillo esférico

El volumen del anillo esférico se obtiene restando el volumen del tronco de cono al del segmento esférico:

$$ V = \frac{1}{6} \pi a^2 h $$

donde \( a \) es la generatriz (o apotema) del tronco de cono, y \( h \) su altura.

Demostración. Partimos del hecho de que el volumen del anillo esférico es igual a la diferencia entre el volumen del segmento esférico y el del tronco de cono inscrito: $$ V_{\text{anillo}} = V_{\text{segmento esférico}} - V_{\text{tronco de cono}} $$ El volumen del segmento esférico de altura \( h \), con radios de base \( r_1 \) y \( r_2 \), es: $$ V_{\text{segmento esférico}} = \frac{\pi h}{6} \left( 3r_1^2 + 3r_2^2 + h^2 \right) $$ El volumen del tronco de cono con igual altura y radios de base \( r_1 \) y \( r_2 \) es: $$ V_{\text{tronco de cono}} = \frac{1}{3} \pi h \left( r_1^2 + r_1 r_2 + r_2^2 \right) $$ Restando ambos volúmenes: $$ V_{\text{anillo}} = \frac{\pi h}{6} \left( 3r_1^2 + 3r_2^2 + h^2 \right) - \frac{1}{3} \pi h \left( r_1^2 + r_1 r_2 + r_2^2 \right) $$ Llevando a común denominador: $$ V_{\text{anillo}} = \frac{\pi h}{6} \left[ (3r_1^2 + 3r_2^2 + h^2) - 2 (r_1^2 + r_1 r_2 + r_2^2) \right] $$ Desarrollando los términos: $$ V_{\text{anillo}} = \frac{\pi h}{6} \left( r_1^2 + r_2^2 + h^2 - 2 r_1 r_2 \right) $$ Observamos que \( r_1^2 + r_2^2 - 2 r_1 r_2 = (r_1 - r_2)^2 \), por lo que: $$ V_{\text{anillo}} = \frac{\pi h}{6} \left( (r_1 - r_2)^2 + h^2 \right) $$ Dado que geométricamente \( a^2 = (r_1 - r_2)^2 + h^2 \), se concluye que: $$ V_{\text{anillo}} = \frac{1}{6} \pi a^2 h $$ donde \( a \) es la generatriz del tronco de cono y \( h \) la altura del anillo esférico.

Sector esférico

Un sector esférico es una región del espacio delimitada por un cono cuyo vértice coincide con el centro de una esfera y cuya base es una calota esférica.

Dicho de otro modo, es el sólido generado al hacer girar un sector circular 360° alrededor de un eje que no lo atraviesa.

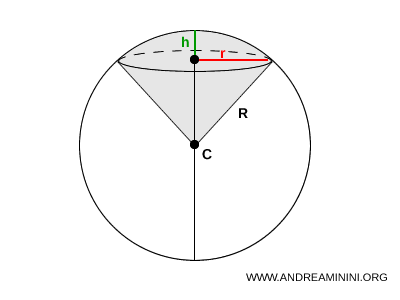
Puede considerarse un cuerpo compuesto por una calota esférica (un segmento esférico de una sola base) y un cono circular recto que comparte dicha base y tiene su vértice en el centro de la esfera.

No obstante, esta interpretación corresponde a un caso particular del sector esférico.

El volumen de un sector esférico viene dado por la fórmula:

$$ V = \frac{2}{3} \pi R^2 h $$

donde \( R \) es el radio de la esfera y \( h \) la altura del segmento esférico (es decir, la distancia entre la base y el centro de la esfera).

El área superficial del sector es:

$$ A = \pi R (2h + r) $$

donde \( r \) es el radio del círculo que constituye la base del sector.

Demostración. Si se descompone el sector esférico en dos sólidos - una calota esférica y un cono cuyo vértice está en el centro de la esfera - es posible deducir la fórmula del volumen a partir de las relaciones geométricas entre sus elementos. El volumen de la calota esférica es: $$ V_{\text{seg}} = \frac{1}{3} \pi h^2 (3R - h) $$ El volumen del cono recto es: $$ V_{\text{cono}} = \frac{1}{3} \pi r^2 (R - h) $$ A partir del triángulo rectángulo formado al seccionar la esfera por el plano de la base, se obtiene la siguiente relación: $$ r^2 = R^2 - (R - h)^2 = 2Rh - h^2 $$ (Para una explicación más detallada, véase la demostración de la fórmula compacta del volumen del segmento esférico). Sumando ambos volúmenes: $$ \begin{aligned} V_{\text{sector}} &= V_{\text{seg}} + V_{\text{cono}} \\ &= \frac{1}{3} \pi \left[ h^2 (3R - h) + r^2 (R - h) \right] \end{aligned} $$ Sustituyendo \( r^2 = 2Rh - h^2 \): $$ \begin{aligned} & h^2 (3R - h) + (2Rh - h^2)(R - h) \\ &= 3Rh^2 - h^3 + 2R^2h - 3Rh^2 + h^3 = 2R^2 h \end{aligned} $$ Por tanto, el volumen del sector esférico se reduce a: $$ \boxed{\, V_{\text{sector}} = \frac{1}{3} \pi (2R^2 h) = \frac{2}{3} \pi R^2 h \,} $$ Es decir, la combinación de los volúmenes del segmento esférico y del cono lleva directamente a la fórmula clásica.

Estas fórmulas se aplican exclusivamente al sector esférico estándar, es decir, aquel delimitado por un cono circular recto cuyo vértice coincide con el centro de la esfera.

En configuraciones más generales - como sectores oblicuos, casquetes huecos o combinaciones con otros sólidos - el cálculo del volumen requiere un análisis geométrico más detallado.

Otras configuraciones de sectores esféricos

Dependiendo de la disposición geométrica, el volumen de un sector esférico puede expresarse como suma o diferencia de otros volúmenes conocidos.

En el ejemplo siguiente, el volumen se calcula restando el volumen combinado de dos conos al de un segmento esférico:

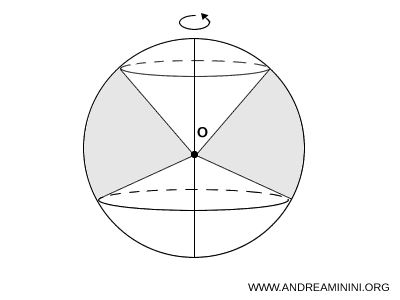
En otro caso, el volumen se obtiene como la diferencia entre los volúmenes de dos sectores esféricos anidados:

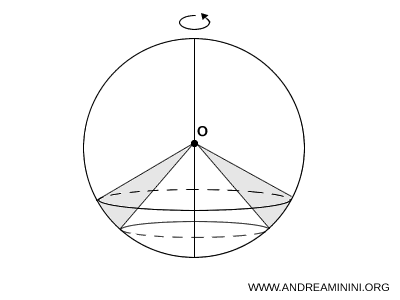
Por ello, es fundamental identificar con precisión la configuración geométrica para aplicar la fórmula adecuada en cada situación.

Esfera en geometría analítica

En geometría analítica, una esfera se define como el conjunto de todos los puntos del espacio que se encuentran a una distancia constante de un punto fijo, llamado centro.

La ecuación canónica de la esfera con centro en el punto \( (x_0, y_0, z_0) \) y radio \( r \) es:

$$ (x - x_0)^2 + (y - y_0)^2 + (z - z_0)^2 = r^2 $$

donde \( (x, y, z) \) representan las coordenadas de un punto cualquiera del espacio tridimensional.

Al desarrollar esta expresión, se obtiene la ecuación general de una superficie esférica:

$$ x^2 + y^2 + z^2 + a x + b y + c z + d = 0 $$

donde \( a = -2x_0 \), \( b = -2y_0 \), \( c = -2z_0 \) y \( d = x_0^2 + y_0^2 + z_0^2 - r^2 \).

Esta forma general puede considerarse como el análogo tridimensional de la ecuación de la circunferencia en el plano cartesiano.

Las coordenadas del centro de la esfera se determinan mediante las siguientes expresiones:

$$ x_0 = - \frac{a}{2}, \qquad y_0 = - \frac{b}{2}, \qquad z_0 = - \frac{c}{2} $$

Es decir, el centro tiene coordenadas:

$$ C = (x_0, y_0, z_0) = \left( - \frac{a}{2}, - \frac{b}{2}, - \frac{c}{2} \right) $$

Cuando la esfera está centrada en el origen O(0, 0, 0), su ecuación se simplifica a:

$$ x^2 + y^2 + z^2 = r^2 $$

El radio de la esfera puede obtenerse a partir de la siguiente fórmula:

$$ r = \sqrt{x_0^2 + y_0^2 + z_0^2 - d} $$

Explicación. Dado que \( d = x_0^2 + y_0^2 + z_0^2 - r^2 \), se puede despejar el radio de la siguiente manera: $$ r^2 = x_0^2 + y_0^2 + z_0^2 - d $$ Tomando la raíz cuadrada: $$ r = \sqrt{x_0^2 + y_0^2 + z_0^2 - d} $$

Si el centro está en el origen, la ecuación de la esfera se reduce nuevamente a:

$$ x^2 + y^2 + z^2 = r^2 $$

A continuación se muestra un ejemplo de una esfera centrada en el origen del sistema cartesiano y con radio unidad.

 

Condición de existencia real de una esfera. Recordando que \( d = x_0^2 + y_0^2 + z_0^2 - r^2 \), se puede reescribir el radio al cuadrado como: $$ r^2 = x_0^2 + y_0^2 + z_0^2 - d $$ Sustituyendo las expresiones de las coordenadas del centro: $$ x_0 = -\frac{a}{2}, \quad y_0 = -\frac{b}{2}, \quad z_0 = -\frac{c}{2} $$ se obtiene: $$ r^2 = \left(-\frac{a}{2}\right)^2 + \left(-\frac{b}{2}\right)^2 + \left(-\frac{c}{2}\right)^2 - d $$ lo que equivale a: $$ r^2 = \frac{a^2}{4} + \frac{b^2}{4} + \frac{c^2}{4} - d $$ Para que esta cantidad sea mayor o igual a cero (es decir, para que el radio sea real), debe cumplirse la siguiente condición: $$ \frac{a^2}{4} + \frac{b^2}{4} + \frac{c^2}{4} - d \ge 0 $$

Ejemplo

Consideremos una esfera con centro en el punto \( C: (1, 2, -1) \) y radio \( r = 3 \).

La ecuación canónica es:

$$ (x - x_0)^2 + (y - y_0)^2 + (z - z_0)^2 = r^2 $$

Sustituyendo los valores: \( x_0 = 1, \quad y_0 = 2, \quad z_0 = -1 \)

$$ (x - 1)^2 + (y - 2)^2 + (z + 1)^2 = 3^2 $$

Desarrollando los binomios: $$ (x^2 - 2x + 1) + (y^2 - 4y + 4) + (z^2 + 2z + 1) = 9 $$

Reduciendo términos: $$ x^2 + y^2 + z^2 - 2x - 4y + 2z + 1 + 4 + 1 - 9 = 0 $$

Finalmente: $$ x^2 + y^2 + z^2 - 2x - 4y + 2z - 3 = 0 $$

Hemos obtenido así la ecuación general de la superficie esférica.

Verificación de la condición de realidad. En este caso, los coeficientes son: \( a = -2 \), \( b = -4 \), \( c = 2 \), \( d = -3 \) Verificamos la condición: $$ \frac{a^2}{4} + \frac{b^2}{4} + \frac{c^2}{4} - d \ge 0 $$ Sustituyendo: $$ \frac{(-2)^2}{4} + \frac{(-4)^2}{4} + \frac{2^2}{4} - (-3) \ge 0 $$ $$ \frac{4}{4} + \frac{16}{4} + \frac{4}{4} + 3 \ge 0 $$ $$ 1 + 4 + 1 + 3 = 9 \ge 0 $$ La condición se cumple, por tanto la ecuación \( x^2 + y^2 + z^2 - 2x - 4y + 2z - 3 = 0 \) representa efectivamente una superficie esférica real.

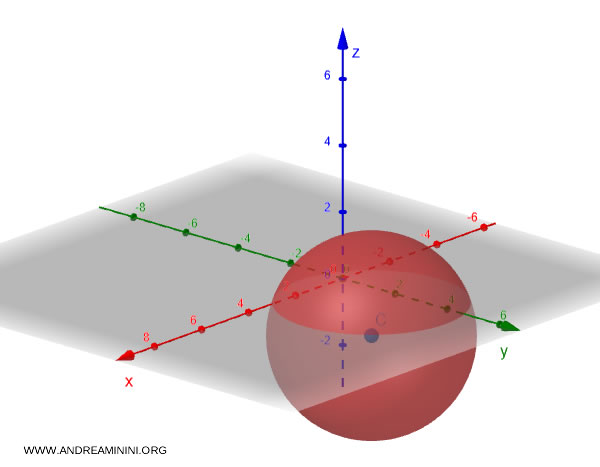
Demostración

Una superficie esférica está formada por todos los puntos del espacio que se encuentran a una distancia igual al radio \( r \) respecto del centro \( (x_0, y_0, z_0) \) de la esfera.

$$ \sqrt{(x - x_0)^2 + (y - y_0)^2 + (z - z_0)^2} = r $$

Elevando ambos miembros al cuadrado, se obtiene:

$$ \left(\sqrt{(x - x_0)^2 + (y - y_0)^2 + (z - z_0)^2}\right)^2 = r^2 $$

$$ (x - x_0)^2 + (y - y_0)^2 + (z - z_0)^2 = r^2 $$

Desarrollando cada término:

$$ x^2 - 2x x_0 + x_0^2 + y^2 - 2y y_0 + y_0^2 + z^2 - 2z z_0 + z_0^2 = r^2 $$

Definiendo los coeficientes como \( a = -2x_0 \), \( b = -2y_0 \), y \( c = -2z_0 \), la ecuación toma la forma:

$$ x^2 + a x + x_0^2 + y^2 + b y + y_0^2 + z^2 + c z + z_0^2 = r^2 $$

Reuniendo todos los términos en el mismo miembro:

$$ x^2 + y^2 + z^2 + a x + b y + c z + (x_0^2 + y_0^2 + z_0^2 - r^2) = 0 $$

Finalmente, agrupando las constantes en un solo término \( d \), con \( d = x_0^2 + y_0^2 + z_0^2 - r^2 \), se obtiene:

$$ x^2 + y^2 + z^2 + a x + b y + c z + d = 0 $$

Esta es la forma general de la ecuación de una superficie esférica.

Ecuación de la esfera en coordenadas esféricas

La ecuación de una esfera también puede expresarse utilizando coordenadas esféricas, lo que resulta especialmente útil en contextos de simetría radial:

$$ \begin{cases} x = x_0 + r \sin \theta \cos \phi \\ \\ y = y_0 + r \sin \theta \sin \phi \\ \\ z = z_0 + r \cos \theta \end{cases} $$

Donde:

• \( r \) es la distancia radial desde el centro de la esfera;
• \( \theta \) es el ángulo polar (medido desde el eje \( z \));
• \( \phi \) es el ángulo azimutal (medido en el plano \( xy \) desde el eje \( x \)).

Notas adicionales

A continuación se presentan algunas consideraciones complementarias sobre las esferas:

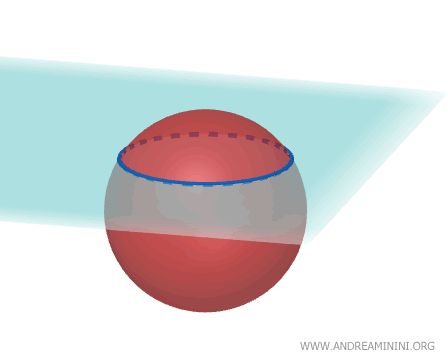
• Secciones planas
  La intersección de un plano con una esfera siempre da lugar a un círculo. Si el plano pasa por el centro, el círculo obtenido es el mayor posible (el círculo máximo).
  
• Cuerda
  Una cuerda es un segmento que une dos puntos distintos sobre la superficie esférica. Todas las cuerdas están contenidas en planos secantes a la esfera.
• Diámetro
  El diámetro de una esfera es una cuerda que pasa por su centro y mide el doble del radio: $$ d = 2r $$
• Relación entre un plano y una esfera
  Sea \( \alpha \) un plano y \( \Sigma \) una esfera de centro \( C \) y radio \( r \). Existen tres posibilidades según la distancia entre el plano y el centro de la esfera:
  • Plano externo: si la distancia es mayor que el radio (\( d > r \)), el plano no intersecta la esfera.
  • Plano tangente: si la distancia es exactamente igual al radio (\( d = r \)), el plano toca la esfera en un único punto.
  • Plano secante: si la distancia es menor que el radio (\( d < r \)), el plano corta la esfera y la intersección es un círculo.
• Hiperesfera (o n-esfera)
  Es la generalización de la esfera a dimensiones superiores. Por ejemplo, una 4-esfera es el análogo en cuatro dimensiones de la esfera tridimensional.
• Teorema de los segmentos tangentes trazados desde un punto exterior
  Todos los segmentos tangentes trazados desde un punto exterior \( P \) a una esfera son congruentes: $$ \overline{AP} \cong \overline{BP} \cong \overline{CP} \cong \overline{DP} $$ Estos segmentos generan un cono circular cuya base está sobre la esfera y cuyo vértice es el punto \( P \).
  

Estos son solo algunos aspectos adicionales que enriquecen el estudio geométrico de la esfera.