Tronco de cono

Un tronco de cono es un sólido geométrico que se obtiene al cortar un cono mediante un plano paralelo a su base.

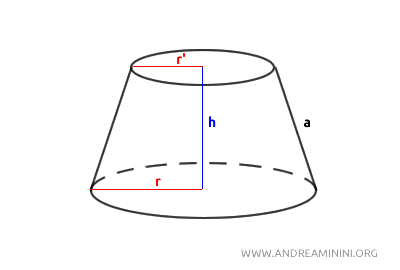
Este procedimiento genera una figura con dos bases circulares de distinto radio: la base mayor (la original del cono) y una base menor que corresponde a la sección realizada por el plano.

Las caras laterales del tronco son inclinadas, y si se prolongaran sus generatrices, estas convergerían en un punto situado por encima de la base mayor.

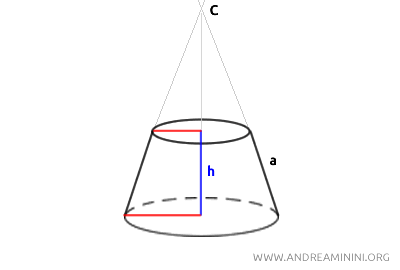
En otras palabras, las líneas imaginarias que resultan de extender la generatriz inclinada (a) del cono se encuentran en el punto C, que representa la proyección del vértice original del cono.

Propiedades del tronco de cono

Un tronco de cono puede generarse haciendo girar un trapecio 360° en torno al lado perpendicular a sus bases paralelas, el cual corresponde a la altura (h) del sólido.

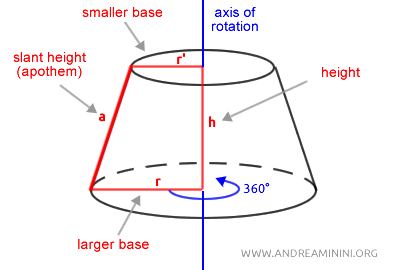
La recta en torno a la cual gira el trapecio se denomina eje de rotación.

El lado inclinado del trapecio se convierte en la generatriz (a) del tronco de cono, es decir, la altura de su superficie lateral.

Nota: Esta forma geométrica es muy habitual tanto en el ámbito matemático como en la vida cotidiana: vasos de papel, pantallas de lámpara o componentes arquitectónicos como cúpulas, torres y chimeneas. También se emplea en el diseño de altavoces, ya que mejora la direccionalidad del sonido y la eficiencia en su propagación.

Fórmulas

Las dimensiones fundamentales de un tronco de cono son su altura (distancia vertical entre las dos bases), el radio de la base mayor y el radio de la base menor.

• Área de las bases
  Las áreas de las dos bases deben calcularse por separado, ya que sus radios son diferentes (r ≠ r').
  
  • Base mayor $$ A_B = \pi r^2 $$
  • Base menor $$ A'_B = \pi r'^2 $$

  Nota. La suma de las áreas de las bases del tronco de cono es: $$ A_B + A'_B = \pi r^2 + \pi r'^2 = \pi ( r^2 + r'^2 ) $$

• Área lateral
  La superficie lateral A_L se calcula utilizando la generatriz (a) del tronco: $$ A_L = \pi a (r + r') $$

  Nota. El área lateral equivale al producto de la generatriz por la suma de las semicircunferencias de ambas bases. $$ A_L = a \cdot ( \frac{1}{2} \cdot 2 \pi r + \frac{1}{2} \cdot 2 \pi r') $$ $$ A_L = a \cdot (\ \pi r +\ \pi r') $$ $$ A_L = a \cdot \pi \cdot (r +\ r') $$

• Área total
  El área total se obtiene sumando el área lateral y las áreas de las dos bases: $$ A_T = A_L + A_B + A'_B $$
• Volumen
  El volumen del tronco de cono se determina mediante la fórmula: $$ V = \frac{1}{3} \pi h (r^2 + r'^2 + r \cdot r') $$ donde h es la altura del tronco, r es el radio de la base mayor y r' el de la base menor.
  Demostración. Consideremos un cono grande de radio $ R $ y altura $ H $, al que se le ha recortado un cono más pequeño de radio $ r' $ y altura $ h' $.
  
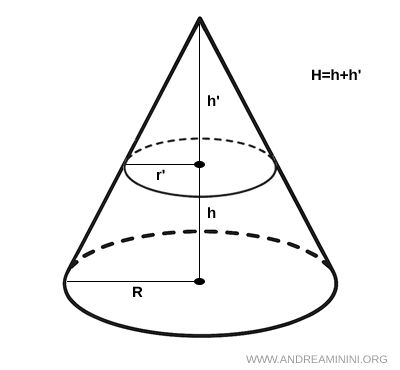
  Como ambos conos son semejantes, se cumple la proporción: $$ r':R = h':H $$ y como $ H = h + h' $, entonces: $$ r':R = h':(h + h') $$ Expresado como fracción: $$ \frac{r'}{R} = \frac{h'}{H} = \frac{h'}{h + h'} $$ Despejando $ h' $ obtenemos: $$ \frac{r'}{R} = \frac{h'}{h + h'} $$ $$ r'(h + h') = R h' $$ $$ r'h + r'h' = R h' $$ $$ r'h = h'(R - r') $$ $$ h' = \frac{r'}{R - r'} \cdot h $$ Ahora calculemos los volúmenes de los dos conos:

  • $V_1 = \frac{1}{3} \pi R^2 (h + h')$ (volumen del cono original)
  • $V_2 = \frac{1}{3} \pi r'^2 h'$ (volumen del cono que se ha retirado)

  El volumen del tronco es la diferencia entre ambos: $$ V = V_1 - V_2 $$ $$ V = \frac{1}{3} \pi \left[ R^2(h + h') - r'^2 h' \right] $$ $$ V = \frac{1}{3} \pi \left[ R^2 h + (R^2 - r'^2) h' \right] $$ Sustituyendo $ h' = \frac{r'}{R - r'} \cdot h $ resulta: $$ V = \frac{1}{3} \pi \left[ R^2 h + (R^2 - r'^2) \cdot \frac{r'}{R - r'} \cdot h \right] $$ $$ V = \frac{1}{3} \pi h \left[ R^2 + \frac{r'(R^2 - r'^2)}{R - r'} \right] $$ Utilizando la identidad $ R^2 - r'^2 = (R - r')(R + r') $, obtenemos: $$ V = \frac{1}{3} \pi h \left[ R^2 + \frac{r'(R - r')(R + r')}{R - r'} \right] $$ $$ V = \frac{1}{3} \pi h \left[ R^2 + r'(R + r') \right] $$ $$ V = \frac{1}{3} \pi h (R^2 + Rr' + r'^2) $$ Por lo tanto, llegamos a la fórmula definitiva: $$ V = \frac{1}{3} \pi h (R^2 + r'^2 + Rr') $$

Relación entre las áreas de los círculos en un cono y sus distancias al vértice

Cuando un cono se corta con un plano paralelo a su base, la intersección es un círculo más pequeño, similar al de la base en sentido geométrico.

En figuras semejantes, las dimensiones lineales correspondientes guardan una proporción constante; en cambio, las áreas se relacionan según el cuadrado de esa proporción y los volúmenes, según el cubo.

De ahí que las áreas del círculo de la base y del círculo seccionado estén vinculadas por una relación matemática precisa, en función de sus distancias al vértice del cono.

Ejemplo práctico

Consideremos un tronco de cono cuya altura original es \( h_1 = 12 \, \text{cm} \),

y en el que la sección paralela se realiza a \( h_2 = 4 \, \text{cm} \) del vértice.

La razón entre las dos áreas será:

\[ \frac{A_1}{A_2} = \left( \frac{12}{4} \right)^2 = 3^2 = 9 \]

Por tanto, podemos concluir que:

\[ A_1 = 9 \cdot A_2 \]

En otras palabras: el área de la base es nueve veces mayor que la del círculo superior.

Demostración

Supongamos un cono y una sección realizada por un plano paralelo a su base.

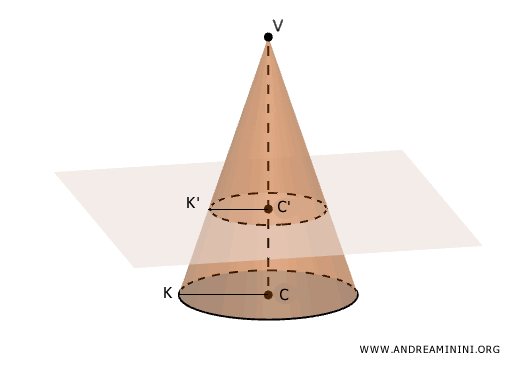
Los triángulos VCK y VC'K' son semejantes de acuerdo con el primer criterio de semejanza de triángulos, ya que tienen sus ángulos correspondientes iguales.

Esto implica que los lados correspondientes son proporcionales:

$$ VC : VC' = CK : C'K' $$

Que puede expresarse como:

$$ \frac{VC}{VC'} = \frac{CK}{C'K'} $$

Elevando ambos términos al cuadrado:

$$ \left( \frac{VC}{VC'} \right)^2 = \left( \frac{CK}{C'K'} \right)^2 $$

$$ \frac{VC^2}{VC'^2} = \frac{CK^2}{C'K'^2} $$

Recordando que el área de un círculo es \( A = \pi r^2 \), se deduce que la razón entre las áreas es igual al cuadrado de la razón entre sus radios:

$$ \frac{ \pi \cdot (CK)^2}{ \pi \cdot (C'K')^2} = \frac{ CK^2 }{ C'K'^2 } $$

Donde \( A = \pi \cdot (CK)^2 \) representa el área de la base, y \( A_s = \pi \cdot (C'K')^2 \) el área de la sección circular.

En consecuencia:

$$ \frac{ A}{ A_s} = \frac{ CK^2 }{ C'K'^2 } $$

Y por transitividad, la relación entre las áreas coincide con la relación entre los cuadrados de sus distancias al vértice:

$$ \frac{VC^2}{VC'^2} = \frac{CK^2}{C'K'^2} = \frac{ A}{ A_s} $$

$$ \frac{VC^2}{VC'^2} =  \frac{ A}{ A_s} $$

Lo cual completa la demostración.

Y así sucesivamente.