Poliedros
Un poliedro es un sólido tridimensional limitado por caras planas, aristas y vértices.
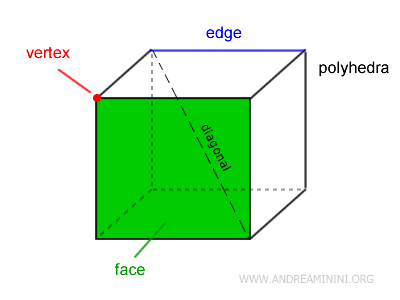
Las caras de un poliedro son polígonos (como triángulos, cuadrados, pentágonos, etc.) situados en distintos planos, sin que se corten entre sí dentro del sólido. Un poliedro posee al menos cuatro caras, siendo el más sencillo el tetraedro. Un pentaedro tiene cinco caras, un hexaedro seis, un octaedro ocho, y así sucesivamente.
Las aristas son los segmentos de recta donde se encuentran dos caras de un poliedro. Constituyen los lados de los polígonos que conforman cada cara.
Cada arista está asociada a un ángulo diedro, que es el ángulo formado por los dos planos de las caras que se intersectan a lo largo de dicha arista.

Los vértices son los puntos donde concurren tres o más aristas. Representan las esquinas de las caras del poliedro.
Cada vértice está asociado a un ángulo sólido, definido por las aristas y las caras que convergen en ese punto.
Los poliedros han cautivado a matemáticos, artistas y filósofos durante milenios. Platón, por ejemplo, mostró un gran interés por los poliedros regulares, hoy conocidos como “sólidos platónicos”. Más allá de las matemáticas, los poliedros tienen numerosas aplicaciones en ciencia e ingeniería. Por ejemplo, muchas estructuras moleculares en química presentan formas poliedricas. También se emplean ampliamente en arquitectura y en las artes.
En un poliedro, una diagonal es un segmento de recta que une dos vértices que no pertenecen a la misma cara.
La superficie de un poliedro es la suma de las áreas de todas sus caras.
Poliedros Regulares e Irregulares
Los poliedros se clasifican en regulares o irregulares.
- Poliedros Regulares (o Sólidos Platónicos)
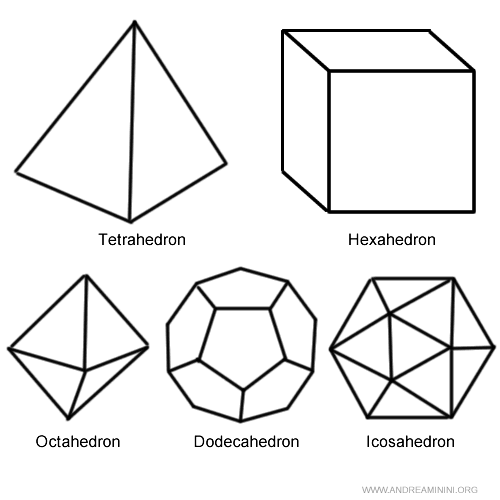
Los poliedros regulares presentan todas sus caras congruentes y ángulos iguales. Sus caras son polígonos regulares, idénticos entre sí. Tanto los ángulos interiores como los ángulos diedros son congruentes. A estos poliedros se los conoce también como sólidos platónicos.Nota: En el plano, los polígonos regulares pueden tener cualquier número de lados. Sin embargo, en el espacio tridimensional solo existen cinco poliedros regulares: el tetraedro, el hexaedro, el octaedro, el dodecaedro y el icosaedro.
- Poliedros Irregulares
Los poliedros irregulares no tienen todas sus caras ni ángulos iguales. Por ejemplo, un prisma es un caso típico de poliedro irregular, ya que puede presentar bases de distintas formas poligonales.
Fórmula de Euler
La fórmula de Euler expresa la relación entre el número de vértices (V), aristas (E) y caras (F) de un poliedro simple y conexo (sin perforaciones ni huecos).
Para un poliedro simple y conexo, el número de vértices (V) menos el número de aristas (E) más el número de caras (F) es siempre igual a 2. $$ V - E + F = 2 $$
Por ejemplo, un cubo posee 6 caras cuadradas, 8 vértices y 12 aristas.
$$ F = 6 $$
$$ V = 8 $$
$$ E = 12 $$
Sustituyendo estos valores en la fórmula de Euler:
$$ V - E + F = 2 $$
$$ 8 - 12 + 6 = 2 $$
$$ 2 = 2 $$
La igualdad se cumple.
¿Para qué sirve? La fórmula de Euler permite verificar si una combinación de vértices, aristas y caras puede corresponder a un poliedro simple y conexo. Si no se cumple la igualdad, esa combinación no puede representar un poliedro de ese tipo. Esta fórmula, por ejemplo, ha sido clave para demostrar que solo existen cinco poliedros regulares, conocidos como sólidos platónicos.
Sólidos Platónicos
Los sólidos platónicos son los cinco poliedros regulares conocidos.
- Tetraedro
Este poliedro cuenta con 4 caras triangulares, 4 vértices y 6 aristas. Cada cara es un triángulo equilátero. - Hexaedro
Este poliedro regular es más conocido como “cubo”. Tiene 6 caras cuadradas, 8 vértices y 12 aristas. Cada cara es un cuadrado. - Octaedro
Presenta 8 caras triangulares, 6 vértices y 12 aristas. - Dodecaedro
Este poliedro posee 12 caras pentagonales, 20 vértices y 30 aristas. Cada cara es un pentágono. - Icosaedro
Cuenta con 20 caras triangulares, 12 vértices y 30 aristas.
Demostración
Se puede demostrar de manera rigurosa que únicamente existen cinco poliedros regulares. Este resultado se fundamenta en que, en cada vértice de un poliedro, la suma de los ángulos interiores de las caras que convergen en él debe ser estrictamente inferior a un ángulo completo (360°).
Comencemos analizando un poliedro regular cuyas caras sean triángulos equiláteros congruentes.
Cada ángulo de un triángulo equilátero mide 60°. Por tanto, no pueden confluir más de 5 de estas caras en un mismo vértice, ya que la suma total debe mantenerse por debajo de 360°. Por ejemplo, \(6 \times 60° = 360°\), lo cual resulta excesivo para que pueda formarse una figura tridimensional en ese punto.
| Polígono regular | Número de caras en un vértice | Suma de ángulos en el vértice | Poliedro |
|---|---|---|---|
| triángulos equiláteros (ángulos de 60°) |
3 | 180° < 360° | tetraedro |
| 4 | 240° < 360° | octaedro | |
| 5 | 300° < 360° | icosaedro | |
| 6 | 360° = 360° | no existe |
Estudiemos ahora un poliedro regular cuyas caras sean cuadrados.
Dado que cada ángulo interior de un cuadrado mide 90°, solo pueden coincidir tres cuadrados en un mismo vértice sin superar el límite. Si se reunieran cuatro, la suma sería exactamente 360°, lo cual impide la formación de un sólido tridimensional: \(4 \times 90^\circ = 360^\circ\).
| Polígono regular | Número de caras en un vértice | Suma de ángulos en el vértice | Poliedro |
|---|---|---|---|
| cuadrados (ángulos de 90°) |
3 | 270° < 360° | cubo |
| 4 | 360° = 360° | no existe |
Pasemos ahora al caso de un poliedro regular cuyas caras sean pentágonos regulares.
Cada ángulo interior de un pentágono regular mide 108°. Así, como máximo pueden converger tres pentágonos en un vértice; si se reunieran cuatro, la suma sería \(4 \times 108^\circ = 432^\circ\), lo que excede claramente el límite de 360° y, por tanto, resulta imposible.
| Polígono regular | Número de caras en un vértice | Suma de ángulos en el vértice | Poliedro |
|---|---|---|---|
| pentágonos (ángulos de 108°) |
3 | 324° < 360° | dodecaedro |
| 4 | 432° > 360° | no existe |
Analicemos ahora el caso de un poliedro regular formado por hexágonos regulares.
Cada ángulo interior de un hexágono regular mide 120°. Incluso si solo se unieran tres caras en un vértice, la suma sería \(3 \times 120^\circ = 360^\circ\), alcanzando exactamente el límite superior, lo que impide la formación de un ángulo sólido y, por ende, de un poliedro tridimensional.
| Polígono regular | Número de caras en un vértice | Suma de ángulos en el vértice | Poliedro |
|---|---|---|---|
| hexágonos (ángulos de 120°) |
3 | 360° = 360° | no existe |
A partir de este punto, no resulta necesario considerar polígonos regulares con más de seis lados, pues la suma de sus ángulos en un vértice solo aumentaría, imposibilitando así la existencia de un sólido tridimensional.
Queda así demostrado que solo existen cinco poliedros regulares: el tetraedro, el cubo, el octaedro, el dodecaedro y el icosaedro.
Ángulos Diedros de un Poliedro
Cada arista de un poliedro está asociada a un ángulo diedro, formado por los dos planos de las caras que se encuentran a lo largo de dicha arista.
Por ejemplo, cada arista de un cubo es la intersección de dos cuadrados que se hallan en planos distintos.
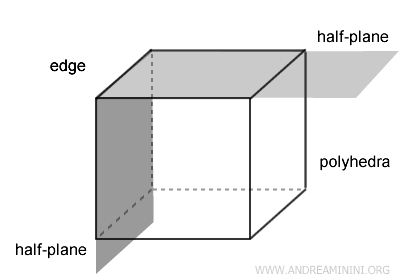
El ángulo diedro asociado a la arista constituye, por tanto, un ángulo diedro del polígono.
Desarrollo Plano de un Poliedro
La superficie total de un poliedro es igual a la suma de las áreas de todas sus caras.
Para estudiar la superficie de un poliedro, se emplea con frecuencia su desarrollo plano, que es una representación bidimensional del sólido.
El desarrollo plano de un poliedro es una representación en dos dimensiones obtenida al “desplegar” sus caras sobre un plano.
Gracias al desarrollo plano, es posible visualizar todas las caras del poliedro en un solo plano, sin solapamientos, manteniendo las proporciones y las conexiones entre las distintas superficies.
Esto facilita enormemente el estudio de las superficies laterales y de las bases del poliedro.
Ejemplo
El desarrollo de un cubo adopta la forma de una cruz formada por 6 cuadrados, cada uno correspondiente a una de sus caras.
Cada lado de los cuadrados en el plano se corresponde con una arista del cubo.
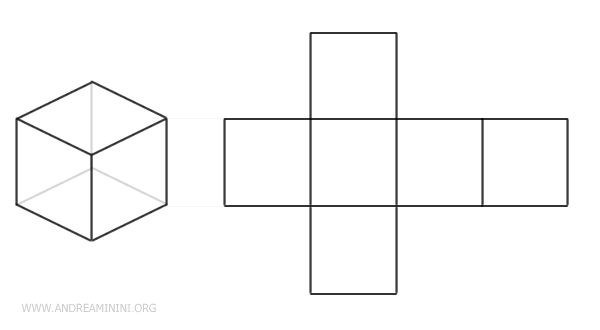
Este es solo uno de los múltiples modos posibles de desplegar un cubo.
En los desarrollos planos de paralelepípedos, se emplean superficies rectangulares en lugar de cuadradas.
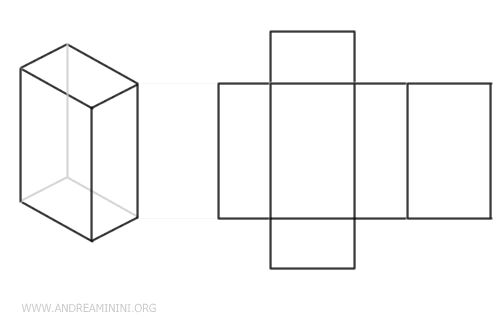
Las superficies centrales corresponden a las caras laterales del paralelepípedo, mientras que las superiores e inferiores constituyen sus bases.
Y así sucesivamente.