Cilindro
Un cilindro es un sólido generado al hacer girar completamente un rectángulo alrededor de una recta (denominada "eje") que pasa por uno de sus lados.
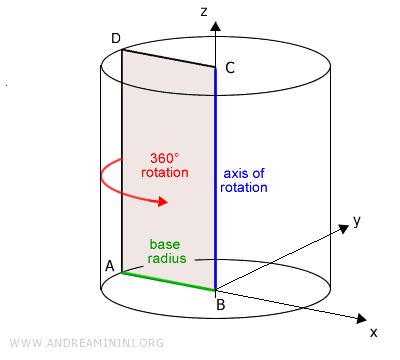
Por tanto, el cilindro es un tipo de sólido de revolución.
La distancia entre el eje de rotación y el lado opuesto del rectángulo se conoce como "radio de la base" o "radio del cilindro".
El cilindro está delimitado por dos superficies circulares llamadas "bases" y una superficie lateral curva que las conecta.
La altura del cilindro es la distancia entre las dos bases. Corresponde al lado del rectángulo que actúa como eje de rotación y es perpendicular a las bases.
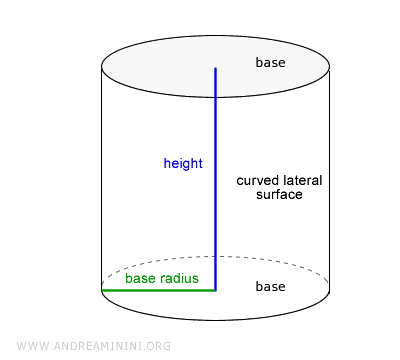
Cuando la altura del cilindro es igual al diámetro de su base, se denomina cilindro equilátero.
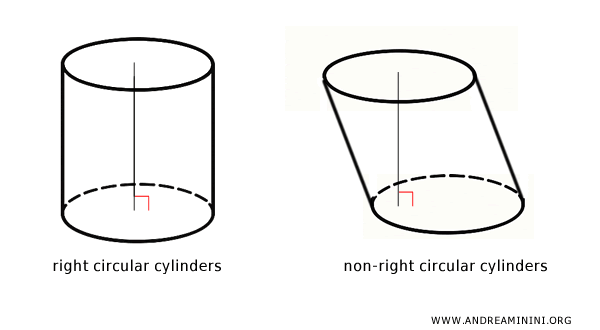
Nota: En geometría elemental, el término "cilindro" suele hacer referencia a un cilindro circular recto. No obstante, existen otros tipos de cilindros, denominados cilindros indefinidos, como el cilindro elíptico, el parabólico, el hiperbólico y diversas variantes de cilindros circulares oblicuos. A diferencia del cilindro circular recto, estos no pueden obtenerse simplemente mediante la rotación de un rectángulo. En estos casos, la altura del cilindro no coincide con el eje de rotación.
Fórmulas
A continuación, se presentan las fórmulas fundamentales para un cilindro circular recto:
- Área de la base
Se calcula como el área de un círculo: $$ S_B = \pi r^2 $$ - Área lateral
Corresponde al producto entre la circunferencia de la base y la altura del cilindro:
$$ S_L = 2 \pi r \cdot h $$ donde \( r \) es el radio de la base y \( \pi \) es la constante pi (aproximadamente 3,14159). - Área total
Es la suma del área lateral y la de las dos bases. Como las bases son círculos, su área es \( \pi r^2 \) cada una. La fórmula queda así:
$$ S_T = S_L + 2 \pi r^2 $$ $$ S_T = 2 \pi r h + 2 \pi r^2 $$ $$ S_T = 2 \pi r (h + r) $$Explicación. Para visualizar esta fórmula, imaginemos que "desenrollamos" la superficie del cilindro sobre un plano.
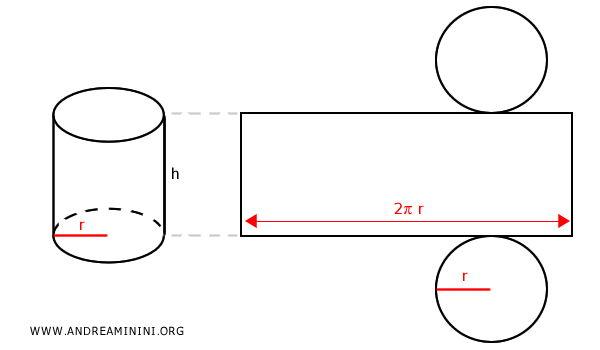
Al desplegar el cilindro, su superficie lateral adopta la forma de un rectángulo, cuya base equivale a la circunferencia de la base (2πr), y cuya altura coincide con la del cilindro (h).
$$ S_L = 2 \pi r h $$
El área de cada base es la de un círculo:
$$ S_B = \pi r^2 $$
Por tanto, el área total se obtiene sumando el área lateral y la de las dos bases:
$$ S_T = 2 S_B + S_L $$ $$ S_T = 2 \pi r^2 + 2 \pi r h $$ $$ S_T = 2 \pi r (r + h) $$ - Volumen
El volumen \( V \) de un cilindro circular recto se obtiene multiplicando el área de la base por la altura \( h \):
$$ V = \pi r^2 h $$
Esta fórmula es válida incluso en el caso de cilindros oblicuos, ya que el volumen depende únicamente del área de la base y de la altura perpendicular.
Nota. Según el teorema de equivalencia de volúmenes para cilindros y prismas, el volumen se expresa como:
$$ V = A \cdot h = \pi r^2 h $$
Tipos de cilindros
Los cilindros pueden clasificarse en distintas categorías:
- Cilindro circular recto
Tiene bases circulares y una superficie lateral perpendicular a ellas. - Cilindro circular oblicuo
También tiene bases circulares, pero su superficie lateral no es perpendicular a las bases; puede estar inclinada o presentar torsiones. - Cilindro oblicuo
Cuando las generatrices están inclinadas respecto a las bases, el cilindro es oblicuo. En este caso, la sección transversal no es un rectángulo. - Cilindro elíptico
Posee bases elípticas en lugar de circulares. - Cilindro parabólico
Se extiende indefinidamente en una dirección y su sección transversal es una parábola. - Cilindro hiperbólico
Similar al parabólico, pero con sección transversal en forma de hipérbola.
Estos son solo algunos ejemplos de cilindros indefinidos o no rectos. Existen muchas otras variantes, dependiendo de la forma de las bases y de cómo se desarrolla la superficie lateral.
El cilindro en la geometría analítica
En geometría analítica, un cilindro puede representarse mediante ecuaciones en coordenadas cartesianas, cilíndricas o esféricas.
Un cilindro circular recto, cuyo eje coincide con el eje \( z \) y con el centro de la base en el origen, se describe con la ecuación:
$$ x^2 + y^2 = r^2 $$
donde \( r \) es el radio de las bases circulares.
Esta ecuación define todos los puntos \( (x, y, z) \) cuya distancia al eje \( z \) es constante e igual a \( r \).

Dado que esta superficie se prolonga infinitamente, para representar un cilindro finito se debe acotar el intervalo de valores en el eje \( z \).
Por ejemplo, si el cilindro va desde el origen \( (0,0,0) \) hasta una altura \( h \), el intervalo correspondiente es:
$$ 0 \le z \le h $$
El resultado es un cilindro de altura finita con su base apoyada sobre el plano \( xy \).
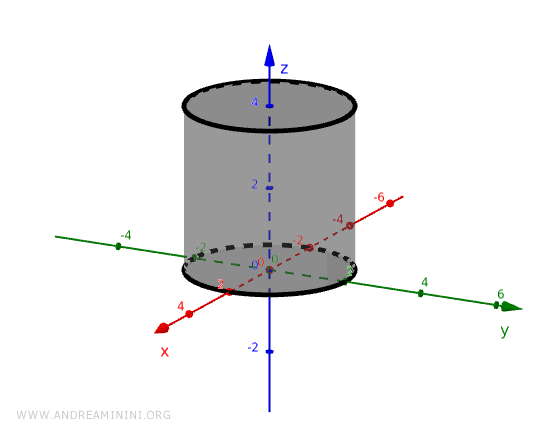
Cilindro circular
La ecuación general de un cilindro circular infinito es: $$ x^2 + y^2 + a x + b y + c = 0 $$
Esta ecuación define una superficie cilíndrica circular si, y solo si, la curva directriz en el plano $xy$ es una circunferencia. Esto ocurre precisamente cuando se cumple la siguiente condición:
$$ \frac{a^2}{4} + \frac{b^2}{4} - c \ge 0 $$
El calificativo “infinito” indica que el cilindro no tiene una altura limitada: se extiende indefinidamente a lo largo de su eje generador en ambas direcciones.
Demostración. Consideramos la ecuación: $$ x^2 + a x + y^2 + b y + c = 0 $$ Agrupamos términos semejantes: $$ (x^2 + a x) + (y^2 + b y) + c = 0 $$ Completamos cuadrados sumando y restando \( \frac{a^2}{4} \) y \( \frac{b^2}{4} \):
$$ (x + \frac{a}{2})^2 + (y + \frac{b}{2})^2 = \frac{a^2}{4} + \frac{b^2}{4} - c $$
Para que la ecuación represente una circunferencia real (es decir, con radio real y definido), el segundo miembro debe ser no negativo:
$$ \frac{a^2}{4} + \frac{b^2}{4} - c \ge 0 $$
Este razonamiento puede extenderse a otros planos coordenados:
- En el plano xz, la ecuación en $x$ y $z$ es: $$ x^2 + z^2 + a x + b z + c = 0 $$ En este caso, el cilindro es circular y su eje es paralelo al eje $y$.
- En el plano yz, la ecuación en $y$ y $z$ es: $$ y^2 + z^2 + a y + b z + c = 0 $$ Aquí, el cilindro es circular y su eje es paralelo al eje $x$.
Ejemplo
Consideremos el cilindro definido por la ecuación:
$$ \frac{x^2}{4} + \frac{y^2}{4} = 1 $$
Esta es la expresión estándar de un cilindro circular infinito, con eje paralelo al eje $z$.
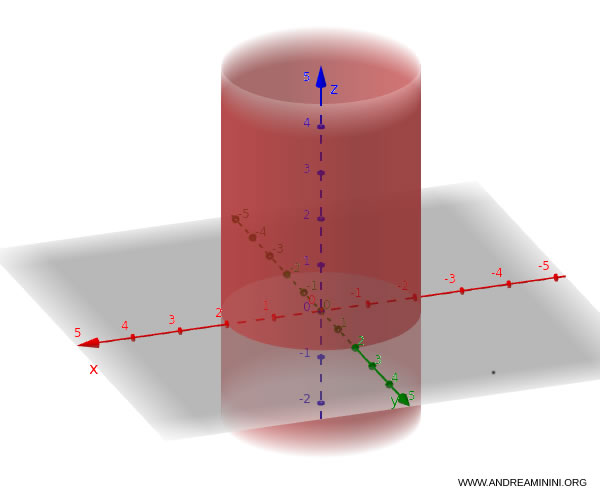
Cilindro hiperbólico
Un cilindro hiperbólico es una superficie tridimensional obtenida al trasladar una hipérbola a lo largo de una dirección paralela a uno de los ejes coordenados. Su ecuación general es: $$\frac{x^2}{a^2} - \frac{y^2}{b^2} = 1$$ Esta fórmula describe una superficie que se prolonga indefinidamente en la dirección del eje $z$.
En otras palabras, para cualquier valor de $z$, los puntos $(x, y)$ cumplen la ecuación de la misma hipérbola en el plano $xy$.
Esta superficie se caracteriza por dos elementos esenciales:
- Directriz: la hipérbola definida en el plano $xy$, cuyas ramas se abren y se separan según sus asíntotas.
- Generatrices: rectas paralelas al eje $z$ a lo largo de las cuales se traslada la directriz, generando toda la superficie.
El cilindro hiperbólico es un ejemplo de superficie reglada, ya que se construye mediante el desplazamiento de una curva plana a lo largo de rectas. Además, es una superficie cilíndrica porque mantiene la misma sección transversal (una hipérbola) en todos los planos paralelos al plano directriz.
La orientación del cilindro viene determinada por la dirección de las generatrices. En este caso, al no depender de $z$, el eje es paralelo al eje $z$.
Cambiando de variables, la misma idea se aplica si el desplazamiento se hace en dirección del eje $x$ o $y$.
Ejemplo. Tomemos la ecuación: $$ \frac{x^2}{2} - \frac{y^2}{4} = 3 $$ La directriz está en el plano $xy$ y la hipérbola se abre en dirección del eje $x$. Esta ecuación puede reescribirse así:
$$ x^2 = 2 \left( 3 + \frac{y^2}{4} \right ) $$
o bien:
$$ y^2 = 4 \left( \frac{x^2}{2} - 3 \right ) $$
Cada punto $(x, y)$ genera una recta vertical, paralela al eje $z$, que forma parte de la superficie cilíndrica.

Cilindro parabólico
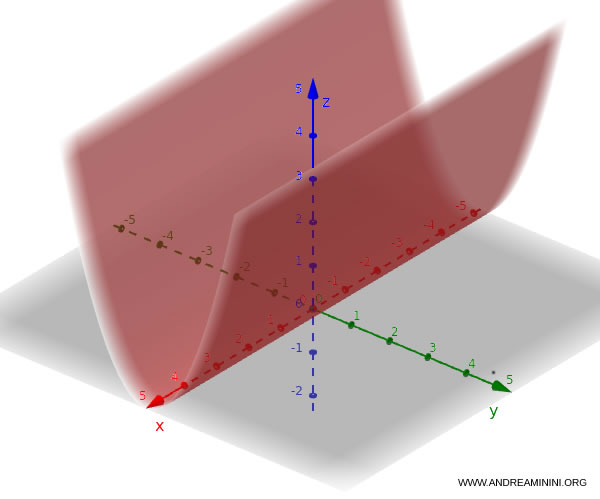
Un cilindro parabólico es una superficie tridimensional generada al trasladar una parábola a lo largo de una dirección paralela a uno de los ejes cartesianos. Su ecuación general es: $$ y = k x^2 $$ con $k$ constante real. En este caso, el eje del cilindro es paralelo al eje $z$.
La ecuación se mantiene válida para cualquier valor de $z$, lo que significa que la superficie se extiende indefinidamente en esa dirección. De ahí que se lo denomine cilindro infinito.
Ejemplo. Consideremos la parábola $ y = x^2 $ como directriz. La superficie generada se describe mediante:
$$y = x^2, \quad z \in \mathbb{R} $$
Esta consiste en infinitas parábolas idénticas en el plano $xy$, replicadas a lo largo del eje $z$.
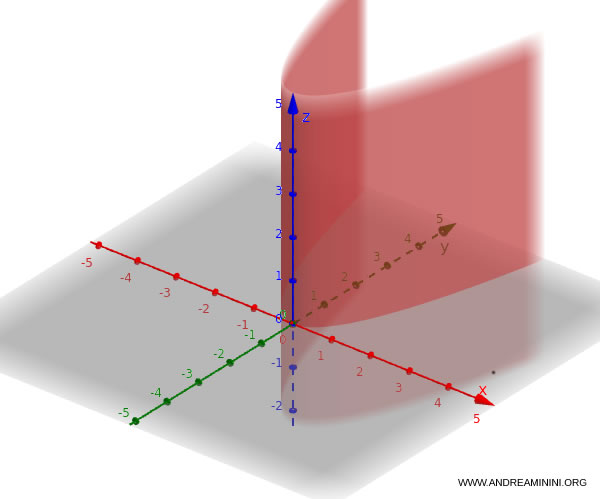
Visualmente, equivale a “deslizar” una parábola en la dirección vertical.
Si la parábola se encuentra en el plano $xz$, la ecuación es:
$$ z = x^2 $$
En ese caso, el eje del cilindro es paralelo al eje $y$.
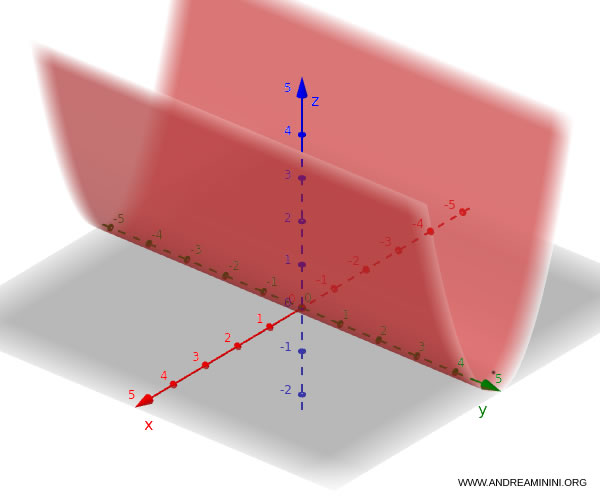
De forma análoga, si la parábola se halla en el plano $yz$, se tiene:
$$ z = y^2 $$
Y el eje del cilindro será paralelo al eje $x$.
Observaciones
A continuación, algunas observaciones relevantes sobre los cilindros:
- Dos cilindros circulares rectos son congruentes si tienen igual altura y el mismo radio de base.
- La intersección de un cilindro recto con un plano que pasa por el eje y es perpendicular a la base da lugar a un rectángulo (o un cuadrado, si el cilindro es equilátero).
- Aunque el cilindro comparte similitudes con el prisma de base poligonal, su base circular le confiere propiedades distintivas como la simetría rotacional.
- Equivalencia de volumen entre prisma y cilindro
Un prisma y un cilindro - cualquiera sea la forma de su base - poseen el mismo volumen si tienen la misma área de base $A$ y altura $h$.
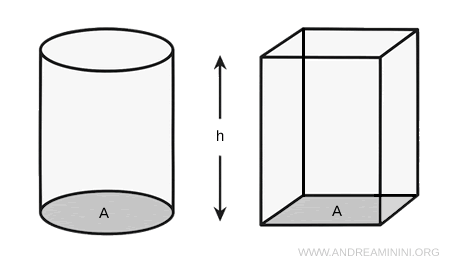
Demostración. En ambos casos, el volumen se calcula con la fórmula: $$ V = A \cdot h $$ donde $A$ es el área de la base y $h$ la altura, medida perpendicularmente entre las bases.
Y así sucesivamente…