Hiperboloide

Un hiperboloide es una superficie cuádrica en el espacio tridimensional que se presenta en dos formas principales: el hiperboloide de una hoja y el hiperboloide de dos hojas, cada una con su propia ecuación característica.

• Hiperboloide de una hoja
  El hiperboloide de una hoja es una superficie continua que se extiende indefinidamente y cuya forma recuerda a un cuello de botella o a una silla de montar. También se conoce como “hiperboloide hiperbólico”. Su ecuación general, de segundo grado, es: $$ \frac{x^2}{a^2} + \frac{y^2}{b^2} - \frac{z^2}{c^2} = 1 $$ donde los parámetros \(a\), \(b\) y \(c\) definen las dimensiones de la superficie en las direcciones de los ejes \(x\), \(y\) y \(z\). Las secciones horizontales (planos de altura constante \(z\)) son elipses, mientras que las secciones verticales (paralelas a los ejes \(x\) o \(y\)) son hipérbolas. Se trata de una superficie unificada, sin interrupciones.
  
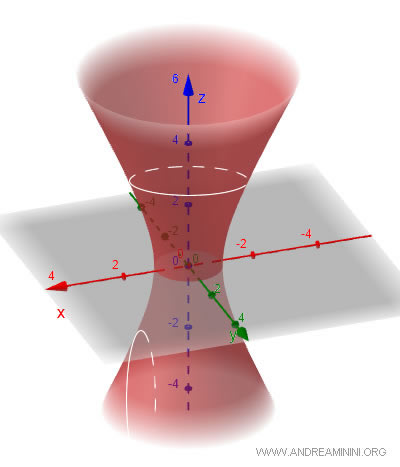
• Hiperboloide de dos hojas
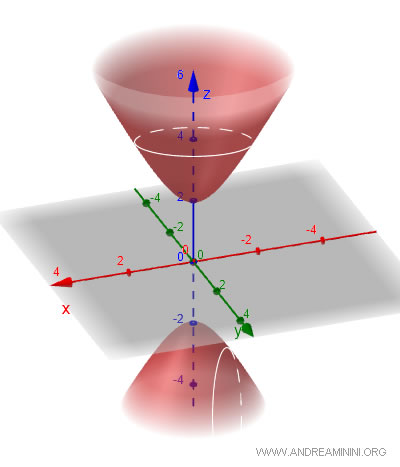
  El hiperboloide de dos hojas está formado por dos superficies separadas y simétricas que se abren en direcciones opuestas desde un punto central. A menudo se le denomina “hiperboloide elíptico”. Su ecuación general es: $$ \frac{x^2}{a^2} + \frac{y^2}{b^2} - \frac{z^2}{c^2} = -1 $$ Nuevamente, los parámetros \(a\), \(b\) y \(c\) determinan el tamaño y la orientación de la superficie. Las secciones horizontales siguen siendo elipses, y las verticales, hipérbolas. A diferencia del caso de una sola hoja, esta superficie consta de dos componentes desconectadas, lo que significa que no es continua.
  

Los hiperboloides son superficies regladas, es decir, pueden generarse mediante el desplazamiento de rectas en el espacio. Esta propiedad los hace especialmente útiles en aplicaciones estructurales y de diseño.

Son ampliamente utilizados en arquitectura e ingeniería para construir estructuras ligeras, estables y resistentes, como torres, cúpulas, cubiertas tensadas o entramados espaciales.

Y así sucesivamente.