Teorema de Tales en el espacio
Un conjunto de planos paralelos \( \pi_1, \pi_2, \pi_3 \) corta dos rectas transversales \( r \) y \( s \), dividiéndolas en segmentos correspondientes que guardan la misma proporción.
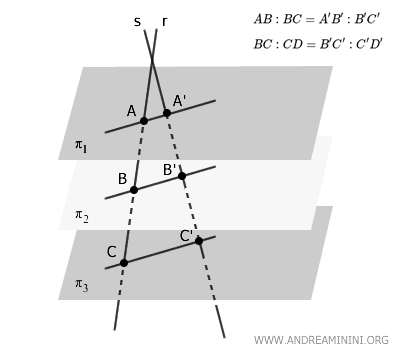
Este resultado no es más que la extensión tridimensional del clásico teorema de Tales en el plano.
En esencia, el teorema de Tales en el espacio establece que la razón entre los segmentos determinados por una familia de planos paralelos se conserva en cualquier par de transversales, ya sean coplanares o alabeadas.
Demostración
Sea un conjunto de planos paralelos \( \pi_1, \pi_2, \dots, \pi_n \).
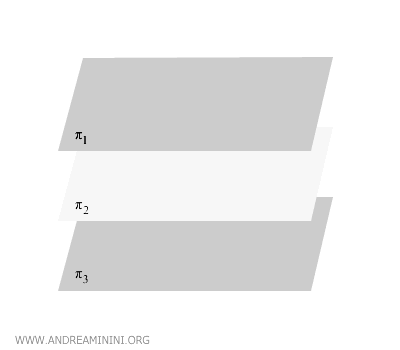
La demostración se divide en dos casos: uno para transversales coplanares y otro para transversales alabeadas (no coplanares).
1] Caso de transversales coplanares
En este caso, las rectas transversales \( r \) y \( s \) están contenidas en un mismo plano.
El plano que contiene a \( r \) y \( s \) corta los planos paralelos a lo largo de rectas paralelas, generando segmentos como \( AA' \), \( BB' \), \( CC' \), etc.
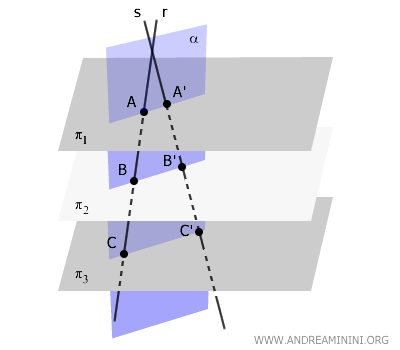
Dado que las rectas \( AA' \), \( BB' \), \( CC' \) son paralelas entre sí y están contenidas en el mismo plano \( \alpha \), que también incluye a las transversales \( r \) y \( s \), se concluye que todas estas rectas son coplanares.
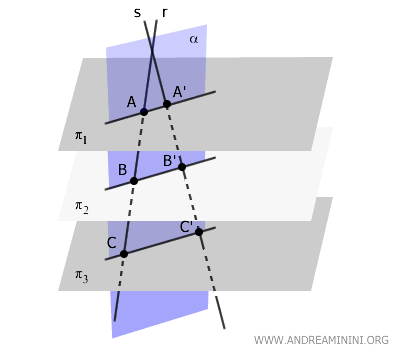
Aplicando el teorema de Tales en el plano, sabemos que dos transversales que cortan un haz de rectas paralelas determinan segmentos proporcionales:
$$ \frac{AB}{BC} = \frac{A'B'}{B'C'} $$
$$ \frac{BC}{CD} = \frac{B'C'}{C'D'} $$
$$ \frac{AC}{BC} = \frac{A'C'}{B'C'} $$
$$ \dots $$
La proporcionalidad se conserva también para cualquier otro par de segmentos determinados por los planos paralelos.
Por lo tanto, el teorema de Tales en el espacio queda demostrado en el caso de transversales coplanares.
2] Caso de transversales alabeadas
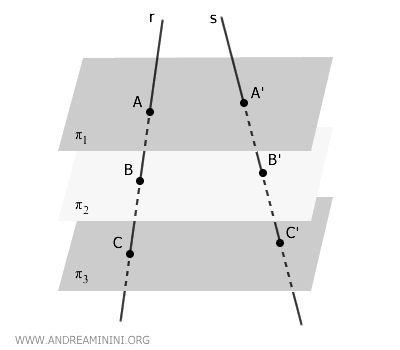
Veamos ahora el caso en que \( r \) y \( s \) son rectas alabeadas, es decir, que no pertenecen a un mismo plano.
Los puntos de intersección entre la recta \( r \) y los planos paralelos se denotan \( A, B, C, \dots \), mientras que los puntos donde \( s \) corta esos mismos planos se nombran \( A', B', C' \).
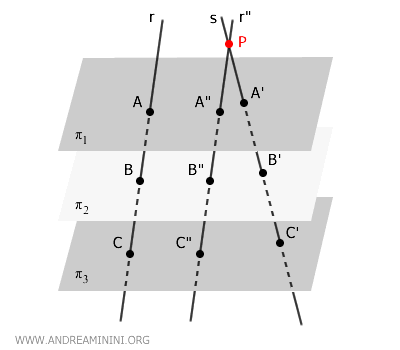
Para relacionar las dos transversales, se introduce una nueva recta \( r'' \), paralela a \( r \), que pasa por un punto \( P \) de la recta \( s \). Esta construcción genera un plano que contiene tanto a \( s \) como a \( r'' \), lo que nos permite aplicar el teorema de Tales en el plano.
Los puntos donde \( r'' \) corta los planos paralelos se designan como \( A'', B'', C'' \).
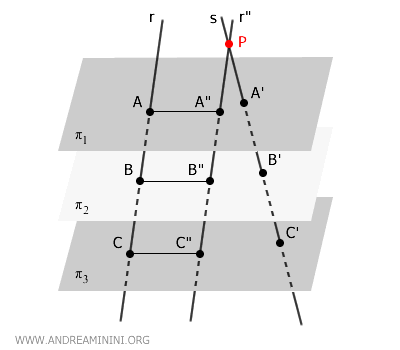
Con esta configuración, los segmentos forman paralelogramos como \( ABB''A'' \) y \( ACC''A'' \).
Al ser paralelogramos, sus lados opuestos son paralelos y congruentes. En particular, \( AB \cong A''B'' \) y \( AC \cong A''C'' \), es decir, tienen la misma longitud.
Las rectas \( r'' \) y \( s \) se cruzan, por lo tanto pertenecen a un mismo plano \( \alpha \), lo que significa que son coplanares.
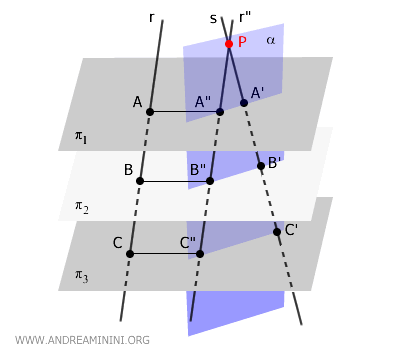
Ahora que \( r'' \) y \( s \) son coplanares, se puede aplicar el teorema de Tales en el plano a estas dos transversales:
$$ \frac{A''B''}{B''C''} = \frac{A'B'}{B'C'} $$
$$ \frac{A''C''}{B''C''} = \frac{A'C'}{B'C'} $$
Dado que \( AB \cong A''B'' \) y \( AC \cong A''C'' \), concluimos que:
$$ \frac{AB}{BC} = \frac{A'B'}{B'C'} $$
$$ \frac{AC}{BC} = \frac{A'C'}{B'C'} $$
Por tanto, el teorema de Tales en el espacio también se cumple cuando las transversales no son coplanares.
Y así sucesivamente.