Sólidos Equidecomponibles

Se dice que dos sólidos son equidecomponibles (o equicomponibles) si pueden dividirse en un número finito de partes tridimensionales tales que cada una de las piezas de un sólido sea congruente con una correspondiente del otro. Es fundamental que dichas piezas sean cuerpos tridimensionales y no meras superficies o líneas.

En términos sencillos: dos sólidos son equidecomponibles si es posible “desmontar” uno en piezas que coincidan exactamente con las del otro, sin superposiciones, huecos ni deformaciones.

Cada parte del primer sólido debe coincidir con la correspondiente del segundo tanto en forma como en tamaño.

No se permite estirar, comprimir ni transformar: se trata de una reconstrucción puramente geométrica.

Los sólidos equidecomponibles deben tener necesariamente el mismo volumen, ya que sus partes congruentes ocupan regiones espaciales idénticas.

Nota. La recíproca no siempre se cumple: dos sólidos pueden tener el mismo volumen sin ser equidecomponibles.

Ejemplo práctico

Consideremos un cubo con lados de 2 cm. Su volumen es de 8 cm³.

Imaginemos que lo descomponemos en ocho cubos más pequeños, cada uno de 1 cm de lado, y luego los reorganizamos para formar otro cubo con el mismo volumen.

Al ensamblar estos ocho cubos unitarios en una nueva configuración, obtenemos un sólido equidecomponible con el original.

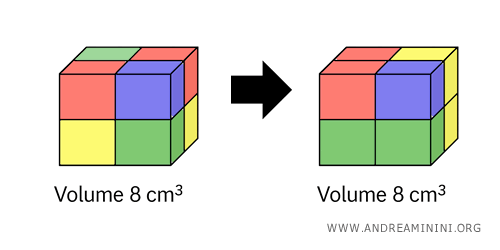
En este caso, los dos sólidos son equidecomponibles porque están formados por el mismo conjunto de piezas congruentes.

Ambos tienen también el mismo volumen: 8 cm³.

Ejemplo 2

Veamos ahora dos prismas rectangulares con base cuadrada:

El primero tiene una base de 2 cm × 2 cm y una altura de 3 cm.

El segundo tiene una base de 1 cm × 1 cm y una altura de 12 cm.

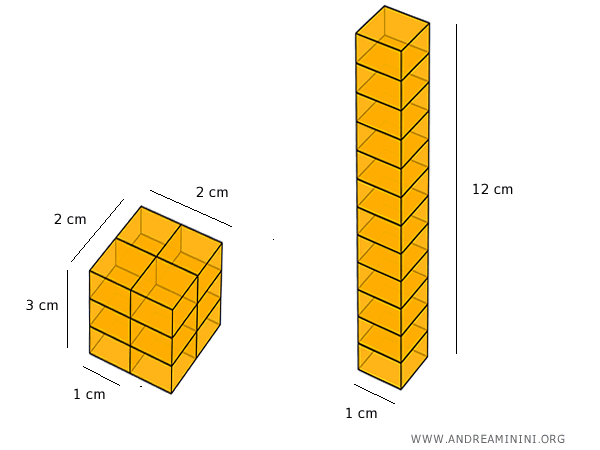
Ambos tienen un volumen de 12 cm³ y son equidecomponibles, ya que pueden dividirse en bloques rectangulares congruentes mediante cortes rectos.

Ejemplo 3

Consideremos ahora una pirámide de base cuadrada de 1 cm de lado y 3 cm de altura, junto a un cubo de 1 cm de lado.

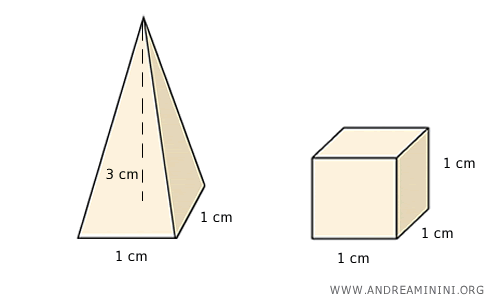
El volumen de la pirámide es:

$$ V_p = \frac{1}{3} l^2 \cdot h = \frac{1}{3} \cdot (1 \ cm)^2 \cdot 3 \ cm = 1 \ cm^3 $$

El cubo también tiene un volumen de 1 cm³.

No obstante, a pesar de tener volúmenes iguales, la pirámide y el cubo no son equidecomponibles.

No existe una manera de descomponer una pirámide en un número finito de partes sólidas congruentes con las de un cubo, al menos dentro del marco de la geometría clásica. Lograrlo requeriría construcciones mucho más abstractas.

Este ejemplo demuestra que la igualdad de volumen no implica necesariamente equidecomponibilidad.

Diferencia entre sólidos equivalentes y equidecomponibles

En geometría, la equidecomponibilidad es una condición más restrictiva que la equivalencia volumétrica.

• Sólidos equivalentes: poseen el mismo volumen, aunque no necesariamente están relacionados geométricamente.
• Sólidos equidecomponibles: además de ser equivalentes en volumen, pueden descomponerse en partes congruentes que permiten reconstruir uno a partir del otro.

La equidecomponibilidad constituye un concepto profundo en geometría: nos lleva más allá del volumen, y nos invita a concebir el espacio como algo susceptible de ser desmontado y reorganizado, como un rompecabezas tridimensional.

Nota. En geometría sólida clásica, demostrar que dos sólidos son equidecomponibles puede ser sumamente complejo. No depende solamente de las medidas externas, sino de su estructura interna.

Teorema de Equidecomponibilidad

Si dos sólidos son equidecomponibles, entonces necesariamente tienen el mismo volumen.

Es decir, la equidecomponibilidad garantiza la equivalencia volumétrica entre sólidos.

Sin embargo, la recíproca no es cierta: dos sólidos pueden tener el mismo volumen y no ser equidecomponibles - como ocurre, por ejemplo, con un cubo y una esfera.

Por tanto, la equidecomponibilidad es una condición más fuerte: no basta con tener el mismo volumen, también es necesario que exista una descomposición finita en partes congruentes que permita reconstruir uno a partir del otro.

Nota. Imagina que construyes una pared con bloques de juguete. Luego desmontas esa pared y usas exactamente los mismos bloques para formar una torre. Aunque las formas sean distintas, ambos cuerpos están formados por los mismos elementos. En geometría sólida, se dice que los dos sólidos son equidecomponibles. Y dado que cada bloque ocupa el mismo volumen, la torre y la pared también son equivalentes en volumen.

El concepto fue introducido - aunque de forma primitiva - por Euclides en los Elementos, Libro XII.

Más adelante fue refinado durante el Renacimiento y formalizado con rigor por Bonaventura Cavalieri, quien desarrolló la idea de comparar volúmenes mediante secciones planas equivalentes, lo que hoy se conoce como el Principio de Cavalieri.

Ejemplo concreto

Consideremos dos sólidos, $\mathbb{U}$ y $\mathbb{V}$, ilustrados en el siguiente diagrama (no incluido aquí).

El sólido $\mathbb{U}$ está compuesto por tres partes: $\mathbb{U}_1$, $\mathbb{U}_2$ y $\mathbb{U}_3$.

Del mismo modo, el sólido $\mathbb{V}$ se compone de: $\mathbb{V}_1$, $\mathbb{V}_2$ y $\mathbb{V}_3$.

Supongamos que se cumple lo siguiente:

$\mathbb{U}_1 \cong \mathbb{V}_1$,

$\mathbb{U}_2 \cong \mathbb{V}_2$,

$\mathbb{U}_3 \cong \mathbb{V}_3$.

Como cada parte de $\mathbb{U}$ es congruente con su respectiva en $\mathbb{V}$, se concluye que los dos sólidos son equidecomponibles.

De acuerdo con el teorema, también deben ser equivalentes, ya que ocupan el mismo volumen en el espacio, aunque sus formas globales sean distintas.

El Invariante de Dehn

En geometría tridimensional, la igualdad de volumen no garantiza la equidecomponibilidad.

El principal obstáculo es una magnitud matemática conocida como el invariante de Dehn, introducida en 1900 por el matemático alemán Max Dehn. Este invariante actúa como barrera fundamental a la posibilidad de descomponer ciertos sólidos en partes congruentes.

El invariante de Dehn recoge información sobre los ángulos diedros - los ángulos entre caras adyacentes - y cómo se combinan a lo largo del sólido.

Si dos poliedros tienen invariantes de Dehn distintos, entonces no pueden ser equidecomponibles.

Este resultado demuestra, por ejemplo, que no es posible cortar un cubo en un número finito de partes congruentes y reensamblarlas para obtener un tetraedro del mismo volumen, ya que sus invariantes de Dehn no coinciden.

En resumen:

• En dos dimensiones, cualquier par de polígonos con igual área es equidecomponible (teorema de Bolyai - Gerwien).
• En tres dimensiones, el invariante de Dehn impone restricciones severas a la posibilidad de equidecomposición.

Esto marca uno de los límites de la equidecomponibilidad. Más allá de él se extienden fronteras aún más complejas, que involucran teoría de la medida, descomposiciones no medibles y nociones abstractas de congruencia en espacios generales.

Notas

Algunas consideraciones adicionales sobre la equidecomponibilidad:

• La paradoja de Banach - Tarski
  Esta famosa paradoja afirma que, bajo ciertos supuestos teóricos (en particular, aceptando el Axioma de Elección), es posible dividir una esfera sólida en un número finito de subconjuntos que, reordenados mediante rotaciones y traslaciones, dan lugar a dos esferas idénticas a la original.

  Nota. Esta paradoja no contradice la geometría clásica, simplemente no se enmarca en ella. Las “piezas” que intervienen no son cuerpos geométricos en sentido tradicional: son conjuntos no medibles, carentes de volumen definido, construidos con herramientas puramente lógicas. Por eso, la paradoja de Banach - Tarski no constituye un ejemplo válido de equidecomponibilidad. No se basa en piezas congruentes, no conserva la medida y opera completamente fuera de la teoría clásica de la disección. Es un ejemplo extremo de lo que puede ocurrir cuando se llevan los conceptos de teoría de conjuntos más allá de la intuición.

Y así sucesivamente.