Sólidos Equivalentes

Decimos que dos sólidos son equivalentes cuando poseen el mismo volumen, aunque sus formas sean completamente distintas. \[ V_A = V_B \] Aquí, \( V_A \) y \( V_B \) representan los volúmenes de ambos sólidos.

Este concepto se refiere exclusivamente a la cantidad de espacio que ocupa un sólido, sin implicar nada respecto a su forma ni a su área superficial.

Dos cuerpos pueden presentar apariencias totalmente diferentes y, sin embargo, ocupar exactamente el mismo volumen.

Así, la equivalencia no significa que los sólidos tengan la misma altura, base o superficie, sino únicamente que encierran el mismo volumen.

Un Ejemplo Práctico

Un cubo con aristas de 3 cm tiene un volumen de 27 cm³:

\[ V = 3^3 = 27 \ cm^3 \]

Un prisma rectangular cuya base mide 3 cm × 3 cm y cuya altura es de 3 cm también posee un volumen de 27 cm³:

\[ V = 3^3 = 27 \ cm^3 \]

Del mismo modo, un cilindro con área de base de 9 cm² y altura de 3 cm tiene el mismo volumen:

\[ V = 9 \cdot 3 = 27 \ cm^3 \]

Se trata, sin duda, de sólidos con formas diferentes, pero equivalentes en cuanto a volumen.

Transformaciones que Conservan el Volumen

Muchos sólidos pueden transformarse en otros sin que su volumen se modifique.

Estas transformaciones consisten en desplazar, cortar y reordenar las partes que integran el sólido.

Ejemplo

Un prisma triangular puede dividirse en tres pirámides de igual volumen. Reorganizando dichas pirámides, se obtiene un sólido volumétricamente equivalente al prisma original.

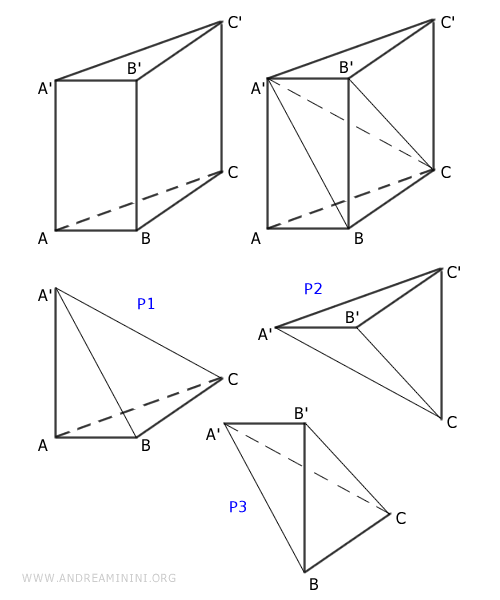
Nota. Las pirámides P1 y P2 comparten una base congruente $ ABC = A'B'C' $ y la misma altura $ AA' = CC' $, por lo que son equivalentes. Las pirámides P2 y P3 poseen bases congruentes $ BCC' = BCB' $ y una altura común $ A'B' $, lo que las hace también equivalentes. Por la propiedad transitiva, P1 y P3 deben ser igualmente equivalentes entre sí.

El volumen de una pirámide se calcula mediante la fórmula:

\[ V = \frac{1}{3} \cdot \text{base} \cdot \text{altura} \]

Mientras que el volumen de un prisma se determina así:

\[ V = \text{base} \cdot \text{altura} \]

Esto demuestra que, cuando base y altura son idénticas, una pirámide tiene un tercio del volumen de un prisma.

Por tanto, al reunir tres pirámides idénticas se forma un prisma de volumen equivalente, lo que prueba que ambos sólidos son equivalentes.

Equivalencia vs. Congruencia

Es importante distinguir entre los conceptos de equivalencia y congruencia.

• Congruencia: significa que los sólidos tienen la misma forma y tamaño. Por ejemplo, dos cubos idénticos son congruentes y, por tanto, equivalentes.
  
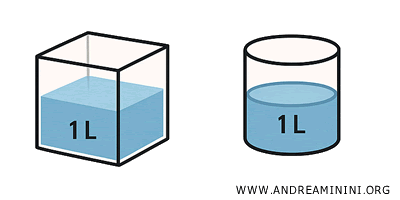
• Equivalencia: implica que los sólidos poseen el mismo volumen, aunque sus formas sean diferentes. Por ejemplo, un cubo y un cilindro con volúmenes iguales son equivalentes, aunque no congruentes.
  

En otras palabras, “congruentes” significa que son idénticos en todos los aspectos - forma, dimensiones y volumen - mientras que “equivalentes” se refiere únicamente a que encierran el mismo volumen, aunque sus formas sean distintas.

Por tanto, cuando se dice que dos sólidos son “equivalentes”, no significa que sean idénticos en apariencia ni que puedan superponerse perfectamente; simplemente indica que ocupan el mismo espacio.

Notas

Algunas reflexiones y observaciones adicionales sobre el concepto de equivalencia de sólidos.

• La suma o diferencia de sólidos congruentes o equivalentes produce sólidos de igual volumen
  Cuando un sólido se forma sumando o restando otros sólidos congruentes (idénticos en forma y tamaño) o equivalentes (idénticos en volumen), los sólidos resultantes también comparten el mismo volumen, es decir, son equivalentes desde un punto de vista volumétrico.
  

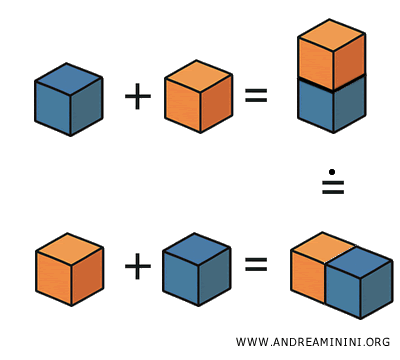
  Ejemplo. Imaginemos que tengo dos cubos idénticos y elimino de ambos la misma pirámide. Los sólidos que quedan serán equivalentes. Si luego añado el mismo cilindro a ambos, las figuras resultantes seguirán teniendo el mismo volumen y, por tanto, serán equivalentes.

• Principio de Exclusión
  Según este postulado - conocido como principio de exclusión - , dados dos sólidos A y B, solo puede cumplirse uno de estos tres casos:
  • A y B son equivalentes: $ A \doteq B $, es decir, tienen el mismo volumen.
  • A domina a B: $ A > B $. En este caso, A tiene mayor volumen que B.
  • A es menor que B: $ A < B $. En este caso, A tiene menor volumen que B.
  Estos casos son mutuamente excluyentes.

  Nota. Esta clasificación tripartita - equivalente, dominante, subordinado - parte del supuesto de que siempre es posible comparar de forma inequívoca dos sólidos cualesquiera. Sin embargo, esto pasa por alto un problema frecuente: dos objetos pueden no ser comparables bajo un único criterio, sobre todo cuando intervienen atributos múltiples e inconmensurables, como volumen, simetría, complejidad geométrica, valor estético o funcionalidad. El hecho de tener varios criterios no garantiza, por sí solo, la posibilidad de establecer un orden coherente. A menudo, las comparaciones se vuelven imposibles. Forzar todas las relaciones a un orden total supone simplificar en exceso la complejidad inherente a la realidad. Por ejemplo, un cubo de mármol y uno de madera pueden tener el mismo volumen, pero diferir radicalmente en peso, densidad, coste, durabilidad o uso previsto, lo que los hace incomparables en un sentido relevante. De manera similar, una esfera y un cubo de igual volumen difieren en superficie, aerodinámica y estabilidad - es decir, en propiedades que van más allá de la mera medida. Reducir estas diferencias multifacéticas a una sola dimensión evaluativa es una simplificación arbitraria.

• Postulado de De Zolt
  El postulado de De Zolt establece que un sólido no puede ser equivalente a ninguna de sus partes propias; es decir, no puede tener el mismo volumen que una porción contenida en su interior.
• Principio de Cavalieri
  Si las secciones transversales de dos sólidos son iguales a cada altura en una misma dirección, entonces ambos sólidos tienen el mismo volumen.

Y así sucesivamente.