Un sólido generado al sustraer dos conos de un cilindro
Este sólido geométrico se obtiene al eliminar dos conos idénticos de un cilindro equilátero que encierra perfectamente una esfera.
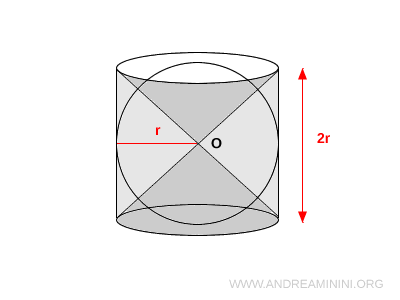
Aunque su construcción es sencilla, la figura resultante presenta propiedades geométricas notables, especialmente en lo que respecta a su simetría y volumen.
Cómo se construye el sólido
Partimos de una esfera centrada en el punto O y de radio $R$.
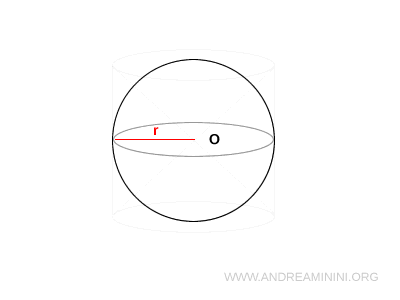
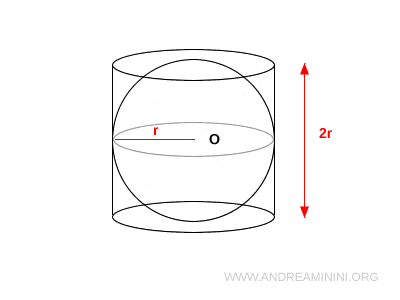
La esfera se inscribe en un cilindro equilátero, es decir, un cilindro cuya altura $h$ coincide con el diámetro de su base $r$. Por tanto:
- Altura del cilindro: $h = 2R$
- Radio de la base: $r = R$
Después se construyen dos conos idénticos con vértice en el punto O y cuyas bases coinciden con las caras superior e inferior del cilindro.
Cada cono tiene:
- Altura: $R$
- Radio de la base: $R$
Se sustraen ambos conos del volumen total del cilindro.
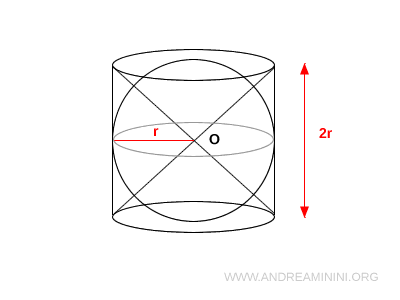
La figura final es un cilindro cuyos extremos han sido recortados simétricamente por dos conos opuestos: una forma equilibrada y sorprendentemente armónica.
Volumen del sólido
El sólido obtenido al sustraer los dos conos del cilindro tiene exactamente el mismo volumen que la esfera inscrita en su interior.
El volumen del cilindro equilátero es:
$$ V_{\text{cyl}} = \pi R^2 \cdot 2R = 2\pi R^3 $$
El volumen de un cono con base y altura iguales a $R$ es:
$$ V_{\text{cone}} = \frac{1}{3} \pi R^2 \cdot R = \frac{1}{3} \pi R^3 $$
Al eliminar dos conos, el volumen total sustraído será:
$$ 2 \cdot V_{\text{cone}} = \frac{2}{3} \pi R^3 $$
Por tanto, el volumen del sólido resultante es:
$$ V_{\text{solid}} = V_{\text{cyl}} - 2 \cdot V_{\text{cone}} = 2\pi R^3 - \frac{2}{3} \pi R^3 = \frac{4}{3} \pi R^3 $$
Y este resultado coincide exactamente con el volumen de una esfera de radio $R$:
$$ V_{\text{sphere}} = \frac{4}{3} \pi R^3 $$
Ejemplo
Si el radio de la esfera es $R = 3$ cm, el volumen del sólido será:
$$ V = \frac{4}{3} \pi (3)^3 = \frac{4}{3} \pi \cdot 27 = 36\pi \approx 113.1 \, \text{cm}^3 $$
Este ejemplo pone de relieve un hecho sorprendente: aunque el sólido se construye a partir de figuras simples, su volumen es exactamente igual al de la esfera que contiene. Un resultado inesperado, pero completamente riguroso desde el punto de vista matemático.
Nota. Este sólido ofrece una magnífica ilustración del principio de comparación de volúmenes, base fundamental del cálculo integral y estrechamente relacionado con el método de los indivisibles desarrollado por Arquímedes. Al descomponer los sólidos en elementos infinitesimales - como láminas o segmentos - y compararlos uno a uno, es posible demostrar que, si cada par de elementos correspondientes tiene la misma medida, entonces los volúmenes totales también deben coincidir. Este es, en esencia, el Principio de Cavalieri.
Demostración
Consideremos un cilindro circular recto de altura $2r$ y radio $r$, apoyado sobre un plano base $p$. En su interior se encuentra una esfera inscrita y dos conos idénticos con vértice común en el punto $O$ (centro de la esfera) y cuyas bases coinciden con las del cilindro.
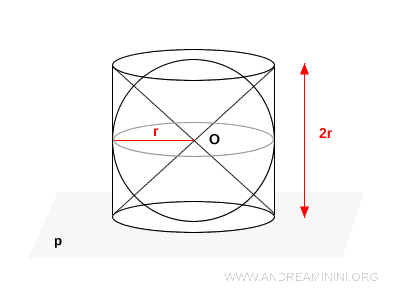
Ahora se corta el cilindro con un plano $p'$ paralelo a la base, situado a una distancia vertical $h$ del centro $O$ de la esfera.
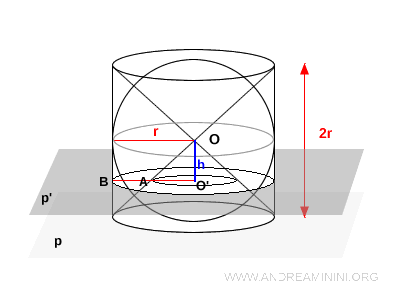
La intersección del plano $p'$ con uno de los conos (la parte sustraída del cilindro) es un círculo de radio $h$. Esto se deduce del triángulo $OO'A$, que es isósceles y rectángulo: como $OO' = O'A$, ambos catetos miden $h$, por tanto $O'A = h$.
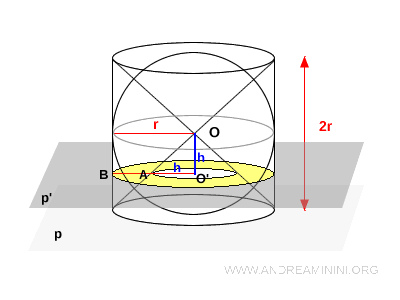
A la altura $h$, la sección horizontal del sólido (cilindro menos dos conos) es una corona circular: el radio exterior es $r$ (proveniente del cilindro) y el interior es $h$ (proveniente del cono).
El área de esta corona circular es:
$$ A_c = \pi r^2 - \pi h^2 = \pi (r^2 - h^2) $$
Veamos ahora lo que ocurre con la esfera inscrita.
Ese mismo plano $p'$ corta la esfera en un círculo. El radio de ese círculo es $O'C$, donde $C$ es un punto sobre la superficie de la esfera.
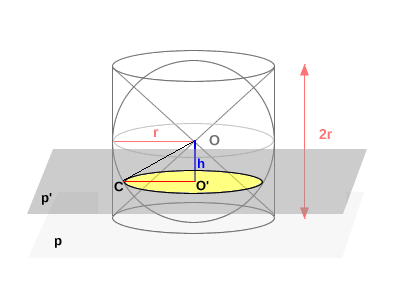
En el triángulo $O'OC$, rectángulo en $O'$, se aplica el teorema de Pitágoras:
$$ O'C^2 = OC^2 - OO'^2 = r^2 - h^2 $$
Así, el área del círculo generado por la intersección entre la esfera y el plano $p'$ es:
$$ A_s = \pi \cdot O'C^2 = \pi (r^2 - h^2) $$
Es decir, a cualquier altura $h$, la sección horizontal de la esfera tiene exactamente la misma área que la del sólido (cilindro menos dos conos).
Según el Principio de Cavalieri, si dos sólidos tienen la misma altura y sus secciones horizontales coinciden a cada nivel, entonces tienen el mismo volumen.
Por tanto, el sólido generado al sustraer dos conos de un cilindro y la esfera inscrita tienen volúmenes iguales.
Y con esto queda demostrada la igualdad.
Y así sucesivamente.