Pirámides
Una pirámide es un poliedro que se genera cuando un ángulo sólido es seccionado por un plano que corta todas sus aristas. La figura resultante de dicha sección se denomina base de la pirámide, y puede adoptar distintas formas poligonales. El vértice del ángulo sólido pasa a ser el vértice de la pirámide.
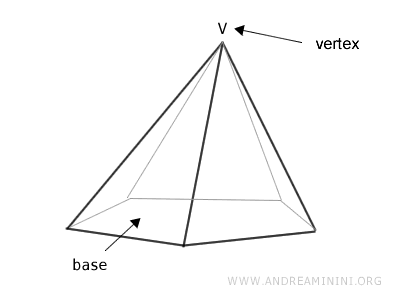
La base de la pirámide es un polígono, mientras que sus caras laterales tienen forma triangular.
Las aristas que delimitan la base se denominan aristas de la base, y las que unen la base con el vértice se llaman aristas laterales.
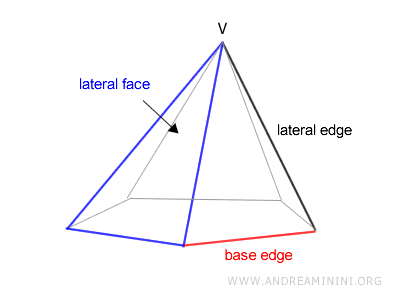
Una característica fundamental de la pirámide es su altura, que corresponde a la distancia perpendicular que hay desde el vértice hasta el plano de la base.
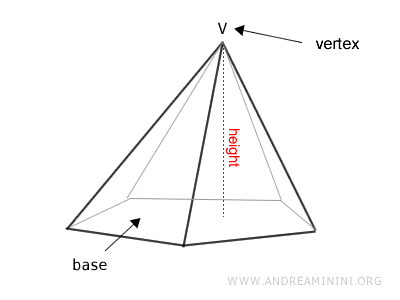
Según el número de lados que tenga su base, una pirámide puede ser triangular, cuadrangular, pentagonal, entre otras.
En toda pirámide, el número de vértices coincide con el número de caras, contando la base. Además, una pirámide siempre tiene al menos cuatro caras. La pirámide con menor número de caras es el tetraedro, formado por cuatro caras triangulares.
Tipos de Pirámides
Podemos distinguir diferentes tipos de pirámides:
- Pirámides con Base Triangular o Cuadrada
La base de una pirámide puede ser un triángulo, un cuadrilátero o cualquier otro polígono, ya sea regular o irregular. Si la base es un triángulo, hablamos de una pirámide triangular. Cuando la base es un cuadrado, se denomina específicamente pirámide de base cuadrada. De forma más general, si la base es cualquier tipo de cuadrilátero, recibe el nombre de pirámide cuadrangular. Esta clasificación se extiende, de igual modo, a pirámides cuyas bases tienen otras formas poligonales.
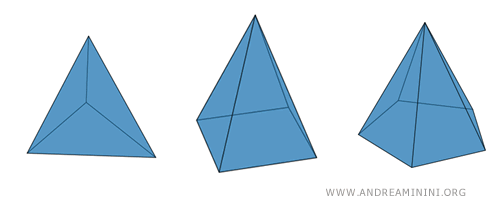
- Pirámide Recta
Una pirámide se denomina pirámide recta cuando su base ABCD puede inscribirse en una circunferencia, y su vértice (V) se encuentra exactamente sobre el centro (O) del circuncírculo de la base.
Es decir, el vértice de la pirámide coincide con la proyección ortogonal del centro del circuncírculo de la base. En las pirámides rectas, la altura es perpendicular al centro (O) de la base (segmento OV). Las alturas de las caras laterales de una pirámide recta se denominan apotemas.
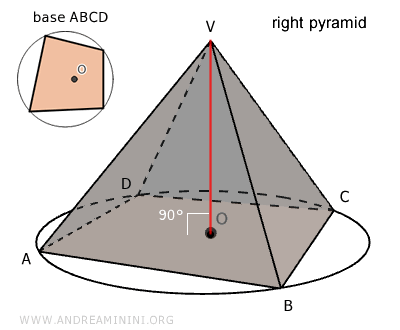
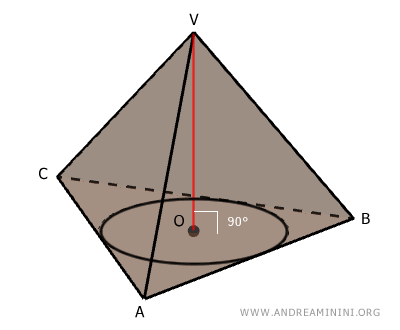
Otra forma de definir una pirámide recta es cuando puede inscribirse una circunferencia en su base, y el centro O de esa circunferencia coincide con la proyección ortogonal del vértice V sobre el plano de la base.
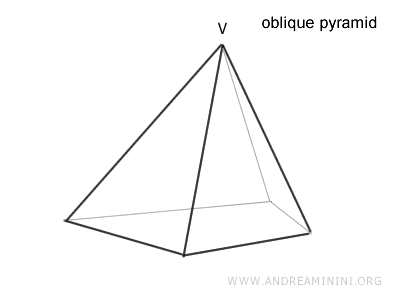
Toda pirámide que no sea recta se denomina pirámide oblicua.
- Pirámide Regular
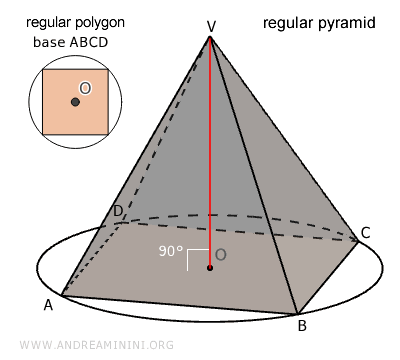
Una pirámide regular es una pirámide recta cuya base ABCD es un polígono regular.
Al ser la base un polígono regular, puede inscribirse y circunscribirse en una circunferencia. Por esta razón, todas las caras laterales de la pirámide son triángulos isósceles congruentes, con la misma altura (apotema). Además, al tratarse de una pirámide recta, la altura de la pirámide pasa por el centro (O) de la base (segmento OV).
- Tronco de Pirámide
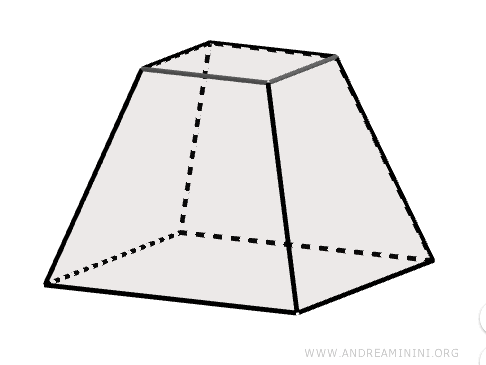
El tronco de una pirámide es un sólido que se obtiene al cortar una pirámide mediante un plano paralelo a su base.
Teorema de la Apotema en una Pirámide Recta
En una pirámide recta, las alturas de las caras laterales (apotemas) son congruentes, es decir, VD ≅ VE ≅ VF, y pasan por los puntos de tangencia D, E y F, donde los lados de la base tocan la circunferencia inscrita.
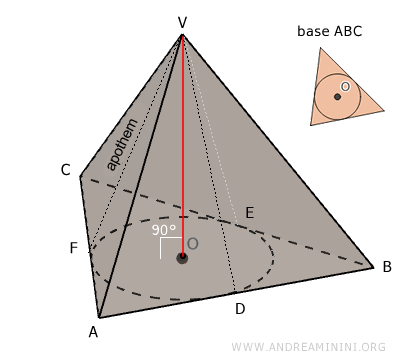
En el ejemplo anterior, las apotemas son los segmentos VD, VE y VF, y todas ellas son congruentes.
$$ \overline{VD} \cong \overline{VE} \cong \overline{VF} $$
Este resultado resulta muy útil para calcular las propiedades métricas de las pirámides.
Fórmulas
Volumen de una Pirámide
El volumen \( V \) de una pirámide se determina con la siguiente fórmula:
$$ V = \frac{1}{3} \cdot (\text{área de la base}) \cdot (\text{altura}) $$
Esta expresión es válida sin importar la forma que tenga la base.
Por tanto, calcular el volumen de una pirámide es bastante sencillo siempre que se conozcan el área de la base y la altura de la figura.
Nota: El volumen de una pirámide es un tercio del producto entre el área de la base y la altura, ya que cualquier pirámide es equivalente a un tercio de un prisma con la misma base y altura. Consulta sólidos equivalentes.
Área Lateral
El área lateral de una pirámide corresponde a la suma de las áreas de sus caras laterales.
En el caso de una pirámide regular, el área lateral se obtiene multiplicando el semiperímetro (p) de la base por la apotema (a).
$$ A_L = p \cdot a $$
Área Total
El área total de una pirámide es la suma de las áreas de todas sus caras, incluyendo la base.
$$ A = A_L + A_B $$
Donde AL es el área lateral y AB el área de la base.
Ejemplo. En una pirámide recta con base cuadrada, su desarrollo plano está formado por un cuadrado (la base) y cuatro triángulos isósceles iguales, cada uno con una altura igual a la apotema (a).
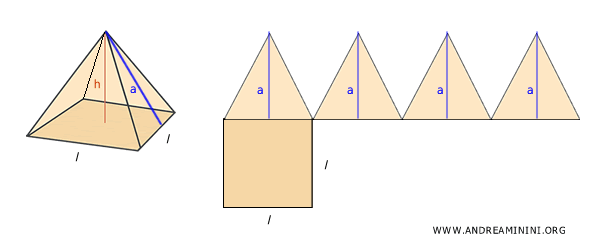
El área lateral de la pirámide se calcula sumando las áreas de las cuatro caras triangulares: $$ A_l = \frac{1}{2} l \cdot a + \frac{1}{2} l \cdot a + \frac{1}{2} l \cdot a + \frac{1}{2} l \cdot a $$ lo cual se simplifica en: $$ A_l = 4 \cdot \frac{1}{2} l \cdot a $$ Dado que el perímetro de la base es $ P = 4l $, podemos expresar la fórmula así: $$ A_l = \frac{1}{2} P \cdot a $$ Y utilizando el semiperímetro $ p = \frac{1}{2} P $, se obtiene: $$ A_l = p \cdot a $$ Es decir, el área lateral es igual al semiperímetro multiplicado por la apotema. El área total se calcula simplemente sumando el área lateral y el área de la base: $$ A_t = A_b + A_l = A_b + p \cdot a $$
Notas Adicionales
A continuación, algunas notas adicionales sobre las pirámides:
- Tronco de Pirámide
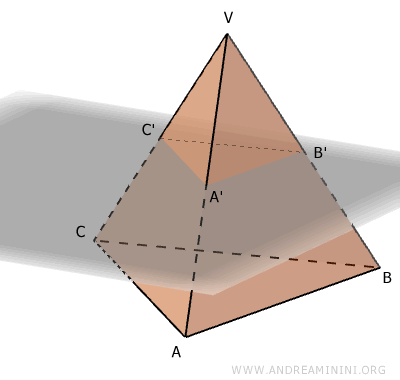
Un plano paralelo a la base que corta la pirámide a una altura h la divide en dos partes: la superior sigue siendo una pirámide A'B'C'V, mientras que la inferior se convierte en un tronco de pirámide de altura h.
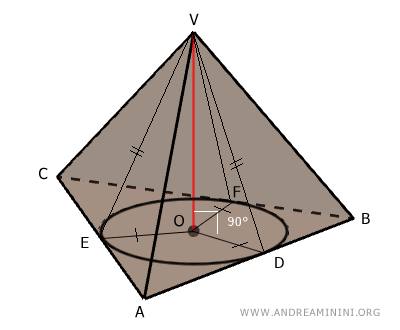
- Teorema de las Alturas de las Caras Laterales de una Pirámide Recta
En una pirámide recta, las alturas (apotemas) de las caras laterales son todas congruentes y se intersectan con la base en los puntos donde la circunferencia inscrita es tangente a sus lados.
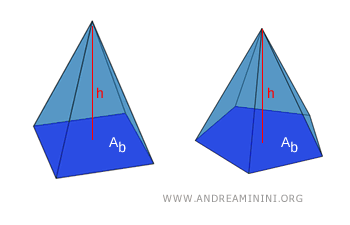
- Pirámides con Volúmenes Iguales
Dos pirámides que tienen áreas de base iguales y la misma altura poseen el mismo volumen. En otras palabras, si dos pirámides comparten la misma área de base $ A_b $ y la misma altura $ h $, sus volúmenes serán idénticos, sin importar la forma de sus bases ni la inclinación de sus caras.
Demostración. Este resultado se deduce directamente de la fórmula del volumen de una pirámide: $$ V = \frac{1}{3} \cdot \text{área de la base} \cdot \text{altura} $$ Dado que el volumen depende únicamente del área de la base y de la altura, cualquier par de pirámides con esos mismos valores tendrá el mismo volumen.
- Una pirámide tiene exactamente un tercio del volumen de un prisma con la misma base y altura
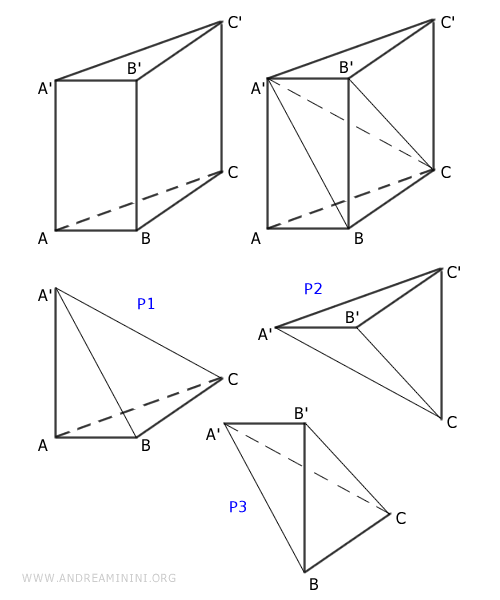
Cuando una pirámide y un prisma tienen bases congruentes y la misma altura, el volumen de la pirámide es exactamente un tercio del volumen del prisma.Ejemplo. Un prisma triangular con base ABC puede descomponerse en tres pirámides de igual volumen: P1, P2 y P3.
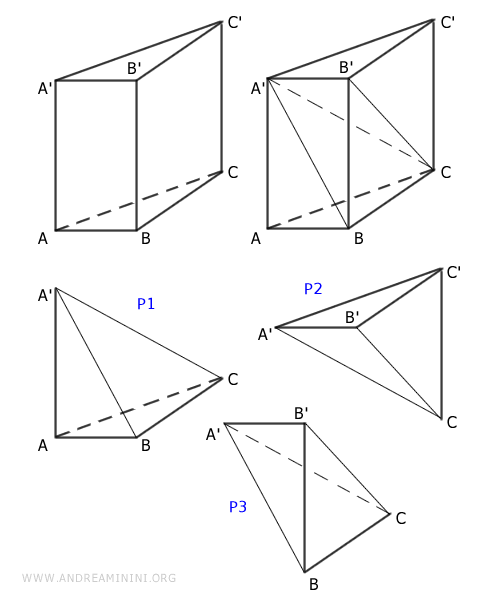
Las pirámides P1 y P2 tienen bases congruentes, $ ABC \cong A'B'C' $, y alturas iguales, $ AA' \cong CC' $, por lo que tienen el mismo volumen: $$ P1 \doteq P2 $$ De forma análoga, las pirámides P2 y P3 comparten bases congruentes, $ BCC' \cong BCB' $, y una altura común, $ A'B' $, por lo que también son equivalentes en volumen: $$ P2 \doteq P3 $$ Por transitividad, P1 y P3 deben ser asimismo equivalentes en volumen: $$ P1 \doteq P2 \doteq P3 \Rightarrow P1 \doteq P3 $$ Así, las tres pirámides que se generan a partir del prisma ocupan exactamente un tercio de su volumen total. El volumen de una pirámide viene dado por la fórmula: \[ V = \frac{1}{3} \cdot \text{base} \cdot \text{altura} \] mientras que el volumen de un prisma es: \[ V = \text{base} \cdot \text{altura} \] Por tanto, cuando ambos sólidos comparten la misma área de base y altura, el volumen de la pirámide es exactamente un tercio del volumen del prisma. - Equivalencia de Volúmenes entre una Pirámide y un Cono
Una pirámide y un cono que tienen bases de igual área y la misma altura poseen exactamente el mismo volumen. En otras palabras, si una pirámide y un cono tienen la misma área de base y altura, sus volúmenes coinciden. Esto se debe a que la fórmula del volumen es esencialmente idéntica para ambos cuerpos: $$ V = \frac{1}{3} \cdot \text{área de la base} \cdot \text{altura} $$ Así, cuando coinciden la base y la altura, también coincide el volumen.Demostración. Consideremos una pirámide y un cono situados sobre el mismo plano $ \alpha $, con igual área de base ($ S = S' $) y la misma altura ($ AB \cong CD $).

Para comparar ambos sólidos, trazamos un segundo plano $ \alpha' $ paralelo a la base ($ \alpha' \parallel \alpha $), que corta tanto a la pirámide como al cono, generando secciones paralelas a sus respectivas bases. Sea $ S_p $ el área de la sección de la pirámide, y $ S_c $ la del cono.

Por las propiedades de los sólidos con bases poligonales y circulares (como un tronco de pirámide o un tronco de cono), sabemos que, al cortar un sólido con un plano paralelo a su base, la razón entre el área de la base $ S $ y el área de la sección $ S_p $ es el cuadrado de la razón de semejanza: $$ \frac{S}{S_p} = \left( \frac{AB}{A'B} \right)^2 \quad \text{(pirámide)} $$ $$ \frac{S'}{S_c} = \left( \frac{CD}{C'D} \right)^2 \quad \text{(cono)} $$ Dado que $ AB = CD $ y $ S = S' $ por hipótesis, se cumple que: $$ \frac{S}{S_c} = \left( \frac{AB}{C'D} \right)^2 \quad \text{(cono)} $$ Y puesto que $ A'B = C'D $, las razones de semejanza son iguales: $$ \frac{S}{S_c} = \left( \frac{AB}{A'B} \right)^2 \quad \text{(cono)} $$ En consecuencia, las secciones $ S_p $ y $ S_c $ tienen la misma área: $$ \frac{S}{S_p} = \frac{S}{S_c} \quad \Rightarrow \quad S_p = S_c $$ Esto se cumple para cualquier plano paralelo a la base; es decir, todas las secciones horizontales de la pirámide y del cono poseen la misma área. Por el principio de Cavalieri, se concluye que la pirámide y el cono tienen el mismo volumen.
Y así sucesivamente.