Teorema de las Apotemas en una Pirámide Recta
En una pirámide recta, las alturas de las caras laterales (apotemas) son congruentes y pasan por los puntos donde la circunferencia inscrita es tangente a los lados de la base.
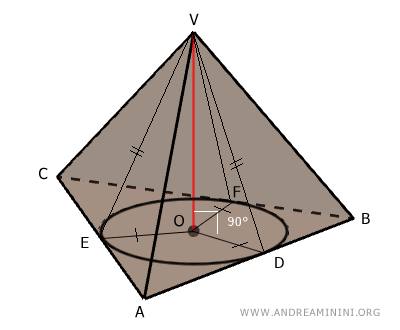
Las alturas de las caras laterales son los segmentos perpendiculares que se trazan desde el vértice de la pirámide hasta los lados de la base.
Este teorema establece que dichas alturas son todas congruentes y se intersecan con la base en los puntos de tangencia entre la circunferencia inscrita y los lados de la base.
¿Por qué es relevante?
Este resultado garantiza que las caras laterales de una pirámide recta poseen simetría perfecta y proporciona un método sencillo para calcular sus alturas cuando se conoce el radio de la circunferencia inscrita.
Nota. En particular, si la base es un polígono regular, las longitudes de las apotemas pueden obtenerse mediante fórmulas geométricas simples.
Demostración
Consideremos una pirámide recta.
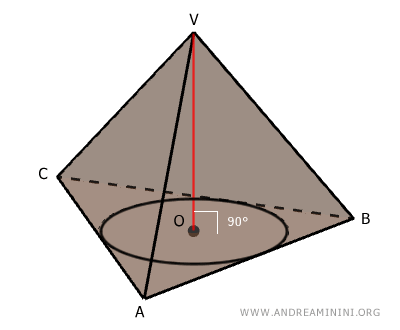
Por definición, el segmento \( OV \) es perpendicular al plano de la base \( ABC \) de la pirámide.
A continuación, tracemos los segmentos que unen el centro de la circunferencia inscrita con los puntos de tangencia \( D, E \) y \( F \).
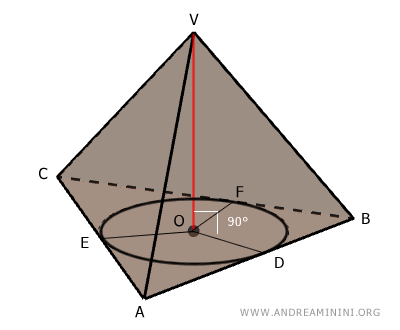
Como se trata de radios de la misma circunferencia, los segmentos \( OD, OE \) y \( OF \) son congruentes.
$$ OD \cong OE \cong OF $$
Además, dado que \( D, E \) y \( F \) son puntos de tangencia, estos radios son perpendiculares a los lados correspondientes de la base:
$$ OD \perp AB $$
$$ OE \perp AC $$
$$ OF \perp BC $$
Ahora tracemos los segmentos que unen cada punto de tangencia \( D, E \) y \( F \) con el vértice \( V \) de la pirámide.
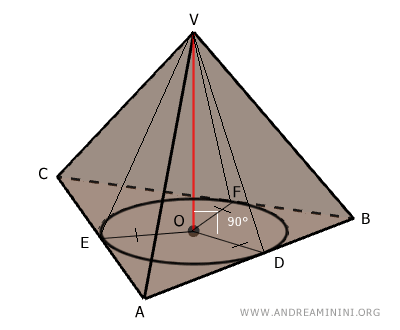
Por el Teorema de las Tres Perpendiculares, dado que \( OV \) es perpendicular al plano de la base \( ABC \) y \( OD \) es perpendicular a \( AB \), se concluye que \( VD \), contenido en la cara lateral, también es perpendicular a \( AB \).
$$ VD \perp AB $$
Por tanto, \( VD \) es la altura de la cara lateral \( ABV \).
El mismo razonamiento se aplica a las alturas \( VE \) y \( VF \) de las demás caras laterales:
$$ VE \perp AC $$
$$ VF \perp BC $$
Consideremos ahora los triángulos \( OVD \) y \( OVE \). Ambos comparten el lado \( OV \), tienen lados congruentes \( OD \cong OE \), y presentan un ángulo recto comprendido entre esos lados. Por el criterio de congruencia Lado-Ángulo-Lado (LAL), dichos triángulos son congruentes:
$$ OVD \cong OVE $$
Como los triángulos congruentes tienen partes correspondientes iguales, se deduce que:
$$ VD \cong VE $$
Por lo tanto, las alturas de estas dos caras laterales son iguales.

Repitiendo este mismo razonamiento, se concluye que todas las apotemas laterales, incluida \( VF \), son congruentes.
En consecuencia, hemos demostrado que, en una pirámide recta, las alturas de todas sus caras laterales son congruentes.
Q.E.D. (Quod Erat Demonstrandum)