Prismas

Un prisma es un poliedro que se caracteriza por tener dos caras paralelas y congruentes, denominadas bases, mientras que sus demás caras son paralelogramos.

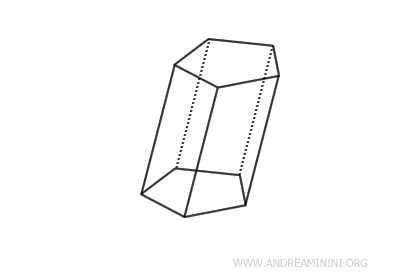
El prisma es una figura sólida fundamental en la geometría espacial.

Características principales de un prisma

Las caras paralelas y congruentes reciben el nombre de bases del prisma. Dichas bases pueden adoptar cualquier forma poligonal.

Cada lado de las bases se llama arista de la base.

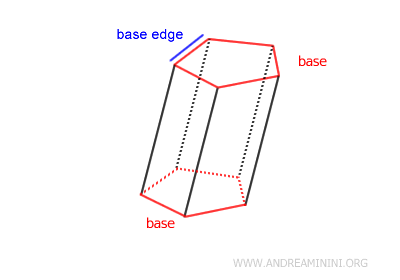
La forma de las bases determina el nombre del prisma. Por ejemplo, un prisma cuyas bases son triángulos se denomina prisma triangular. Si las bases son cuadriláteros, se trata de un prisma cuadrangular; con cinco lados, es un prisma pentagonal; con seis, un prisma hexagonal, y así sucesivamente. Cuando las bases son polígonos regulares, el prisma se llama prisma regular. De lo contrario, se clasifica como “irregular”.

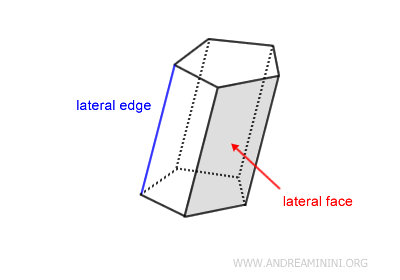
Las otras caras, conocidas como caras laterales, son paralelogramos que unen los vértices correspondientes de las dos bases.

El segmento que une dos vértices situados en distintas bases se llama arista lateral.

En un prisma, todas las aristas laterales son congruentes.

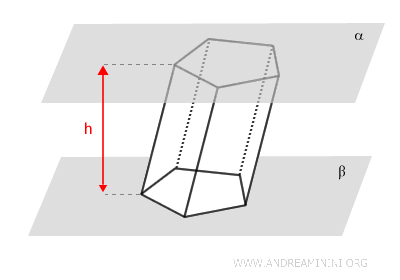
La distancia entre las dos bases se denomina altura del prisma.

Las diagonales del prisma son los segmentos que unen vértices que no se encuentran en la misma base.

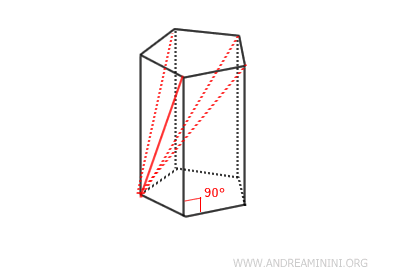
Tipos de prismas

Los prismas se pueden clasificar en función de la forma de sus bases:

• Prisma triangular
  Posee bases triangulares.
• Prisma cuadrangular
  Posee bases cuadriláteras.
• Prisma pentagonal
  Posee bases pentagonales.
  
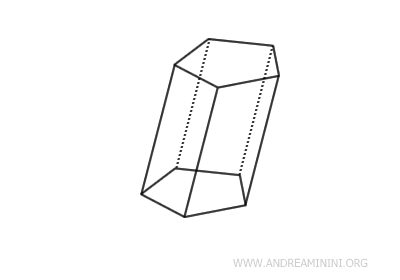
• Paralelepípedo
  Un paralelepípedo es un prisma cuyas bases son paralelogramos.
  

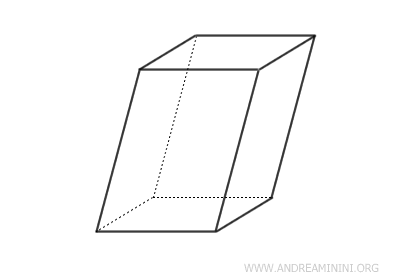
Y así sucesivamente, para cualquier otra base poligonal.

Además, los prismas se pueden clasificar según la disposición de sus caras laterales:

• Prisma recto
  Sus caras laterales son rectángulos, y el ángulo entre la base y las caras laterales es de 90 grados. En un prisma recto, las aristas laterales (es decir, los segmentos que unen vértices correspondientes de las dos bases) son perpendiculares a los planos de las bases. Esto implica que dichas aristas laterales coinciden con la altura del prisma.
  
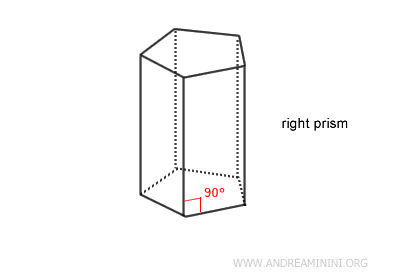
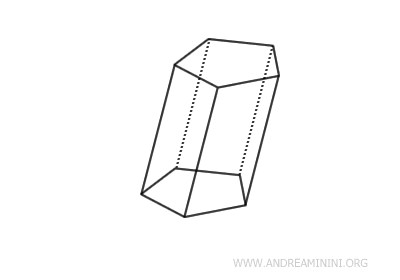
• Prisma oblicuo
  Sus caras laterales también son paralelogramos, pero no rectángulos.
  
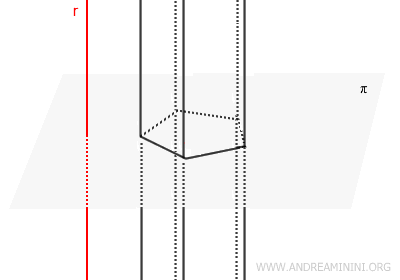
• Prisma ilimitado
  Un prisma ilimitado es una figura geométrica generada a partir de un polígono y de un conjunto de rectas que son todas paralelas a una recta dada \( r \), la cual no pertenece al plano del polígono. Esta figura se extiende indefinidamente en ambas direcciones a lo largo de esas rectas paralelas, formando un sólido tridimensional infinito.
  
• Prisma limitado
  Un prisma limitado, conocido habitualmente simplemente como prisma, es un poliedro que se obtiene al seccionar un prisma ilimitado mediante dos planos paralelos. Está compuesto por dos bases poligonales congruentes y por caras laterales que son paralelogramos.
  

Volumen y área superficial de un prisma

El volumen de un prisma se calcula multiplicando el área de su base A por la altura h del prisma: $$ V = A \cdot h $$

El área superficial total S de un prisma es la suma de las áreas de sus dos bases más las áreas de sus caras laterales.

Si P es el perímetro de la base y h es la altura del prisma, el área lateral es P h. Por lo tanto, el área superficial total se expresa así:

$$ S = 2A + P \cdot h $$

Prisma recto

Un prisma recto es un tipo de prisma en el que las aristas laterales son perpendiculares a las bases.

En un prisma recto, las caras laterales son rectángulos y la altura del prisma coincide con la longitud de las aristas laterales.

Notas

Observaciones adicionales, teoremas y reflexiones sobre la geometría de los prismas.

• Teorema de equivalencia de prismas
  Dos prismas tienen el mismo volumen si sus bases poseen igual área y sus alturas son congruentes.

  Demostración. Consideremos dos prismas - no necesariamente congruentes - situados sobre un mismo plano $ \pi $. Según la hipótesis, ambos sólidos tienen bases con la misma área, $ \text{Área}(ABC) = \text{Área}(ABCD) $, y la misma altura $ AH $.
  
  Sea $ \pi' $ un plano cualquiera paralelo a la base que interseque ambos prismas. Las secciones planas obtenidas - $A'B'C'$ y $A'B'C'D'$ - son congruentes a sus respectivas bases. Esto se deduce de la definición misma de prisma, donde los vértices correspondientes están unidos mediante segmentos paralelos e iguales en longitud a la altura.
  
  Como todo plano $ \pi' $ paralelo a la base genera secciones de igual área, según el Principio de Cavalieri, ambos sólidos deben tener el mismo volumen. Por lo tanto, los dos prismas son sólidos equivalentes en volumen.

• Si dos prismas tienen bases congruentes, sus volúmenes son proporcionales a sus alturas.

  Demostración. El volumen $V$ de cualquier prisma se obtiene multiplicando el área de su base por su altura, es decir, la distancia perpendicular entre las dos bases: $$ V = A_B \cdot h $$ donde $A_B$ es el área de la base y $h$ es la altura del prisma. Si dos prismas tienen bases congruentes (es decir, con la misma área $A_B$) y el mismo volumen, entonces deben tener también la misma altura: $$ V_1 = V_2 \quad \text{y} \quad A_{B_1} = A_{B_2} \quad \Rightarrow \quad h_1 = h_2 $$ Por el contrario, si los dos prismas tienen igual área de base pero volúmenes distintos, entonces sus volúmenes son directamente proporcionales a sus alturas: $$ \frac{V_1}{V_2} = \frac{A_B \cdot h_1}{A_B \cdot h_2} = \frac{h_1}{h_2} $$ En resumen, cuando la base es fija, el volumen de un prisma varía de forma lineal con su altura.

Y así sucesivamente.