Cono

Un cono es un sólido generado al hacer girar un triángulo rectángulo ABC alrededor de uno de sus catetos, que actúa como eje de rotación.

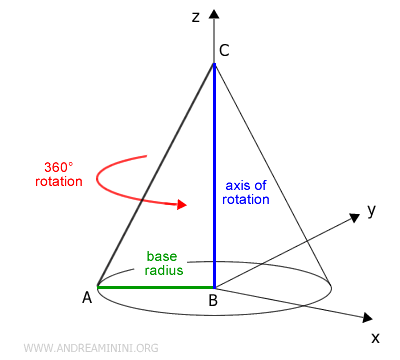
El cateto elegido como eje determina la altura del cono.

El otro cateto define el radio de la base, mientras que la hipotenusa recibe el nombre de generatriz o altura inclinada.

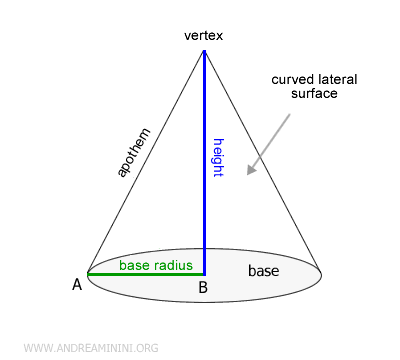
El cono está formado por una base circular y una superficie lateral curva que converge en un punto denominado vértice.

El vértice es el punto donde se encuentran todas las generatrices, opuesto a la base.

El cono es uno de los sólidos de revolución más representativos, junto con la esfera y el cilindro.

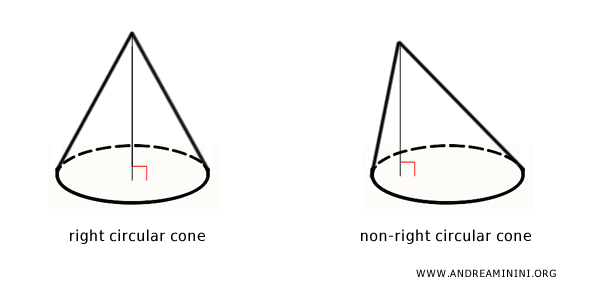
En geometría elemental, el término “cono” suele referirse al cono circular recto, es decir, aquel cuya base es un círculo y cuya altura es perpendicular a dicha base. No obstante, existen otras variantes conocidas como conos indefinidos, entre las que se encuentran el cono elíptico, el cono circular oblicuo, el cono cuadrático, entre otros. El cono circular recto es simplemente una de las muchas formas posibles. Algunos conos no pueden generarse mediante la rotación de un triángulo, como ocurre con el cono oblicuo, en el cual la altura no coincide con el eje de simetría.

Fórmulas

A continuación se presentan las fórmulas fundamentales para calcular las propiedades de un cono circular recto:

El área lateral se obtiene multiplicando la longitud de la circunferencia de la base (πr) por la generatriz del cono:

$$ S_L = \pi r \cdot a $$

donde \( r \) es el radio de la base y \( a \) es la generatriz (o apotema).

Área de la base

Como la base es un círculo, su área se calcula mediante:

$$ S_B = \pi r^2 $$

Área total

El área total del cono es la suma del área lateral y el área de la base:

$$ S_T = S_L + S_B $$

$$ S_T = \pi r a + \pi r^2 $$

$$ S_T = \pi r (a + r) $$

Volumen del cono

El volumen de un cono equivale a un tercio del volumen de un cilindro que tenga la misma base y altura:

$$ V = \frac{1}{3} \pi r^2 h $$

Nota. De acuerdo con el teorema de equivalencia de volúmenes entre conos y pirámides, la fórmula general es:
$$ V = \frac{1}{3} A h = \frac{1}{3} \pi r^2 h $$

Tipos de conos

Los conos pueden clasificarse según las características geométricas de su base y la posición de su eje. A continuación se enumeran los principales:

• Cono circular recto
  Es el tipo más habitual. Tiene base circular y altura perpendicular a la base. El eje del cono coincide con la altura y atraviesa el centro de la base.
• Cono circular oblicuo
  Tiene base circular, pero el eje está inclinado respecto al plano de la base. El vértice no se encuentra alineado con su centro.
• Cono elíptico
  La base es una elipse. El eje puede ser perpendicular u oblicuo respecto al plano base, generando superficies de distinta inclinación.
• Cono parabólico
  Se obtiene al girar una parábola alrededor de su eje de simetría. A diferencia de los conos circulares, no posee una base cerrada definida.
• Cono hiperbólico
  Se forma al girar una hipérbola en torno a su eje. La superficie resultante está compuesta por dos hojas simétricas que se abren en sentidos opuestos.
• Cono esférico
  Se genera al girar una semicircunferencia alrededor de su diámetro. Aunque su forma se asemeja a la de un casquete esférico, conserva propiedades del cono circular.

Estos son solo algunos ejemplos de los distintos tipos de conos que pueden estudiarse en geometría.

El cono en la geometría analítica

En geometría analítica, el cono es una superficie cuádrica que puede describirse mediante ecuaciones en coordenadas cartesianas tridimensionales.

Ecuación general de un cono

La siguiente ecuación representa distintos tipos de conos - no necesariamente circulares - dependiendo de los valores de \( a \), \( b \) y \( c \):

$$ \left( \frac{x}{a} \right)^2 + \left( \frac{y}{b} \right)^2 - \left( \frac{z}{c} \right)^2 = 0 $$

Si \( x \), \( y \) y \( z \) son las coordenadas de un punto en el espacio, esta ecuación define una superficie cónica con vértice en el origen.

Ecuación del cono circular recto

Una de las formas más comunes del cono en geometría analítica es el cono circular recto, cuya ecuación estándar es:

$$ x^2 + y^2 = z^2 \cdot \left( \frac{r}{h} \right)^2 $$

donde \( r \) es el radio de la base y \( h \) la altura del cono. La razón \( r/h \) determina la inclinación de la superficie lateral.

Esta ecuación describe un cono con vértice en el origen \( (0, 0, 0) \), eje de simetría alineado con el eje \( z \), y base circular ubicada en el plano \( xy \).

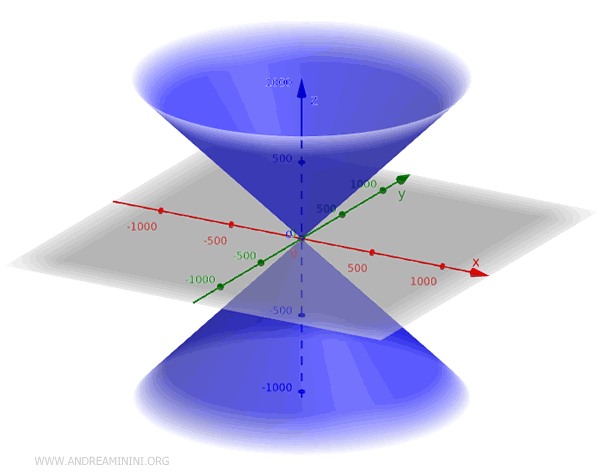
De forma general, esta ecuación representa un cono doble: dos superficies simétricas respecto al plano \( xy \) que se extienden indefinidamente en ambas direcciones del eje \( z \).

Para restringir la figura a una sola de estas mitades, basta con imponer una condición adicional sobre \( z \), por ejemplo \( z > 0 \).

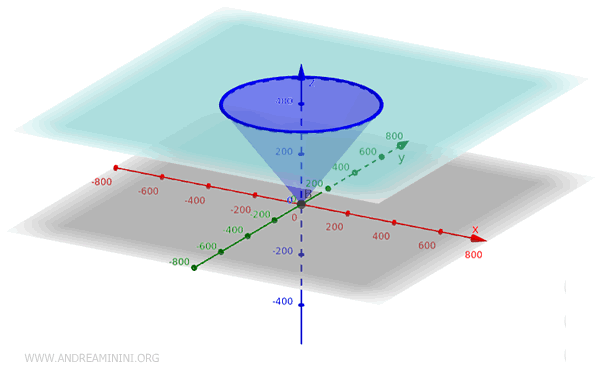
Nota: Las ecuaciones de un cono varían según su orientación y la posición de su vértice. Modificando la forma estándar es posible obtener conos cuyo eje esté alineado con los ejes \( x \) o \( y \), o cuyo vértice se sitúe fuera del origen.

Superficie cónica circular recta

La ecuación de una superficie cónica con vértice en el origen, eje alineado con el eje \( z \) y semiángulo \( \delta \), es:

$$ x^2 + y^2 - k^2 z^2 = 0 $$

donde \( k^2 = \tan^2 \delta \).

Si el eje de la superficie se alinea con el eje \( x \), la ecuación se transforma en:

$$ y^2 + z^2 - k^2 x^2 = 0 $$

Y si el eje es paralelo al eje \( y \):

$$ x^2 + z^2 - k^2 y^2 = 0 $$

En todos los casos, \( k^2 = \tan^2 \delta \).

Demostración

Consideremos una recta \( r \) que pasa por el origen \( O \) y forma un ángulo \( \delta \) con el eje \( y \).

Dicha recta se denomina generatriz del cono, ya que al girar alrededor del eje \( y \) describe toda la superficie cónica.

Sea \( P(x, y, z) \) un punto sobre \( r \), y \( H \) su proyección ortogonal sobre el eje \( y \).

En el triángulo rectángulo \( OPH \), el ángulo en \( O \) es \( \delta \). Por definición trigonométrica:

$$ OH = |OP| \cdot \cos \delta \qquad PH = |OP| \cdot \sin \delta $$

Si consideramos \( |OP| = 1 \), obtenemos:

$$ OH = \cos \delta \qquad PH = \sin \delta $$

Por tanto:

$$ \tan \delta = \frac{PH}{OH} = \frac{\sin \delta}{\cos \delta} $$

Dado que \( OH = |y| \), se sigue que:

$$ \tan \delta = \frac{PH}{|y|} $$

El segmento \( PH \) es el radio de un círculo proyectado sobre el plano \( xz \), cuya ecuación es:

$$ x^2 + z^2 = PH^2 $$

Y como \( PH = \sqrt{x^2 + z^2} \), sustituyendo obtenemos:

$$ \tan \delta = \frac{\sqrt{x^2 + z^2}}{|y|} $$

Elevando al cuadrado ambos miembros:

$$ \tan^2 \delta = \frac{x^2 + z^2}{y^2} $$

Reordenando:

$$ x^2 + z^2 - y^2 \tan^2 \delta = 0 $$

Al definir \( k^2 = \tan^2 \delta \), la ecuación queda:

$$ x^2 + z^2 - k^2 y^2 = 0 $$

Esta es la ecuación de una superficie cónica circular recta con eje paralelo al eje \( y \).

Notas complementarias

Algunas propiedades adicionales sobre los conos:

• Cono equilátero
  Un cono es equilátero cuando su generatriz \( a \) es igual al diámetro de la base: $$ a = 2r $$
  En este caso, la sección que pasa por el eje forma un triángulo equilátero.
• Tronco de cono
  Se obtiene al cortar un cono mediante un plano paralelo a su base y eliminar la parte superior. El sólido resultante tiene dos bases circulares de distinto radio.
• Secciones cónicas
  Las distintas intersecciones entre un cono y un plano generan curvas conocidas como secciones cónicas: elipse, parábola o hipérbola, dependiendo de la inclinación del plano de corte.

Y así sucesivamente…