Pirámide Regular

Una pirámide regular es una pirámide recta cuya base es un polígono regular, es decir, con todos sus lados y ángulos iguales.

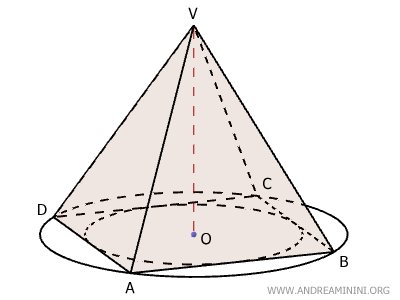
En otras palabras, la base puede ser un triángulo equilátero, un cuadrado, un pentágono regular o cualquier otro polígono regular.

Las pirámides regulares presentan las siguientes características:

• Base regular. La base es siempre un polígono regular, lo que significa que puede tanto inscribirse en una circunferencia como circunscribirse alrededor de ella.
• Caras laterales congruentes. Todas las caras laterales son triángulos isósceles exactamente iguales.
• Altura. Al tratarse de una pirámide recta, su altura (OV) es perpendicular al plano de la base y parte del centro O, que coincide con el centro tanto de la circunferencia inscrita como de la circunscrita.
• Apotema. Cada cara lateral posee una altura propia denominada apotema, que es la distancia perpendicular que va desde el vértice de la pirámide hasta el punto medio de un lado de la base. En una pirámide regular, todas las apotemas son congruentes.

La pirámide regular es una de las figuras geométricas más admiradas, tanto por su simetría perfecta como por la elegancia y solidez que representa en distintas construcciones a lo largo de la historia.

Nota. Las pirámides regulares han sido ampliamente utilizadas en arquitectura e ingeniería. El ejemplo más célebre es la Gran Pirámide de Keops en Egipto, cuyo diseño se basa en proporciones casi perfectamente regulares.

Ejemplo de Pirámide Regular

Veamos el caso de una pirámide con base cuadrada (ABCD), lo que la convierte en una pirámide regular de base cuadrangular.

El vértice V se encuentra exactamente sobre el centro O de la base. El segmento OV es la altura de la pirámide y es perpendicular al plano de la base ABCD.

Las cuatro caras laterales son triángulos isósceles congruentes:

$$ ABV \cong ADB \cong BCV \cong CDV $$

La altura de cada cara lateral se denomina apotema y es idéntica en todas ellas. Por ejemplo, $ EV \cong FV $.

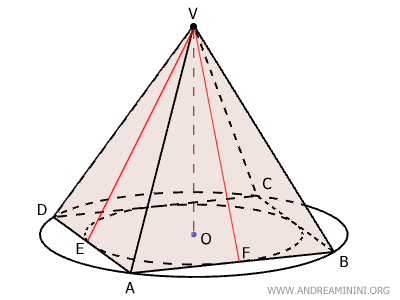
Gracias a su simetría, la base de la pirámide puede tanto inscribirse como circunscribirse en una circunferencia.

Demostración

En una pirámide regular, la base es siempre un polígono regular.

Cualquier polígono regular puede inscribirse y circunscribirse en una circunferencia.

Fijémonos en los puntos de tangencia (E y F) donde la circunferencia inscrita toca los lados del polígono.

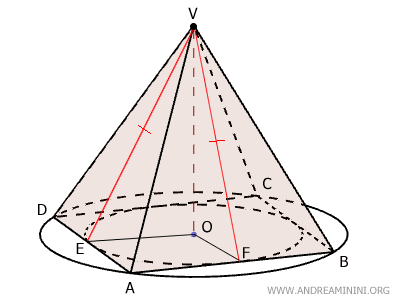
Los segmentos EV y FV representan las apotemas de las caras laterales ADV y ABV de la pirámide recta (véase demostración). Estas apotemas son las alturas de dichos triángulos y forman un ángulo de 90° con los lados de la base AD y AB.

Los segmentos OE y OF son congruentes, ya que son radios de la misma circunferencia.

$$ OE \cong OF $$

Los ángulos $ E \hat{O} V \cong F \hat{O} V $ miden ambos 90°, porque $ OV $, la altura de la pirámide, es perpendicular al plano de la base ABCD.

$$ E \hat{O} V \cong F \hat{O} V = 90° $$

Según el primer criterio de congruencia de triángulos, los triángulos OEV y OFV son congruentes, puesto que comparten dos lados iguales y el ángulo recto comprendido.

De ello se deduce que $ EV \cong FV $, lo que confirma que todas las apotemas de la pirámide son congruentes.

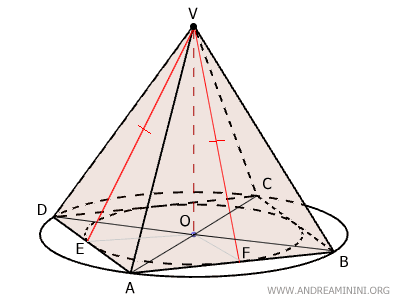
Dado que este razonamiento es válido para todas las caras laterales, se concluye que, en una pirámide regular, todas las apotemas son congruentes.

Consideremos ahora los segmentos $ OA \cong OB \cong OC \cong OD $, que son congruentes al ser radios de la circunferencia circunscrita.

Los triángulos $ OAV \cong OBV \cong OCV \cong ODV $ son congruentes, ya que poseen dos lados congruentes y un ángulo recto en común.

En consecuencia, los segmentos $ AV \cong BV \cong CV \cong DV $ también son congruentes.

Esto implica que los triángulos $ ABV $ y $ ADV $ son triángulos isósceles, pues tienen dos lados iguales.

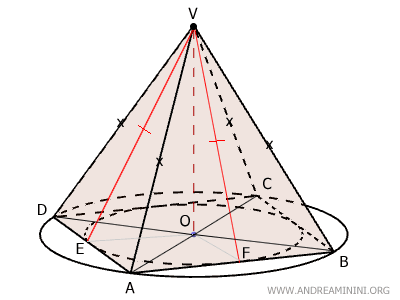
Además, la altura (apotema) de estos triángulos isósceles actúa también como mediana, por lo que los puntos E y F son los puntos medios de los lados AD y AB, respectivamente.

$$ AE \cong ED \cong AF \cong BF $$

Por el tercer criterio de congruencia de triángulos, los triángulos $ ABV \cong ADV $ son congruentes, ya que sus lados correspondientes son congruentes.

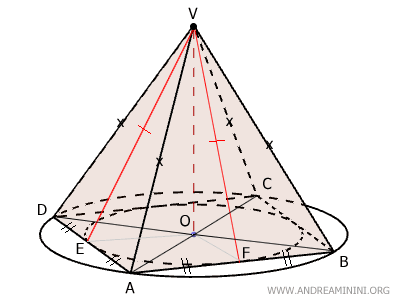
Este razonamiento es válido para cada cara lateral, por lo que se concluye que todas las caras laterales de una pirámide regular son triángulos isósceles congruentes.

Fórmulas Fundamentales

A continuación se presentan algunas fórmulas clave para calcular las principales propiedades de una pirámide regular.

• Área de la Base
  El área de la base depende tanto del número de lados como de la longitud de cada lado. Se determina mediante la fórmula: \[ A_b = \frac{n \cdot l^2}{4} \cdot \cot \frac{180^\circ}{n} \] donde \( n \) es el número de lados de la base, \( l \) es la longitud de cada lado, y \( \cot \) es la cotangente del ángulo central asociado al polígono regular. En el caso particular de una base cuadrada, la fórmula se simplifica a **\( A_b = l^2 \)**, ya que el área de un cuadrado se calcula de manera directa.

  Ejemplo. Si la base es un pentágono regular de lado \( l = 5 \) cm, su área es: \[ A_b = \frac{5 \cdot 5^2}{4} \cdot \cot \frac{180^\circ}{5} \approx 43.01 \text{ cm}^2 \]

• Área Lateral
  El área lateral corresponde a la suma de todas las caras triangulares que conforman los lados de la pirámide. Se calcula mediante: \[ A_L = \frac{n \cdot l \cdot a}{2} \] donde \( n \) es el número de lados de la base, \( l \) la longitud del lado, y \( a \) la apotema (la altura inclinada de la pirámide), que coincide con la altura de cada cara triangular isósceles. Cada cara lateral tiene un área de \( \frac{l \cdot a}{2} \). Al multiplicar por \( n \), se obtiene el área lateral total.

  Ejemplo. Si la pirámide tiene una base hexagonal (\( n = 6 \)) con lados de \( 4 \) cm y una apotema de \( 7 \) cm, su área lateral es: \[ A_L = \frac{6 \cdot 4 \cdot 7}{2} = 84 \text{ cm}^2 \]

• Volumen de la Pirámide
  El volumen de una pirámide regular se determina con la fórmula: \[ V = \frac{A_b \cdot h}{3} \] donde \( A_b \) es el área de la base y \( h \) la altura perpendicular de la pirámide (la distancia entre el vértice y el centro de la base). Esta fórmula es análoga a la del volumen de un prisma, con la diferencia de que la pirámide ocupa solo un tercio del volumen del prisma con igual base y altura. Esto se debe a que la pirámide se estrecha hacia su vértice, reduciendo su volumen respecto a un sólido de sección constante.

  Ejemplo. Si una pirámide tiene base cuadrada de lado \( l = 6 \) cm, su área base es \( A_b = 36 \) cm², y su altura es \( 10 \) cm, entonces su volumen será: \[ V = \frac{36 \cdot 10}{3} = 120 \text{ cm}^3 \]

Y así sucesivamente.