Trapecio

Un trapecio es un cuadrilátero que posee exactamente dos lados paralelos.

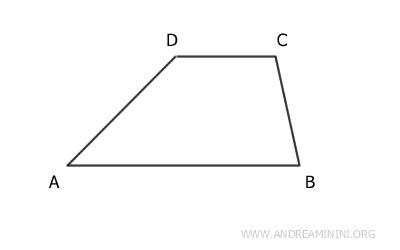
Los lados paralelos reciben el nombre de bases del trapecio.

A diferencia de otros cuadriláteros con lados paralelos, como los rectángulos, en un trapecio las bases no son congruentes, es decir, tienen longitudes distintas.

• Base mayor
  La base mayor es el lado más largo entre los dos lados paralelos.
• Base menor
  La base menor es el lado más corto de los dos lados paralelos.

La distancia perpendicular que separa las dos bases se denomina altura del trapecio.

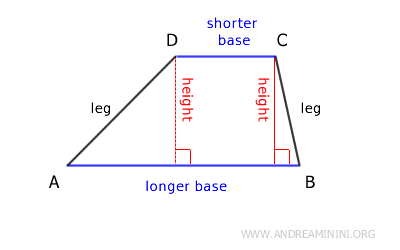
Los otros dos lados, que no son paralelos, se conocen como lados oblicuos.

Una propiedad esencial del trapecio es que los ángulos interiores adyacentes a cada lado oblicuo son suplementarios, es decir, suman 180° (un ángulo llano).

Existen distintos tipos de trapecios, entre ellos el trapecio rectángulo, en el cual uno de los lados oblicuos es perpendicular a las bases; el trapecio escaleno, que tiene lados oblicuos de diferente longitud y ninguno perpendicular a las bases; y el trapecio isósceles, que presenta lados oblicuos congruentes.

Fórmulas del Trapecio

A continuación, se muestran las principales fórmulas para calcular las dimensiones de un trapecio:

• Perímetro
  El perímetro de un trapecio se obtiene sumando las longitudes de sus lados oblicuos y de sus dos bases. $$ P = l_1 + l_2 + b_1 + b_2 $$
• Área del Trapecio
  El área del trapecio se calcula tomando la mitad del producto entre la suma de las bases y la altura. $$ A = \frac{(a+b) \cdot h}{2} $$

Tipos de Trapecios

Se distinguen tres tipos principales de trapecios:

• Trapecio Escaleno
  Es aquel cuyos lados oblicuos tienen longitudes diferentes.
  
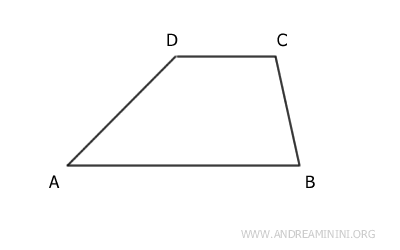
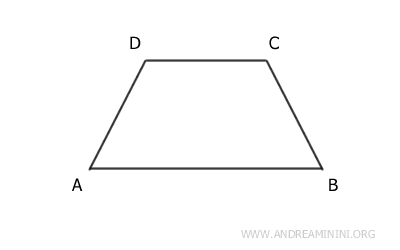
• Trapecio Isósceles
  Es el trapecio que posee lados oblicuos congruentes.
  
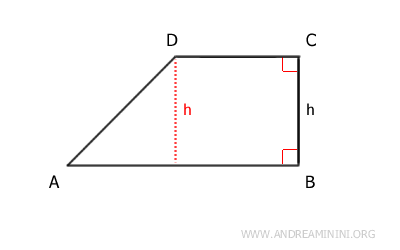
• Trapecio Rectángulo
  Es el trapecio en el que uno de sus lados oblicuos es perpendicular a las bases, formando dos ángulos rectos. En este caso, dicho lado coincide con la altura.
  

El concepto de trapecio tiene raíces en la antigua Grecia, donde matemáticos como Euclides comenzaron a clasificar y estudiar las propiedades de las figuras geométricas. Sin embargo, la diferenciación entre los distintos tipos de trapecios, como el escaleno, se consolidó a medida que la geometría evolucionó a lo largo de los siglos. Por ejemplo, Euclides definía el trapecio simplemente como un cuadrilátero que no es un paralelogramo. Proclo, en cambio, lo definía como un cuadrilátero con dos lados paralelos.

Notas Adicionales

A continuación, algunas observaciones adicionales sobre los trapecios:

• Cada lado oblicuo de un trapecio puede considerarse como una secante que corta dos rectas paralelas
  Esto permite aplicar las propiedades de las rectas paralelas, especialmente el teorema de las rectas paralelas, para determinar los ángulos interiores del trapecio.
  
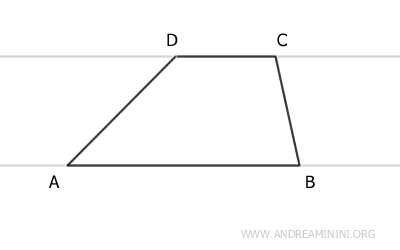
• Los ángulos adyacentes a cada lado oblicuo de un trapecio son suplementarios (180°)
  

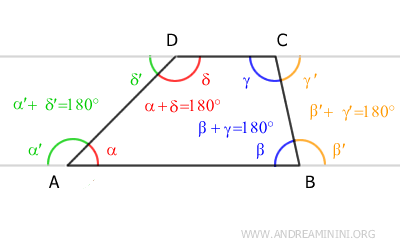
  Demostración: Los ángulos interiores adyacentes a un lado oblicuo de un trapecio pueden considerarse ángulos interiores o exteriores consecutivos formados por una secante que corta dos rectas paralelas. En este caso, las rectas paralelas corresponden a las bases del trapecio (AB y CD), mientras que la secante es la recta que contiene uno de los lados oblicuos (AD o BC). Según el teorema de las rectas paralelas, dichos ángulos son ángulos suplementarios, es decir, suman 180°.

• En un trapecio isósceles, los ángulos adyacentes a cada base son congruentes.
• En un trapecio isósceles, las diagonales también son congruentes.

Y así sucesivamente.