Área del Trapecio
El área de un trapecio se calcula multiplicando la altura (h) por el promedio de las longitudes de sus dos bases, es decir, (b1 + b2) / 2. $$ A = \frac{(b_1+b_2) \cdot h}{2} $$ Aquí, b1 es la base mayor, b2 es la base menor, y h es la altura del trapecio, que corresponde a la distancia perpendicular entre ambas bases.
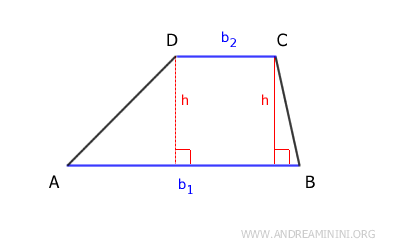
Un trapecio es un cuadrilátero que tiene al menos dos lados paralelos, denominados bases.
El área del trapecio indica la medida de la superficie comprendida en su interior.
Un Ejemplo Práctico
Imaginemos un trapecio cuya base mayor mide 8 cm, la base menor 5 cm y cuya altura es de 4 cm.
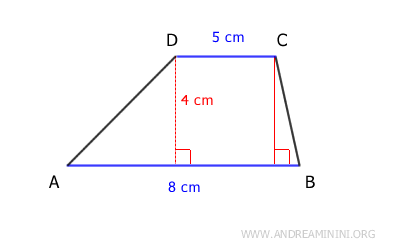
Aplicamos la fórmula:
$$ A = \frac{(8+5) \cdot 4}{2} $$
$$ A = \frac{13 \ \text{cm} \ \cdot 4 \ \text{cm} }{2} $$
$$ A = \frac{52 \ \text{cm}^2 }{2} $$
$$ A = 26 \ \text{cm}^2 $$
Por lo tanto, el área del trapecio en este ejemplo es de 26 cm2.
La Demostración
Si trazamos una línea perpendicular (h) desde los extremos de la base menor hasta la base mayor, el trapecio queda dividido en dos triángulos rectángulos y un rectángulo en la parte central.
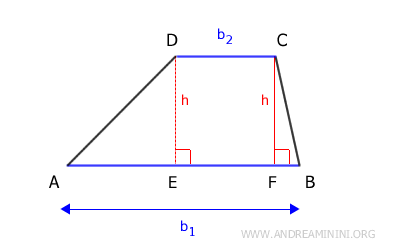
De este modo, el área del trapecio puede entenderse como la suma de las áreas de los dos triángulos (AED y BCF) y la del rectángulo (EFCD).
La suma de las áreas de estas tres figuras es precisamente el área del trapecio (A).
$$ A = \frac{ \overline{AE} \cdot h }{2} + \frac{ \overline{BF} \cdot h }{2} + h \cdot \overline{EF} $$
Aquí, AE·h/2 representa el área del primer triángulo, BF·h/2 la del segundo, y h·EF la del rectángulo.
Extrayendo h como factor común, tenemos:
$$ A = h \cdot \left( \frac{ \ \overline{AE} }{2} + \frac{ \overline{BF} }{2} + \overline{EF} \right) $$
$$ A = h \cdot \left( \frac{ \ \overline{AE} + \overline{BF} + 2 \cdot \overline{EF} }{2} \right) $$
Podemos reescribir 2EF = EF + CD.
$$ A = h \cdot \left( \frac{ \ \overline{AE} + \overline{BF} + \overline{EF} + \overline{CD} }{2} \right) $$
La suma de los segmentos AE + BF + EF = b1 coincide con la longitud de la base mayor.
$$ A = h \cdot \frac{ ( b_1 + \overline{CD} ) }{2} $$
Y dado que el segmento CD = b2 corresponde a la base menor, obtenemos:
$$ A = h \cdot \frac{ ( b_1 + b_2 ) }{2} $$
Este resultado final es exactamente la fórmula que queríamos demostrar.
Otra Demostración
Consideremos el trapecio ABCD.
Prolongamos la base mayor AB añadiendo un segmento en E, de forma que BE sea congruente a CD, la base menor.
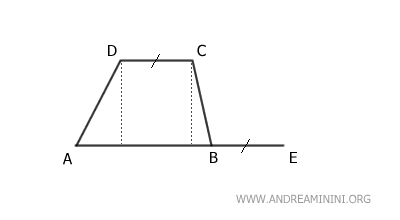
Después, prolongamos la base menor CD añadiendo en el punto D un segmento CF = AB, haciéndolo congruente con la base mayor.
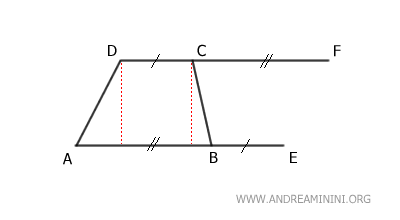
Se traza el segmento EF para unir los puntos E y F.
Con esta construcción, el trapecio se transforma en el paralelogramo ADFE, compuesto por dos trapecios: ABCD y BEFC.
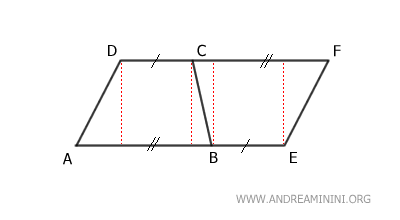
Los trapecios ABCD y BEFC son congruentes, pues poseen los mismos lados en idéntica disposición.
Por lo tanto, el trapecio ABCD equivale a la mitad del paralelogramo ADFE.
El área del paralelogramo se obtiene multiplicando la base por la altura.
$$ A_p = \overline{AE} \cdot h $$
El segmento AE está formado por AB = b1 y BE = b2, que son las bases del trapecio original.
$$ A_p = ( \overline{AB} + \overline{BE} ) \cdot h $$
$$ A_p = ( b_1 + b_2 ) \cdot h $$
Dado que el trapecio representa la mitad del paralelogramo, concluimos que su área es la mitad del área del paralelogramo.
$$ A = \frac{A_p}{2 } $$
$$ A = \frac{ ( b_1 + b_2 ) \cdot h}{2 } $$
De este modo, se demuestra nuevamente la fórmula para calcular el área de un trapecio.
¡Y ahí lo tienes!