Teorema del Trapecio Isósceles
En un trapecio isósceles, los ángulos adyacentes a cada base son congruentes.
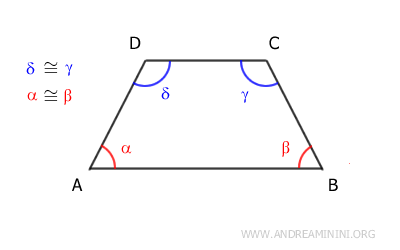
Por ejemplo, en el trapecio isósceles ABCD, los ángulos alfa y beta son congruentes, ya que se encuentran adyacentes a la base mayor AB.
$$ \alpha \cong \beta $$
De manera análoga, los ángulos gamma y delta son congruentes, pues se sitúan adyacentes a la base menor CD.
$$ \gamma \cong \delta $$
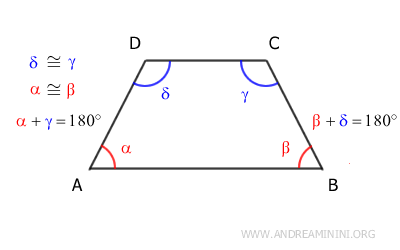
Corolario: En un trapecio isósceles, los ángulos opuestos son suplementarios, es decir, la suma de sus medidas es igual a 180°. $$ \alpha + \gamma = 180° $$ $$ \beta + \delta = 180° $$
Demostración
Consideremos un trapecio isósceles ABDC.
Por definición, en un trapecio isósceles los lados no paralelos son congruentes, AD ≅ CB.
Un trapecio isósceles puede descomponerse en tres figuras geométricas: dos triángulos rectángulos (ADE y BCF) y un cuadrilátero central, que puede ser un rectángulo o un cuadrado (BCDE).
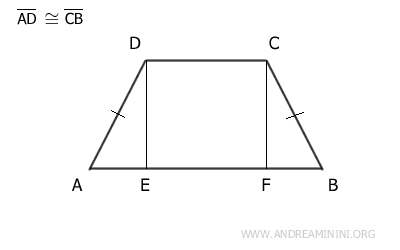
El cuadrilátero BCDE, por definición, posee cuatro ángulos rectos, ya sea que se trate de un rectángulo o de un cuadrado.
Además, los lados DE y CF de este cuadrilátero son opuestos y, por tanto, congruentes, DE ≅ CF.
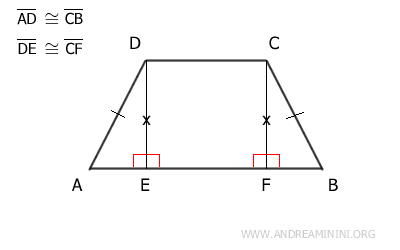
Según el criterio de congruencia de triángulos rectángulos, los triángulos ADE y BCF son congruentes (ADE ≅ BCF), puesto que tienen hipotenusas congruentes (AD ≅ CB) y catetos congruentes (DE ≅ CF).
Como consecuencia, al ser congruentes los triángulos ADE y BCF, sus ángulos correspondientes también lo son.
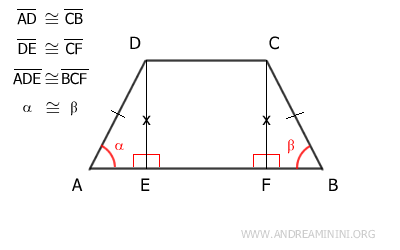
En particular, es fundamental destacar que los ángulos α ≅ β son congruentes.
$$ \alpha = \beta $$
A continuación, aplicamos el teorema de las rectas paralelas, considerando el lado AD como secante que corta a las rectas paralelas AB y CD.
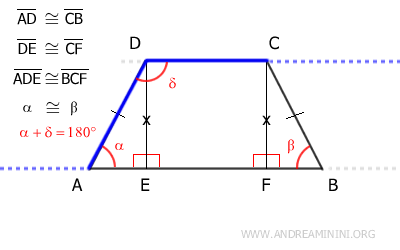
Según este teorema, los ángulos correspondientes (alfa y delta) son suplementarios, es decir, suman 180°.
$$ \alpha + \delta = 180° $$
Del mismo modo, si consideramos el lado BC como secante de las rectas AB y CD, obtenemos un resultado equivalente.
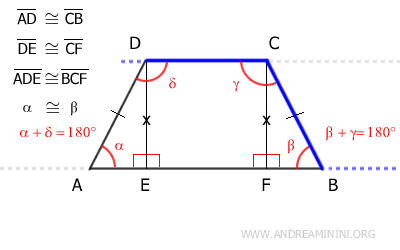
Por la misma razón, los ángulos beta y gamma son suplementarios, β + γ = 180°.
$$ \beta + \gamma = 180° $$
Dado que sabemos que α ≅ β, se deduce que γ ≅ δ, ya que son ángulos suplementarios de ángulos congruentes.
$$ \alpha + \delta \cong \beta + \gamma = 180° $$
$$ \alpha + \delta \cong \beta + \gamma $$
$$ \alpha + \delta - \beta \cong \gamma $$
$$ \delta \cong \gamma $$
En conclusión, los ángulos adyacentes a cada base son congruentes en un trapecio isósceles.
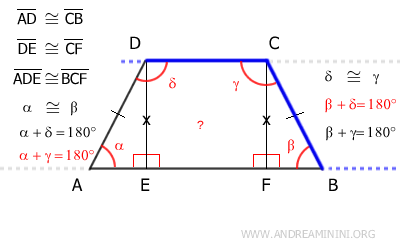
Por lo tanto, dado que los ángulos adyacentes a los lados no paralelos son suplementarios (180°), podemos concluir que en un trapecio isósceles, los ángulos opuestos son suplementarios (α + γ = 180° y β + δ = 180°).
Recíproco del Teorema del Trapecio Isósceles
Si en un trapecio los ángulos adyacentes a una de sus bases son congruentes, entonces se trata de un trapecio isósceles.
Demostración
Como hipótesis inicial, consideremos un trapecio ABCD cuyos ángulos adyacentes a una de sus bases son congruentes.
Por ejemplo, los ángulos α ≅ β adyacentes a la base AB son congruentes.
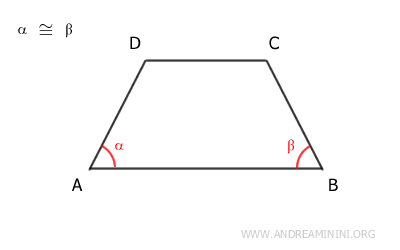
Aunque aún no sabemos de qué tipo de trapecio se trata, sí sabemos que sus bases son paralelas, AB || CD.
En consecuencia, las alturas del trapecio DE y CF son congruentes, DE ≅ CF, y son perpendiculares a las bases, formando ángulos rectos (90°) con la base AB.
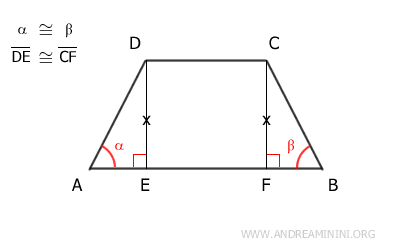
Estas alturas dividen el trapecio en dos triángulos rectángulos: ADE y BCF.
Los triángulos ADE y BCF son congruentes según el segundo criterio de congruencia de triángulos, ya que comparten un lado congruente DE ≅ CF, poseen dos ángulos congruentes α ≅ β y un ángulo recto (90°).
Por lo tanto, los triángulos congruentes ADE ≅ BCF tienen lados y ángulos correspondientes congruentes.
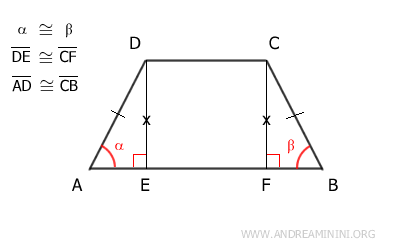
En este contexto, es especialmente relevante señalar que las hipotenusas AD ≅ BC son congruentes, ya que corresponden a los lados no paralelos del trapecio.
En conclusión, dado que el trapecio presenta lados no paralelos congruentes AD ≅ BC, se trata efectivamente de un trapecio isósceles.
Y así sucesivamente.