Teorema de las líneas paralelas

Por tanto, basta que se verifique una de estas condiciones para afirmar que dos rectas son paralelas. Si se cumple una, automáticamente se cumplen todas las demás.

Este resultado también se conoce como el criterio de paralelismo.

Nota: También es válido el teorema recíproco, es decir, si dos rectas son paralelas, entonces cualquier transversal que las corte genera ángulos alternos (internos o externos) congruentes, ángulos correspondientes congruentes y ángulos conjugados suplementarios. Por tanto, se trata de condiciones necesarias y suficientes para el paralelismo de dos rectas.

Demostración

Sean dos rectas $ r $ y $ s $, y una transversal. Queremos demostrar si son paralelas.

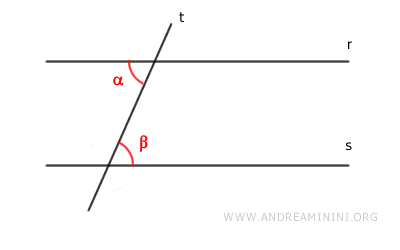
Partimos de la hipótesis de que dos ángulos alternos internos son congruentes:

$$ \alpha \cong \beta $$

Supongamos, por reducción al absurdo, que las dos rectas se cortan en un punto $ C $.

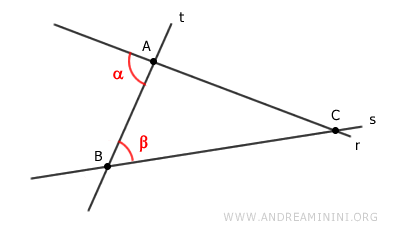
En ese caso, las dos rectas y la transversal formarían el triángulo $ ABC $.

Según el teorema del ángulo exterior, el ángulo exterior $ \alpha $ sería mayor que el ángulo interior no adyacente $ \beta $:

$$ \alpha > \beta $$

Esto contradice la hipótesis inicial $ \alpha \cong \beta $.

Por lo tanto, es falso que dos rectas cortadas por una transversal, con ángulos alternos internos congruentes, se corten en un punto $ C $.

Si no se cortan, entonces son paralelas. Así:
dos rectas $ r $ y $ s $ con ángulos alternos internos congruentes ($ \alpha \cong \beta $) son paralelas.

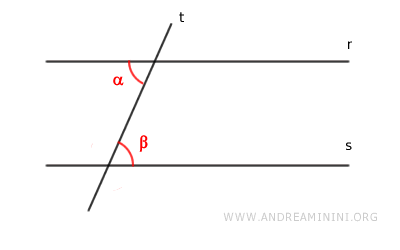
Así queda demostrado el teorema para ángulos alternos internos congruentes.

Los demás casos se reducen a este:

• Ángulos alternos externos congruentes
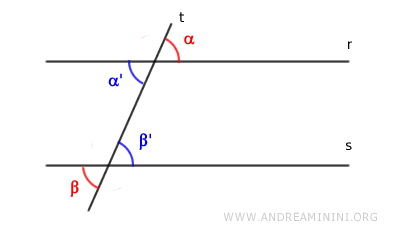
  Si los ángulos alternos externos son congruentes ($ \alpha \cong \beta $), y sabiendo que son opuestos por el vértice a los ángulos alternos internos ($ \alpha' \cong \alpha $, $ \beta' \cong \beta $), se deduce:
  $$ \alpha' \cong \beta' $$
  
• Ángulos correspondientes congruentes
  Si los ángulos correspondientes son congruentes ($ \alpha \cong \beta $), y cada uno es opuesto por el vértice a un ángulo alterno interno ($ \beta \cong \beta' $), entonces:
  $$ \alpha \cong \beta' $$
  
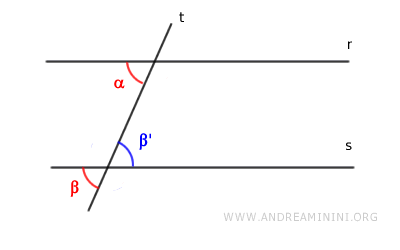
• Ángulos conjugados suplementarios
  Si $ \alpha + \beta = 180° $, y los ángulos adyacentes en $ r $ y $ s $ también suman 180°, se deduce que los alternos internos son congruentes:
  $$ \alpha \cong \beta' $$
  

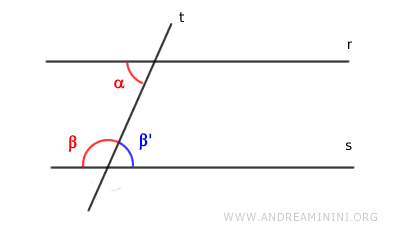
Reducido todo al caso de ángulos alternos internos congruentes, la demostración queda completa.

Teorema recíproco

Demostración

Partimos de la hipótesis:

$$ r // s $$

Queremos demostrar que existen ángulos alternos internos congruentes ($ \alpha \cong \beta $).

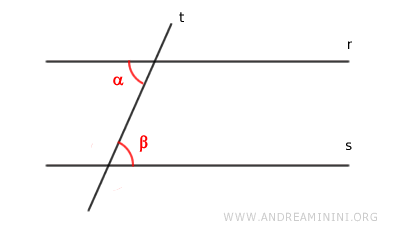
De nuevo, por reducción al absurdo:

Si $ \alpha > \beta $, podríamos trazar otra recta $ r' $ que cumpla $ \alpha' \cong \beta $:

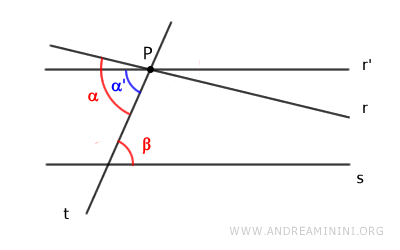
Pero entonces existirían dos rectas paralelas a $ s $ que pasan por $ P $, lo cual contradice el postulado de las paralelas.

Por tanto, las rectas paralelas $ r $ y $ s $ generan necesariamente ángulos alternos internos congruentes.

Del mismo modo, los demás casos se reducen al de ángulos alternos internos congruentes. Por lo tanto, esta demostración es válida para todas las situaciones.

Observaciones

• Corolario

  Si dos rectas $ r $ y $ s $ son perpendiculares a una tercera $ t $, entonces son paralelas entre sí.
  

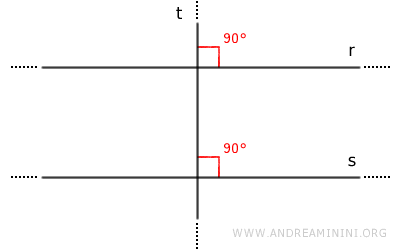
  Nota: En efecto, se generan ángulos correspondientes de 90°, por lo que se cumplen las condiciones del teorema.

• Si una recta es perpendicular a una de dos paralelas, es perpendicular a la otra.

  Demostración:
  $$ r // s $$
  $$ t \perp s $$
  
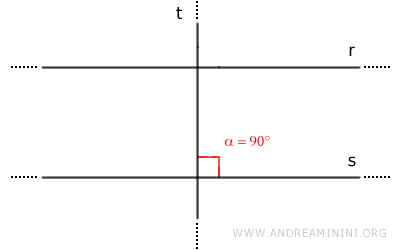
  Por el teorema, $ r $ y $ s $ generan ángulos correspondientes congruentes. Así:
  $$ \beta = 90° $$
  
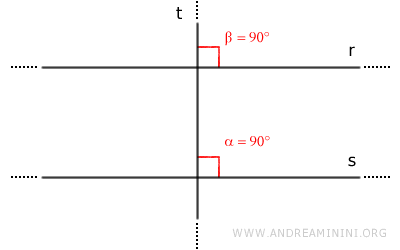
  Entonces $ t \perp r $.

Y así sucesivamente.