Haz de Rectas

¿Qué es un haz de rectas?

Un haz de rectas es un conjunto de rectas en un plano que se define mediante un criterio determinado.

Existen dos tipos de haces de rectas: el haz propio y el haz de rectas paralelas.

Haz de Rectas Paralelas

Un haz de rectas paralelas está formado por todas aquellas rectas que son paralelas a una recta fija r en el plano.

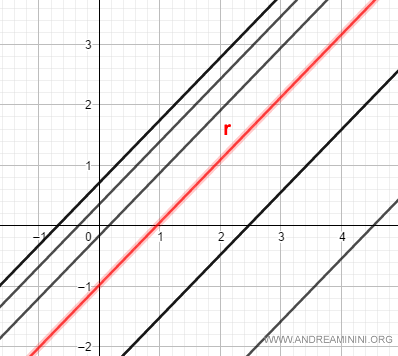
La ecuación cartesiana de un haz impropio de rectas se expresa así:

$$ ax + by + c = 0 $$

donde los coeficientes a y b son distintos de cero.

Cada recta del haz se determina asignando un valor concreto al parámetro c.

Nota: La recta r, respecto a la cual son paralelas las demás, también se identifica mediante un valor específico de c.

Otra forma de expresar la ecuación de un haz de rectas paralelas es la forma explícita:

$$ y = mx + q $$

En esta forma, cada recta del haz se distingue por un valor diferente del término q.

Si q=0, la recta pasa por el origen de coordenadas.

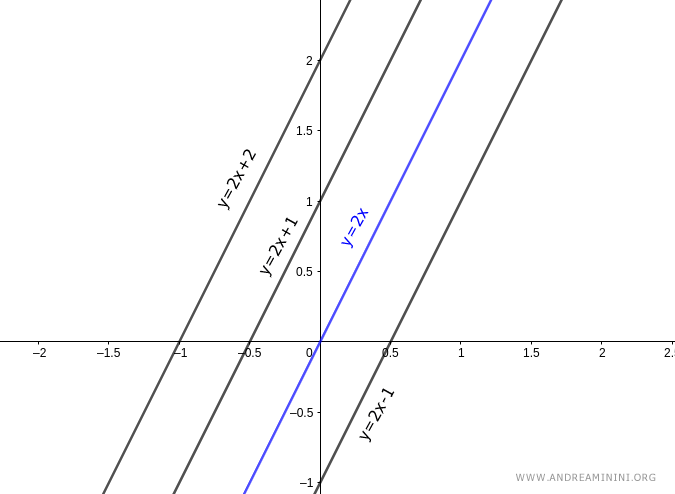
Nota: El término q representa la ordenada en el origen, es decir, el punto en el que la recta corta al eje y cuando x=0.

La ecuación paramétrica del haz de rectas es:

$$ \begin{pmatrix} x \\ y \end{pmatrix} = \begin{pmatrix} x_0 \\ y_0 \end{pmatrix} + t \cdot \begin{pmatrix} l \\ m \end{pmatrix} $$

En este caso, cada recta del haz se obtiene variando el punto (x₀, y₀) por el que pasa.

El vector director (l, m) permanece invariable para todas las rectas del haz.

Ejemplo

La ecuación cartesiana de una recta es:

$$ 2x + 3y - 12 = 0 $$

Si modificamos el parámetro c=12 por otros valores, obtenemos un número infinito de rectas paralelas que forman el haz.

 

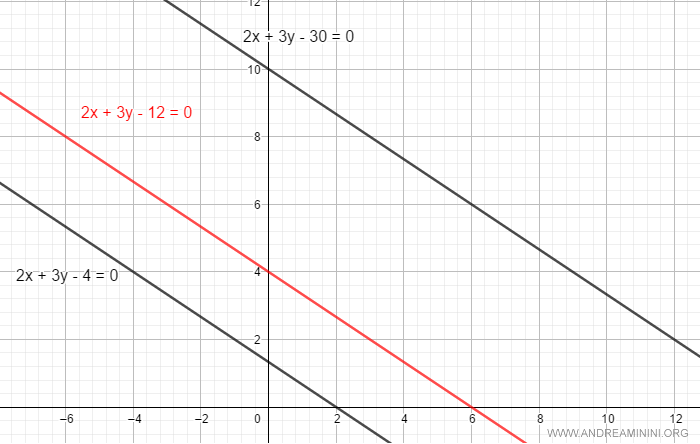
También podemos describir el haz mediante ecuaciones paramétricas:

$$ \begin{pmatrix} x \\ y \end{pmatrix} = \begin{pmatrix} x_0 \\ y_0 \end{pmatrix} + t \cdot \begin{pmatrix} l \\ m \end{pmatrix} $$

$$ \begin{pmatrix} x \\ y \end{pmatrix} = \begin{pmatrix} 0 \\ 4 \end{pmatrix} + t \cdot \begin{pmatrix} 1 \\ -\frac{2}{3} \end{pmatrix} $$

Al variar el punto (0,4), obtenemos las distintas rectas del haz, manteniendo constante el vector director.

El resultado se mantiene coherente.

Haz de Rectas Propio

Un haz de rectas propio está constituido por todas las rectas que pasan por un punto concreto (A) en el plano, llamado centro del haz.

La ecuación de un haz propio con centro en el punto de coordenadas (x₀, y₀) es:

$$ y - y_0 = m \cdot (x - x_0) $$

Al variar la pendiente m ∈ ℝ, se obtienen todas las rectas del haz que pasan por el punto A, salvo la recta paralela al eje y.

Nota: La recta paralela al eje y no puede expresarse mediante la ecuación explícita y = mx, ya que ningún valor de m permite describirla. Para estas rectas se utiliza la ecuación x = x₀. $$ x = x_0 $$

Por tanto, el haz completo de rectas se describe mediante el sistema:

$$ \begin{cases} y - y_0 = m \cdot (x - x_0) \\ \\ x = x_0 \ \ \ \text{si la recta es paralela al eje y} \end{cases} $$

Ejemplo

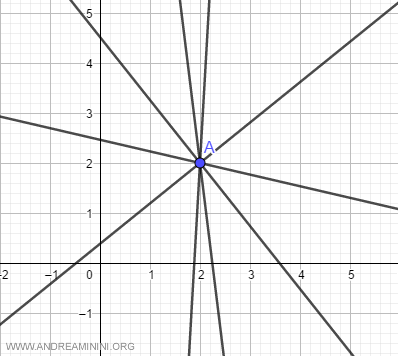
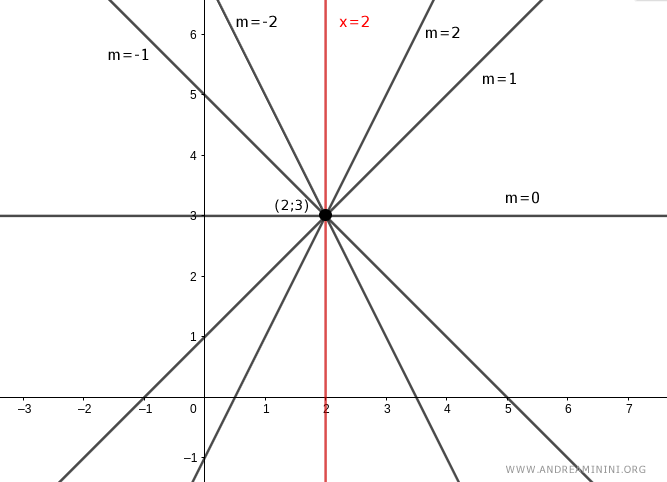
Consideremos el centro del haz C:

$$ C = \begin{pmatrix} x_0 = 2 \\ y_0 = 3 \end{pmatrix} $$

Las ecuaciones correspondientes al haz centrado en C son:

$$ y - y_0 = m \cdot (x - x_0) $$

$$ x = x_0 $$

Con x₀ = 2 e y₀ = 3, las ecuaciones del haz quedan así:

$$ y - 3 = m \cdot (x - 2) $$

$$ x = 2 $$

La primera ecuación, y - 3 = m(x - 2), describe todas las rectas con pendiente variable m, excepto la paralela al eje y.

La segunda ecuación, x = 2, corresponde a la recta paralela al eje y (dibujada en rojo).

Haz de Rectas como Combinación Lineal de Dos Rectas

Un haz de rectas, tanto propio como impropio, también puede generarse mediante la combinación lineal de dos rectas:

$$ r: ax + by + c = 0 $$

$$ s: a'x + b'y + c' = 0 $$

La combinación lineal de ambas rectas es:

$$ p \cdot (ax + by + c) + q \cdot (a'x + b'y + c') = 0 $$

Dividiendo ambos miembros entre p, obtenemos:

$$ ax + by + c + \frac{q}{p} \cdot (a'x + b'y + c') = 0 $$

Definiendo $ k = \frac{q}{p} $, se tiene:

$$ ax + by + c + k \cdot (a'x + b'y + c') = 0 $$

$$ ax + by + c + a'xk + b'yk + c'k = 0 $$

Cada valor de $ k $ determina una recta distinta dentro del haz.

Nota: Esta combinación lineal describe todas las rectas del haz salvo la recta $ s: a'x + b'y + c' = 0 $, ya que ningún valor de $ k $ reproduce exactamente dicha recta. $$ ax + by + c + k \cdot (a'x + b'y + c') = 0 $$

Al agrupar los términos que contienen x e y, se obtiene:

$$ (ax + a'xk) + (by + b'yk) + c + c'k = 0 $$

$$ (a + a'k) \cdot x + (b + b'k) \cdot y + c + c'k = 0 $$

Esta es la ecuación general de un haz de rectas.

Un haz puede clasificarse como propio o impropio:

• Haz de Rectas Propio
  Se da si la razón entre los coeficientes a y b en ambas ecuaciones es distinta $$ \frac{a}{b} \ne \frac{a'}{b'} $$
• Haz de Rectas Impropio
  Ocurre cuando la razón entre los coeficientes a y b en ambas ecuaciones es la misma, lo que significa que las dos rectas son paralelas o coincidentes. $$ \frac{a}{b} = \frac{a'}{b'} $$

Ejemplo

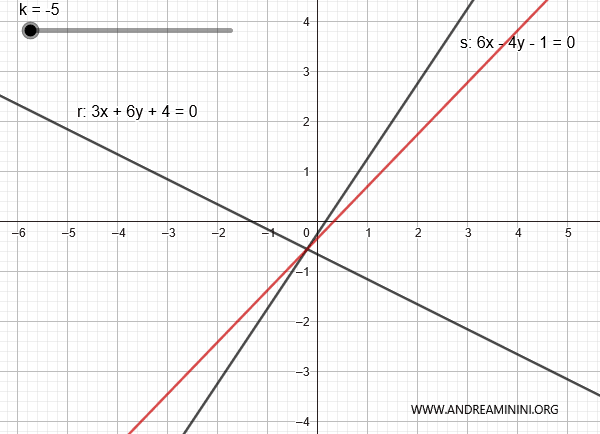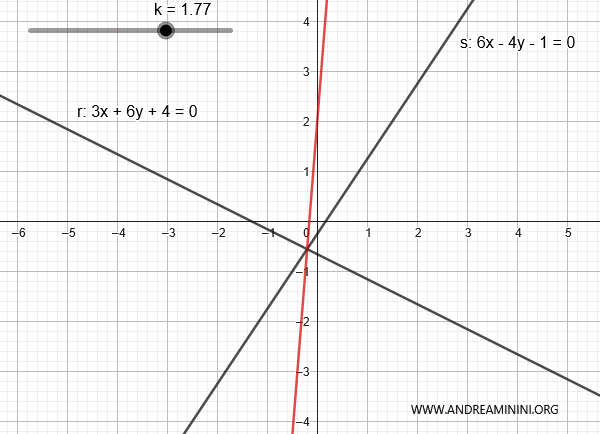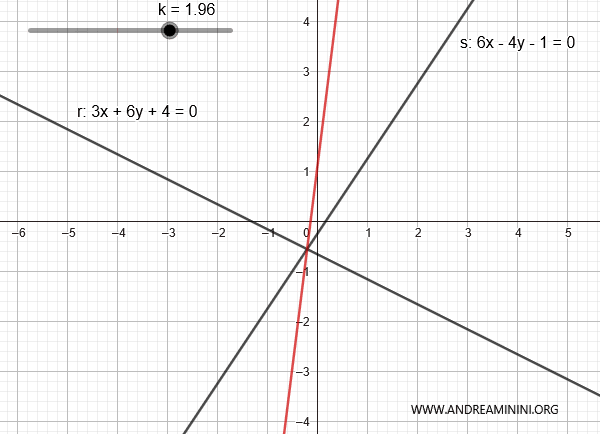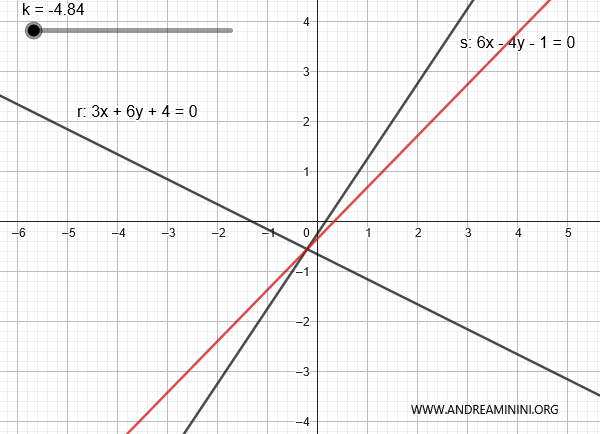
Consideremos las rectas:

$$ r: 3x + 6y + 4 = 0 $$

$$ s: 6x - 4y - 1 = 0 $$

Estas son las dos rectas representadas en el plano:

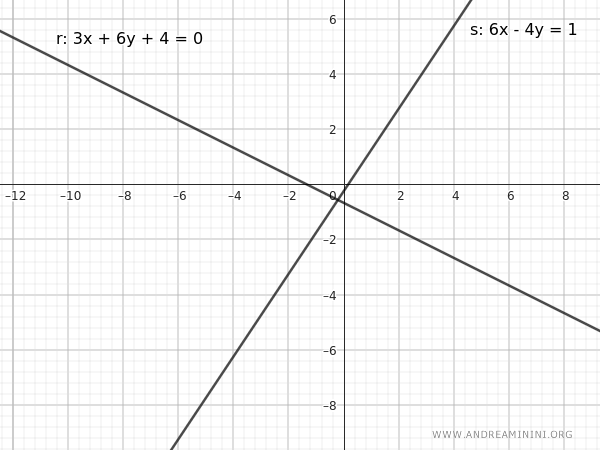
En este caso, se cortan porque las razones entre sus coeficientes son distintas:

$$ \frac{a}{b} \ne \frac{a'}{b'} $$

$$ \frac{3}{6} \ne \frac{6}{4} $$

Por lo tanto, se trata de un haz de rectas propio.

La combinación de ambas rectas es:

$$ 3x + 6y + 4 + k \cdot (6x - 4y - 1) = 0 $$

$$ 3x + 6y + 4 + 6xk - 4yk - k = 0 $$

$$ (3x + 6xk) + (6y - 4yk) + 4 - k = 0 $$

$$ (3 + 6k) \cdot x + (6 - 4k) \cdot y + 4 - k = 0 $$

Al variar k, se pueden generar las demás rectas del haz, salvo la recta s.