Cómo Representar una Recta Mediante un Vector

Un vector geométrico indica una dirección que comparten todas las rectas del plano que son paralelas a él.

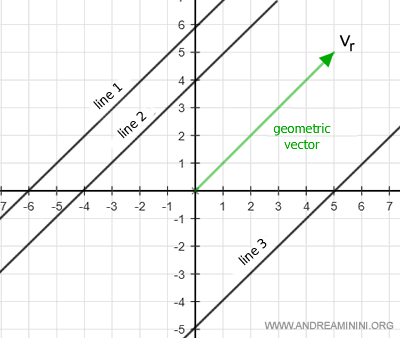
Por lo tanto, cualquier recta en el plano se puede describir mediante:

• un vector geométrico no nulo v_r, llamado vector director, que define la dirección de la recta: $$ v_r = \begin{pmatrix} l \\ m \end{pmatrix} $$

  Los valores l y m se conocen como los parámetros directores de la recta.

• un punto concreto P₀ en el plano por el que pasa la recta: $$ P_0 = \begin{pmatrix} x_0 \\ y_0 \end{pmatrix} $$

  Ejemplo
  

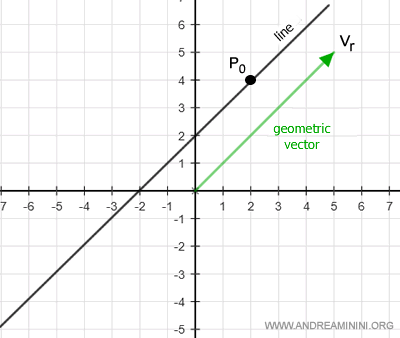
Un punto del plano pertenece a la recta si existe un número real α tal que

$$ OP = OP_0 + α v_r $$

Ejemplo

Consideremos el punto P₁ con coordenadas (-5, -3).

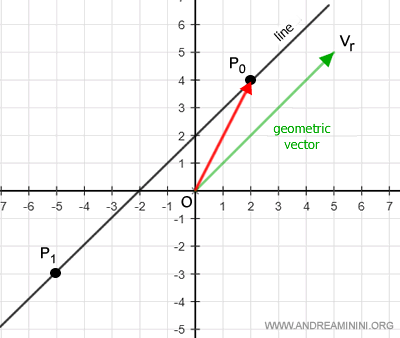
El punto P₁ pertenece a la recta si se cumple que

$$ OP_1 = OP_0 + α v_r $$

$$ \begin{pmatrix} -5 \\ -3 \end{pmatrix} = \begin{pmatrix} 2 \\ 4 \end{pmatrix} + α \begin{pmatrix} 5 \\ 5 \end{pmatrix} $$

Para hallar el valor de α, resolvemos el siguiente sistema de ecuaciones:

$$ \begin{cases} -5 = 2 + 5\alpha \\ -3 = 4 + 5\alpha \end{cases} = \begin{cases} \alpha = - \frac{7}{5} \\ \alpha = - \frac{7}{5} \end{cases} $$

El sistema se resuelve con el valor α = -7/5.

En efecto:

$$ \begin{pmatrix} -5 \\ -3 \end{pmatrix} = \begin{pmatrix} 2 \\ 4 \end{pmatrix} + α \begin{pmatrix} 5 \\ 5 \end{pmatrix} $$

$$ \begin{pmatrix} -5 \\ -3 \end{pmatrix} = \begin{pmatrix} 2 \\ 4 \end{pmatrix} + \begin{pmatrix} 5\alpha \\ 5\alpha \end{pmatrix} $$

$$ \begin{pmatrix} -5 \\ -3 \end{pmatrix} = \begin{pmatrix} 2 \\ 4 \end{pmatrix} + \begin{pmatrix} 5 \cdot \left( - \frac{7}{5} \right) \\ 5 \cdot \left( - \frac{7}{5} \right) \end{pmatrix} $$

$$ \begin{pmatrix} -5 \\ -3 \end{pmatrix} = \begin{pmatrix} 2 \\ 4 \end{pmatrix} + \begin{pmatrix} -7 \\ -7 \end{pmatrix} $$

$$ \begin{pmatrix} -5 \\ -3 \end{pmatrix} = \begin{pmatrix} 2 - 7 \\ 4 - 7 \end{pmatrix} $$

$$ \begin{pmatrix} -5 \\ -3 \end{pmatrix} = \begin{pmatrix} -5 \\ -3 \end{pmatrix} $$

De este modo, podemos generalizar el resultado y afirmar que

Las coordenadas de cualquier punto sobre la recta vienen dadas por la siguiente ecuación, conocida como la ecuación vectorial de la recta: $$ \begin{pmatrix} x \\ y \end{pmatrix} = \begin{pmatrix} x_0 \\ y_0 \end{pmatrix} + \alpha \cdot \begin{pmatrix} l \\ m \end{pmatrix} $$ Si expresamos la ecuación vectorial como un sistema, obtenemos las ecuaciones paramétricas de la recta: $$ \begin{cases} x = x_0 + \alpha \, l \\ y = y_0 + \alpha \, m \end{cases} $$

Existen infinitas ecuaciones vectoriales y paramétricas, ya que podemos multiplicar el vector director por cualquier número distinto de cero.

Ecuaciones Cartesianas

El vector P₀P₁ es paralelo al vector director v_r.

Según la teoría, un vector es paralelo y proporcional a otro si se cumple que

$$ \begin{pmatrix} x - x_0 & l \\ y - y_0 & m \end{pmatrix} \le 1 $$

Esto sucede si

$$ det \begin{pmatrix} x - x_0 & l \\ y - y_0 & m \end{pmatrix} = 0 $$

Al calcular el determinante, se obtiene:

$$ m ( x - x_0 ) - l ( y - y_0 ) = 0 $$

Esta es la ecuación cartesiana de la recta.

Del mismo modo, existen infinitas ecuaciones cartesianas que representan la misma recta.