Vectores geométricos
¿Qué es un vector geométrico?
Un vector geométrico es el conjunto de todos los segmentos dirigidos que son equivalentes entre sí.
En matemáticas, el vector geométrico es una noción abstracta que resume la propiedad común compartida por una familia de segmentos equivalentes.
Segmentos dirigidos equivalentes
Dos segmentos dirigidos, como AB y CD, se consideran equivalentes si tienen la misma dirección, el mismo sentido y la misma longitud (también llamada módulo o magnitud escalar).
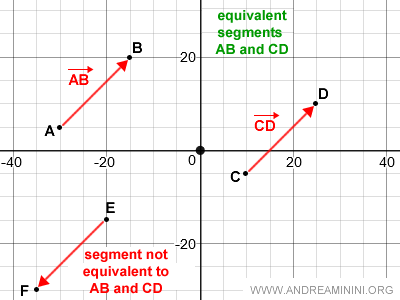
Nota. Los segmentos AB y CD son equivalentes porque coinciden en dirección, sentido y longitud. En cambio, el segmento EF no lo es, ya que, aunque tiene la misma dirección y longitud, su sentido es opuesto.
La relación de equivalencia entre dos segmentos dirigidos se expresa del siguiente modo:
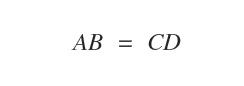
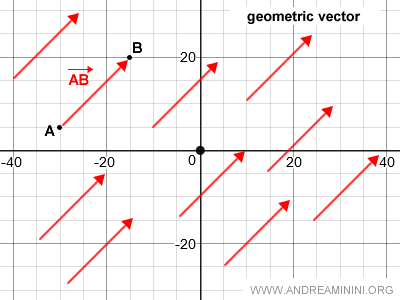
Al trasladar el segmento AB en el plano cartesiano se obtienen infinitos segmentos equivalentes.
El conjunto de todos los segmentos equivalentes a AB, obtenidos mediante traslación, constituye un vector geométrico.
Por tanto, se puede afirmar que:
Dadas una dirección, un sentido y una magnitud, existe un único vector geométrico que posee esas características.
En conclusión, un vector geométrico es un objeto abstracto que representa una clase de segmentos dirigidos equivalentes.
Diferencia entre vectores libres y vectores aplicados
Un vector puede ser libre o aplicado.
- Un vector aplicado está anclado a un punto de origen determinado (O).
- Un vector libre no está vinculado a ningún punto concreto del plano.
Un vector geométrico libre es el conjunto de todos los vectores equivalentes al vector AB (representante de la clase).
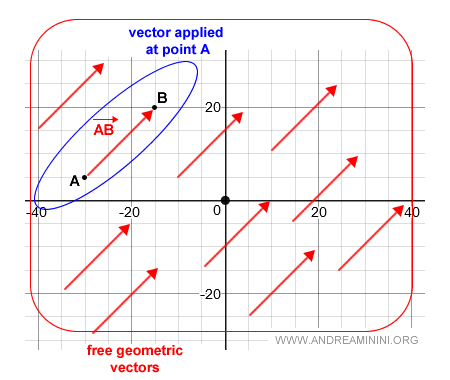
El vector libre representa la clase de equivalencia (o equipolencia) del vector aplicado AB.
Nota. La elección del vector aplicado de referencia - es decir, el representante de la clase - es completamente arbitraria.
El conjunto de todos los vectores libres en un plano forma el llamado conjunto cociente.
Cómo se suman los vectores geométricos
Para sumar dos vectores geométricos libres, se utiliza el método del paralelogramo, colocándolos con un mismo origen (O).
Un ejemplo práctico
En el plano, los vectores geométricos AB y CD pertenecen a clases de equivalencia distintas.
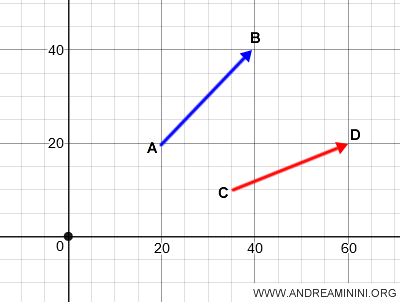
Para sumarlos, reposicionamos ambos vectores de manera que compartan el mismo punto de origen.
Una vez alineados, los vectores AB y CD, con origen común en O, se transforman en OB y OD.
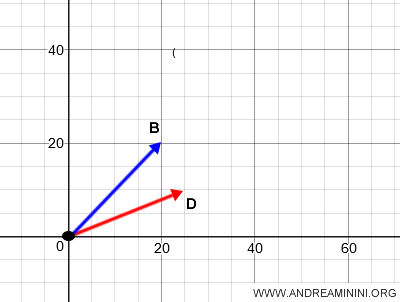
¿Qué origen conviene utilizar? Si el plano ya tiene un origen definido, como el punto O, es preferible usarlo, ya que facilita los cálculos y la representación gráfica.
A continuación, sumamos los vectores OB y OD aplicando el método del paralelogramo.
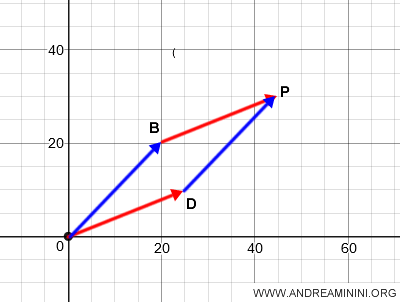
El resultado de la suma de los vectores OB y OD es el vector OP.
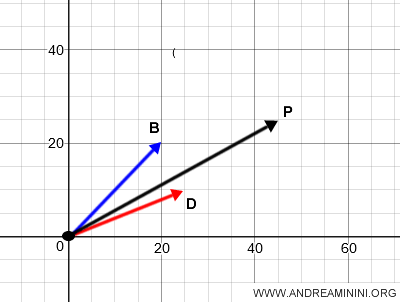
En resumen, el vector OP representa la clase de equivalencia correspondiente a la suma de los vectores geométricos libres AB + CD.
Si se aplica en todos los puntos del plano, el vector OP define el vector geométrico libre resultante.