Ejercicios sobre espacios vectoriales

Aquí te presento algunos ejemplos resueltos sobre espacios vectoriales.

Ejercicio 1

Consideremos los siguientes dos vectores en el espacio vectorial V = R³:

$$ v_1 = \begin{pmatrix} 1 \\ 2 \\ -1 \end{pmatrix} $$

$$ v_2 = \begin{pmatrix} 0 \\ 3 \\ 1 \end{pmatrix} $$

¿Estos dos vectores generan R³?

Para responder a esta pregunta, debemos comprobar si un vector arbitrario v en R³:

$$ v = \begin{pmatrix} a \\ b \\ c \end{pmatrix} \ \in V = R^3 $$

puede escribirse como combinación lineal de v₁ y v₂:

$$ \vec{v} = \lambda_1 \cdot \vec{v}_1 + \lambda_2 \cdot \vec{v}_2 $$

$$ \begin{pmatrix} a \\ b \\ c \end{pmatrix} = \lambda_1 \cdot \begin{pmatrix} 1 \\ 2 \\ -1 \end{pmatrix} + \lambda_2 \cdot \begin{pmatrix} 0 \\ 3 \\ 1 \end{pmatrix} $$

Esto nos conduce a un sistema de tres ecuaciones con dos incógnitas:

$$ \begin{cases} \lambda_1 = a \\ 2 \lambda_1 + 3 \lambda_2 = b \\ - \lambda_1 + \lambda_2 = c \end{cases} $$

Sustituyendo λ₁ = a en las otras dos ecuaciones, obtenemos:

$$ \begin{cases} \lambda_1 = a \\ 2 a + 3 \lambda_2 = b \\ \lambda_2 = c + a \end{cases} $$

Si ahora sustituimos λ₂ = c + a en la segunda ecuación, resulta:

$$ 2 a + 3 (c + a) = b $$

que se simplifica a:

$$ 5 a + 3 c = b $$

Esto muestra que el sistema solo tiene solución si se verifica esta condición. Es decir, no admite soluciones para valores arbitrarios de a, b y c.

Por lo tanto, los dos vectores v₁ y v₂ no generan todo el espacio vectorial V = R³.

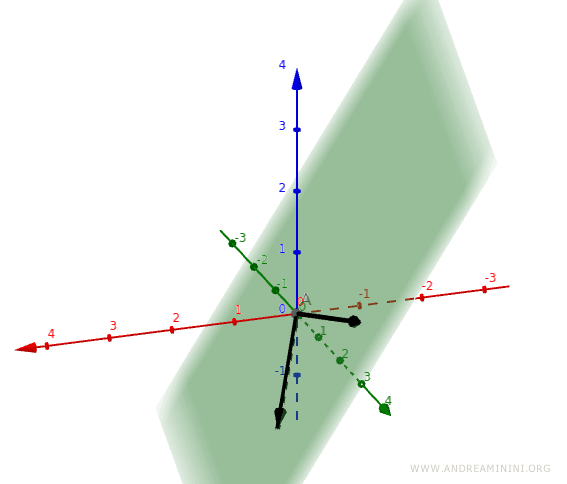
Nota. En general, dos vectores linealmente independientes como mucho generan un plano (R²) en el espacio que ocupan. Dado que V = R³ es un espacio de tres dimensiones, se necesitan al menos tres vectores linealmente independientes para generar todo el espacio.

Ejercicio 2

Consideremos el espacio vectorial M(2,2,R), es decir, el conjunto de todas las matrices reales de 2x2. ¿El subconjunto A de M(2,2,R), formado por matrices de la forma: $$ \begin{pmatrix} a & b \\ c & 1 \end{pmatrix} \ \ \ \ a,b,c \in R $$ es un subespacio vectorial de M(2,2,R)?

Para averiguarlo, comprobaremos si A satisface los axiomas de un espacio vectorial y las condiciones para ser subespacio.

1] ¿El subconjunto A es un espacio vectorial?

El conjunto A no es vacío.

Sin embargo, es inmediato notar que la matriz nula (el elemento neutro respecto a la suma):

$$ \begin{pmatrix} 0 & 0 \\ 0 & 0 \end{pmatrix} \ \ \notin \ A $$

no pertenece a A. La presencia de la matriz nula es un requisito esencial para que un conjunto sea un espacio vectorial.

Por tanto, A no es un espacio vectorial, y en consecuencia, A no es un subespacio de M(2,2,R).

Nota. Este ejemplo pone de manifiesto la utilidad de comprobar primero las condiciones más básicas - como la presencia del elemento neutro - antes de pasar a condiciones más elaboradas. De este modo se ahorra tiempo y esfuerzo.

Ejercicio 3

Consideremos el espacio vectorial M(2,2,R), es decir, el conjunto de todas las matrices reales de 2x2. ¿El subconjunto A de M(2,2,R), formado por matrices de la forma: $$ \begin{pmatrix} a & b \\ c & b-1 \end{pmatrix} \ \ \ \ a,b,c \in R $$ es un subespacio de M(2,2,R)?

Primero verificaremos si A cumple los axiomas de un espacio vectorial.

Después comprobaremos si satisface las condiciones para ser un subespacio.

1] ¿El subconjunto A es un espacio vectorial?

A es claramente un conjunto no vacío.

Sin embargo, es evidente que la matriz nula no pertenece a A:

$$ \begin{pmatrix} 0 & 0 \\ 0 & 0 \end{pmatrix} \ \ \notin \ A $$

Esto se debe a que dos entradas de la matriz dependen del mismo parámetro, concretamente b y b-1:

$$ \begin{pmatrix} a & \color{red}b \\ c & \color{red}{b-1} \end{pmatrix} \ \ \ \ a,b,c \in R $$

Por ejemplo, si elegimos a = 0, b = 0, c = 0, obtenemos:

$$ \begin{pmatrix} 0 & 0 \\ 0 & \color{red}{-1} \end{pmatrix} \ \ \ \ a,b,c \in R $$

De forma análoga, si elegimos a = 0, b = 1, c = 0, se obtiene:

$$ \begin{pmatrix} 0 & \color{red}{1} \\ 0 & 0 \end{pmatrix} \ \ \ \ a,b,c \in R $$

Como es imprescindible que un espacio vectorial contenga la matriz nula, podemos concluir que A no es un espacio vectorial.

En consecuencia, A no puede ser un subespacio de M(2,2,R).

Y así sucesivamente.