La unión de subespacios vectoriales

La unión de dos subespacios vectoriales, en general, no constituye un subespacio vectorial.

Sea V un espacio vectorial sobre un cuerpo K, y sean A y B dos de sus subespacios. Por lo general, la unión A ∪ B no forma un subespacio vectorial.

¿Por qué ocurre esto?

Porque la unión A ∪ B no está cerrada bajo la operación de suma vectorial:

$$ \vec{a} + \vec{b} \notin A \cup B $$

Solo está cerrada respecto a la multiplicación por escalares:

$$ k \cdot \vec{a} \in A \cup B $$

Demostración

Dado A y B subespacios de V, queremos determinar si su unión A ∪ B es también un subespacio vectorial.

$$ A \cup B $$

Para que A ∪ B sea un subespacio, debe cumplir - entre otras - la propiedad de cerradura bajo la suma: si $\vec{a}, \vec{b} \in A \cup B$, entonces debe cumplirse que $\vec{a} + \vec{b} \in A \cup B$.

$$ \forall \ \vec{a} \in A , \vec{b} \in B \Rightarrow \vec{a} + \vec{b} \in A \cup B $$

No obstante, esta afirmación es, en general, falsa.

Por tanto, A ∪ B no cumple los axiomas necesarios para ser un subespacio. 

Ejemplo práctico

Consideremos el espacio vectorial ℝ².

El plano cartesiano (x, y), compuesto por puntos de ℝ·ℝ ( ℝ² ), es un ejemplo típico de espacio vectorial.

Tomemos dos subespacios vectoriales X e Y, por ejemplo, el eje X y el eje Y:

$$ X = \left\{ \binom{x}{y} \in ℝ^2 \mid y = 0 \right\} $$

$$ Y = \left\{ \binom{x}{y} \in ℝ^2 \mid x = 0 \right\} $$

Ambos son subespacios vectoriales del plano V, ya que satisfacen los axiomas de subespacio y corresponden a sistemas lineales homogéneos.

Nota. Al ser subespacios unidimensionales, su representación gráfica es sencilla y facilita la comprensión del concepto.

La unión X ∪ Y incluye todos los vectores situados sobre el eje X o el eje Y (en azul):

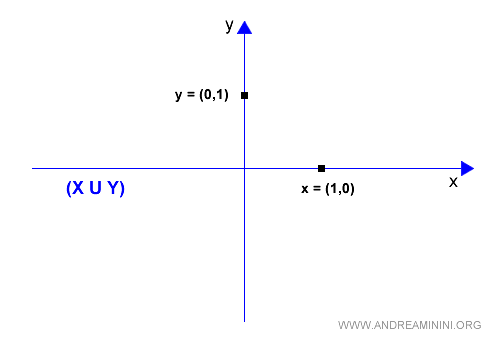
Sin embargo, dicha unión no es un subespacio vectorial, ya que no está cerrada bajo suma.

Veamos un contraejemplo:

Tomamos los vectores

$$ \vec{x} = \begin{pmatrix} 1 \\ 0 \end{pmatrix} \in X \qquad \vec{y} = \begin{pmatrix} 0 \\ 1 \end{pmatrix} \in Y $$

y los sumamos:

$$ \vec{x} + \vec{y} = \begin{pmatrix} 1 \\ 1 \end{pmatrix} $$

Queremos comprobar si $\vec{x} + \vec{y}$ pertenece a X ∪ Y:

Geométricamente es evidente que el punto $(1, 1)$ no se encuentra ni sobre el eje X ni sobre el eje Y.

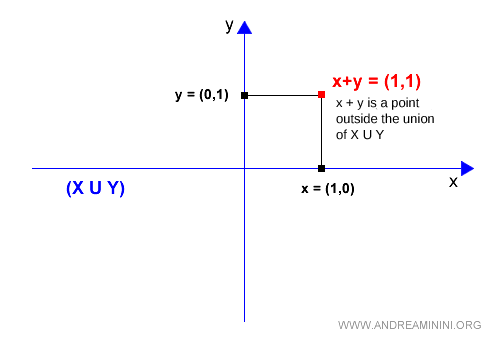
De hecho:

$$ \begin{pmatrix} 1 \\ 1 \end{pmatrix} \notin X \quad \text{ya que } y \ne 0 $$

$$ \begin{pmatrix} 1 \\ 1 \end{pmatrix} \notin Y \quad \text{ya que } x \ne 0 $$

Por tanto:

$$ \vec{x} + \vec{y} \notin X \cup Y $$

Así, la unión no cumple la propiedad de cerradura bajo suma.

Nota. La unión sí está cerrada bajo multiplicación escalar (pues $k\vec{x} \in X \cup Y$ si $\vec{x} \in X \cup Y$), pero eso no basta: un subespacio debe ser cerrado tanto bajo suma como bajo multiplicación.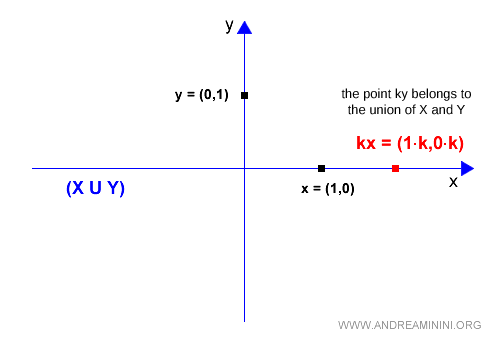

Esto demuestra que la unión de dos subespacios vectoriales no es, en general, un subespacio vectorial.

El subespacio más pequeño que contiene la unión

La suma A + B es el subespacio vectorial más pequeño de V que contiene la unión A ∪ B.

Demostración

Sean A y B subespacios de un espacio vectorial V:

$$ A, B \subseteq V $$

Sea L un subespacio vectorial que contiene la unión A ∪ B:

$$ A \cup B \subseteq L \subseteq V $$

Como L es subespacio, es cerrado bajo suma:

$$ \vec{a}, \vec{b} \in L \Rightarrow \vec{a} + \vec{b} \in L $$

Luego:

$$ \left\{ \vec{a} + \vec{b} \mid \vec{a} \in A, \ \vec{b} \in B \right\} \subseteq L $$

Por definición:

$$ A + B \subseteq L $$

Es decir, cualquier subespacio que contenga A y B debe contener también su suma A + B.

Y como A + B es en sí mismo un subespacio (véase demostración), se deduce que es el subespacio más pequeño que contiene la unión A ∪ B.

Explicación. El subespacio A + B está contenido en todo subespacio de V que incluya A y B, por lo que necesariamente es el menor de todos ellos.

Observaciones

Algunas observaciones adicionales sobre la unión de subespacios vectoriales:

• En general, la unión de dos subespacios vectoriales no es un subespacio. Sin embargo, hay casos particulares en los que sí lo es. Por ejemplo, si uno de los subespacios está contenido en el otro: $$ X \subseteq Y \Rightarrow X \cup Y = Y $$ En ese caso, la unión coincide con el mayor de los dos, y por tanto también es un subespacio.

Y así sucesivamente.