Intersección de subespacios vectoriales

La intersección de dos subespacios vectoriales es, a su vez, un subespacio vectorial.

Sea V un espacio vectorial sobre un cuerpo K, y sean A y B dos de sus subespacios. Entonces, la intersección A∩B también constituye un subespacio de V.

Demostración

Partimos de un espacio vectorial V y de dos de sus subespacios, A y B.

Queremos demostrar que la intersección A∩B es un subespacio vectorial.

Para ello, verificaremos que cumple los axiomas característicos de los subespacios vectoriales.

Nota: Un subespacio vectorial debe contener el vector cero y ser cerrado tanto bajo la suma de vectores como bajo la multiplicación por escalares.

1) Contención del vector nulo

Como A y B son subespacios, ambos contienen necesariamente el vector cero.

$$ \vec{0} \in A \qquad \vec{0} \in B $$

Por lo tanto, el vector nulo también pertenece a la intersección:

$$ \vec{0} \in A∩B $$

La intersección cumple así la primera condición para ser un subespacio vectorial.

2) Cerradura bajo la suma de vectores

Tomemos dos vectores cualesquiera en la intersección:

$$ \vec{a}, \vec{b} \in A∩B $$

Esto implica que ambos pertenecen simultáneamente a A y a B:

$$ \vec{a}, \vec{b} \in A \qquad \vec{a}, \vec{b} \in B $$

Dado que A y B están cerrados bajo la suma vectorial, se sigue que:

$$ \vec{a} + \vec{b} \in A \qquad \vec{a} + \vec{b} \in B $$

Es decir, la suma también pertenece a la intersección:

$$ \vec{a} + \vec{b} \in A∩B $$

Hemos comprobado, por tanto, que la intersección A∩B está cerrada bajo la suma de vectores.

3) Cerradura bajo la multiplicación por escalares

Sea $\vec{v} \in A∩B$ un vector cualquiera, y sea $\lambda \in K$ un escalar.

Dado que $\vec{v}$ pertenece tanto a A como a B, y ambos son subespacios cerrados bajo multiplicación escalar, se cumple que:

$$ \lambda \cdot \vec{v} \in A \qquad \lambda \cdot \vec{v} \in B $$

Por lo tanto, también:

$$ \lambda \cdot \vec{v} \in A∩B $$

Hemos demostrado que la intersección A∩B está cerrada bajo la multiplicación por escalares.

Conclusión

La intersección de dos subespacios contiene el vector nulo y cumple las propiedades de cerradura tanto para la suma vectorial como para la multiplicación por escalares. Por lo tanto, A∩B es un subespacio vectorial.

Además, A∩B es subespacio de A, de B, y también del espacio vectorial V del que A y B forman parte.

Un ejemplo práctico

El plano cartesiano xy puede considerarse un espacio vectorial V sobre el cuerpo K = ℝ².

Se trata de un plano bidimensional, ℝ×ℝ.

Los ejes coordenados X e Y constituyen subespacios vectoriales del espacio V.

Ambos son sistemas lineales homogéneos que incluyen el vector nulo.

$$ X = \left\{ \binom{x}{y} \in ℝ^2 \mid y = 0 \right\} $$

$$ Y = \left\{ \binom{x}{y} \in ℝ^2 \mid x = 0 \right\} $$

La intersección de los ejes X⋂Y se define del siguiente modo:

$$ X \cap Y = \left\{ \binom{x}{y} \in ℝ^2 \mid x = 0, \ y = 0 \right\} $$

En la práctica, esta intersección contiene únicamente el vector nulo.

$$ X \cap Y = \left\{ \vec{0} \right\} $$

Nota. Esto no implica que la intersección esté vacía: $$ X \cap Y \ne \Oslash $$. De hecho, no lo está, ya que contiene al menos un elemento: el vector nulo.

Desde un punto de vista gráfico, la intersección corresponde al origen O (en azul) del sistema cartesiano.

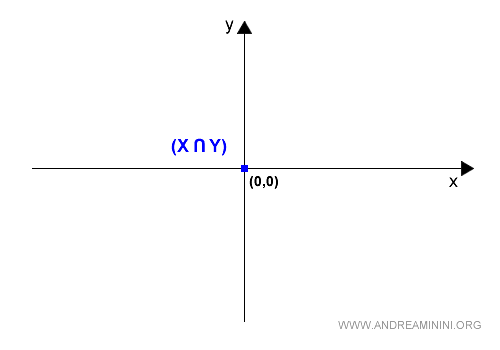
La presencia del vector nulo no basta, por sí sola, para garantizar que X⋂Y sea un subespacio vectorial.

Es necesario verificar que se cumplan también las demás propiedades fundamentales de los subespacios.

Propiedad 1 (cerradura bajo la suma de vectores)

Tomemos dos vectores cualesquiera en la intersección X⋂Y:

$$ \vec{x} \in X \cap Y \qquad \vec{y} \in X \cap Y $$

Dado que X⋂Y contiene únicamente el vector nulo, se deduce que:

$$ \vec{x} = \begin{pmatrix} 0 \\ 0 \end{pmatrix} \qquad \vec{y} = \begin{pmatrix} 0 \\ 0 \end{pmatrix} $$

La suma de dos vectores nulos es nuevamente el vector nulo:

$$ \vec{x} + \vec{y} = \begin{pmatrix} 0 \\ 0 \end{pmatrix} + \begin{pmatrix} 0 \\ 0 \end{pmatrix} = \begin{pmatrix} 0 \\ 0 \end{pmatrix} $$

Por tanto, la suma pertenece a la intersección:

$$ \vec{x} + \vec{y} \in X \cap Y $$

Queda así verificado que X⋂Y es cerrado bajo la suma vectorial.

Propiedad 2 (cerradura bajo la multiplicación escalar)

Sea $k \in ℝ$ un escalar cualquiera, y $\vec{x} \in X \cap Y$ un vector de la intersección.

Dado que $\vec{x}$ es necesariamente el vector nulo:

$$ \vec{x} = \begin{pmatrix} 0 \\ 0 \end{pmatrix} $$

El producto de un escalar por el vector nulo sigue siendo el vector nulo:

$$ k \cdot \vec{0} = k \cdot \begin{pmatrix} 0 \\ 0 \end{pmatrix} = \begin{pmatrix} 0 \\ 0 \end{pmatrix} $$

Así, el producto escalar también pertenece a la intersección:

$$ k \cdot \vec{0} \in X \cap Y $$

También se cumple la segunda propiedad característica de los subespacios.

Conclusión

La intersección de los ejes X e Y cumple con las propiedades requeridas: contiene el vector nulo, es cerrada bajo la suma y bajo la multiplicación escalar. Por lo tanto, es un subespacio vectorial.

En consecuencia, X⋂Y es un subespacio tanto de X como de Y, así como del espacio vectorial V (el plano cartesiano).

Observaciones

Algunas observaciones relevantes sobre la intersección de subespacios vectoriales:

• La intersección de dos subespacios vectoriales nunca es el conjunto vacío

  Demostración. Dado que X e Y son subespacios, ambos contienen por definición el vector nulo: $$ \vec{0} \in X \ , \ \vec{0} \in Y \ \Rightarrow\ \vec{0} \in X \cap Y $$ Por tanto, su intersección contiene al menos un elemento y no puede ser vacía. Puede ocurrir que contenga únicamente el vector nulo: $$ X \cap Y = \left\{ \vec{0} \right\} $$ pero nunca puede darse que: $$ X \cap Y = \Oslash $$