Span lineal

El span lineal (o envolvente lineal) de un conjunto de vectores $v_1, v_2, \dots, v_n$ en un espacio vectorial $V$ sobre un cuerpo $K$ es el conjunto formado por todas las combinaciones lineales posibles de dichos vectores con coeficientes escalares $\alpha_1, \alpha_2, \dots, \alpha_n$ pertenecientes a $K$: $$ \operatorname{Span}(v_1, \dots, v_n) = \left\{ \alpha_1 v_1 + \cdots + \alpha_n v_n \mid \alpha_i \in K \right\} $$

El span lineal también puede denotarse mediante las expresiones $L_k$, $L$ o utilizando corchetes angulares:

$$ L_k(v_1, \dots, v_n) \qquad L(v_1, \dots, v_n) \qquad \langle v_1, \dots, v_n \rangle $$

El conjunto $\operatorname{Span}(v_1, \dots, v_n)$ constituye un subespacio vectorial de $V$.

Este subespacio se conoce como el subespacio generado por los vectores $v_1, \dots, v_n$.

Ejemplos prácticos

Ejemplo 1

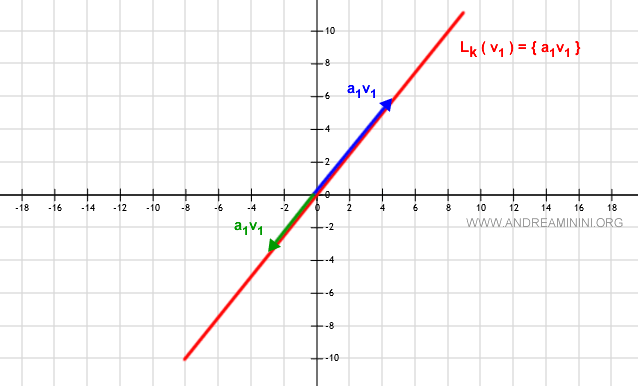
Sea $v_1$ un vector no nulo en el espacio vectorial $V$ sobre el cuerpo $\mathbb{R}^2$ ($v_1 \ne \vec{0}$). Entonces, el span lineal $L(v_1)$ está formado por todos los vectores de la forma $\alpha_1 v_1$ con $\alpha_1 \in \mathbb{R}$, es decir, todos los puntos de la recta que pasa por el origen y tiene la dirección de $v_1$.

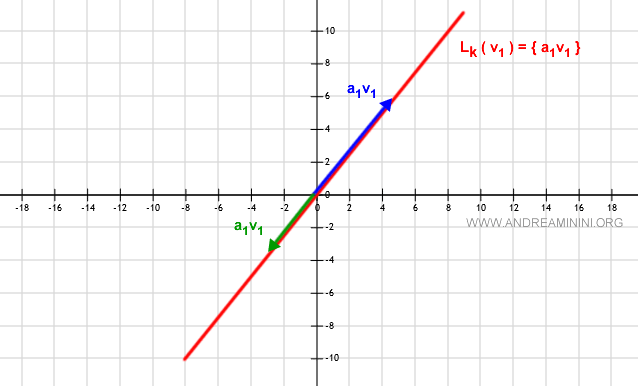
Cada valor de $\alpha_1$ genera un vector sobre la recta $L_k$ en la misma dirección que $v_1$, pero con módulo y orientación variables, ya que todos son múltiplos escalares de $v_1$.

Resulta evidente que $L_k$ es un subespacio vectorial de $V$.

Ejemplo 2

Sean $v_1$ y $v_2$ dos vectores en el espacio vectorial $V$ sobre el cuerpo $\mathbb{R}^2$. El span lineal $L_k(v_1, v_2)$ está constituido por todos los vectores de la forma $\alpha_1 v_1 + \alpha_2 v_2$, donde $\alpha_1, \alpha_2 \in \mathbb{R}$. Es decir, comprende todas las combinaciones lineales de $v_1$ y $v_2$ dentro del plano.

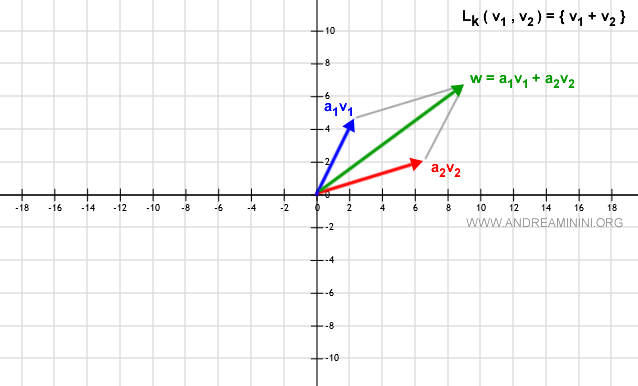
Cada par ordenado $(\alpha_1, \alpha_2)$ define un vector $w = \alpha_1 v_1 + \alpha_2 v_2$ con dirección, sentido y módulo variables.

Si los vectores $v_1$ y $v_2$ no son paralelos, el vector $w$ se obtiene aplicando la regla del paralelogramo: se suma un múltiplo escalar de $v_1$ con otro de $v_2$.

En este caso, el conjunto $L_k(v_1, v_2)$ constituye un subespacio bidimensional de $V$.

Nota. Si los vectores $v_1$ y $v_2$ son paralelos, el caso se reduce al de una única recta que pasa por el origen. Ambos vectores tienen la misma dirección y generan el mismo subespacio. En efecto, cualquier combinación lineal $\alpha_1 v_1 + \alpha_2 v_2$ será un múltiplo escalar de un solo vector. Por tanto: $$ \langle v_1, v_2 \rangle = \langle v_1 \rangle $$