Subespacio vectorial generado por un conjunto de vectores

El subespacio vectorial generado por un conjunto S de vectores en un espacio vectorial V $$ S = \{ v_1 , v_2, ... , v_n \} $$ es el subespacio más pequeño de V que contiene a todos los vectores de S. Se denota como L(S) o <S>: $$ L(S) \ \ \ o \ \ \ <S> $$ La letra L hace referencia a “lineal”.

El conjunto S, por sí solo, no constituye un subespacio vectorial.

$$ S = \{ v_1 , v_2, ... , v_n \} $$

El subespacio L(S) está formado por todas las combinaciones lineales posibles de los vectores del conjunto S:

$$ L(S) = \{ \lambda_1 v_1 + \lambda_2 v_2 + ... + \lambda_n v_n \ | \ v_i \in S, \ \lambda_i \in K \} $$

Explicación

Consideremos un espacio vectorial V.

Sea S un conjunto de vectores tomados de V:

$$ S = \{ v_1 , v_2, ... , v_n \} \subset V $$

En general, S no es un subespacio: simplemente es un conjunto de dos o más vectores.

El subespacio vectorial más pequeño que contiene a S se llama subespacio generado por S, y se representa con L(S) o <S>:

$$ L(S) \ \ \ o \ \ \ <S> $$

Este subespacio se construye a partir de todas las combinaciones lineales posibles de los n vectores de S con escalares pertenecientes al cuerpo K:

$$ L(S) = \{ k_1 \vec{v}_1 + k_2 \vec{v}_2 + ... + k_n \vec{v}_n \ \ | \ \vec{v}_i \in S, \ k_i \in K \} $$

Esta expresión también puede escribirse mediante sumatoria:

$$ L(S) = \left\{ \sum_{i=1}^n k_i \vec{v}_i \ \bigg| \ \vec{v}_i \in S \right\} $$

El subespacio L(S) incluye infinitos vectores (en general, $m \ge n$), todos obtenidos como combinaciones lineales de los n vectores originales del conjunto S.

Subespacio generado por un solo vector

Consideremos un único vector no nulo en el espacio:

$$ \vec{v} \in V \ , \ \vec{v} \ne 0 $$

En este caso, el conjunto S contiene solamente ese vector:

$$ S = \{ \vec{v} \} \subset V $$

Desde un punto de vista geométrico, el vector define una recta que pasa por el origen.

Así, el subespacio generado por S está formado por todos los múltiplos escalares de ese vector:

$$ L(\vec{v}) = \{ \lambda \vec{v} \ | \ \lambda \in K \} $$

Este subespacio contiene todos los vectores que yacen sobre la misma dirección.

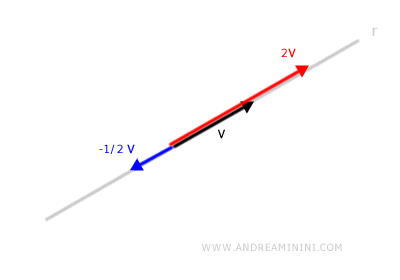
Todos los vectores del subespacio comparten la misma dirección, aunque pueden diferir en módulo y sentido.

Nota. En el caso particular en que el vector sea el vector nulo, el subespacio generado está formado únicamente por el vector nulo: $$ L(\vec{0}) = \{ \vec{0} \} $$ ya que cualquier escalar multiplicado por el vector nulo sigue dando como resultado el vector nulo.

Subespacio generado por dos vectores

El subespacio generado por dos vectores no nulos $\vec{v}_1$ y $\vec{v}_2$ en un espacio vectorial $V$ sobre un cuerpo $K$

$$ v_1, v_2 \in V \ , \ v_1,v_2 \ne \vec{0} $$

depende de si estos vectores son linealmente dependientes o independientes.

• Si los dos vectores son paralelos
  En este caso, los vectores son linealmente dependientes: uno puede expresarse como un múltiplo escalar del otro. $$ \vec{v}_1 = \lambda \cdot \vec{v}_2 \ \ \lambda \in K $$ Ambos tienen la misma dirección y pertenecen a una misma recta.
  
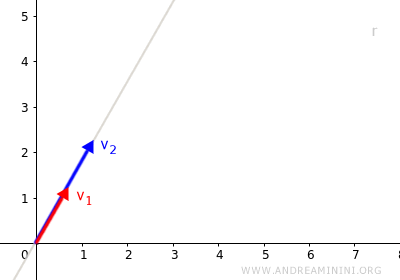
  Por lo tanto, todas sus combinaciones lineales siguen estando sobre esa misma recta: $$ L(\vec{v}_1 , \vec{v}_2) = \{ \lambda_1 \vec{v}_1 + \lambda_2 \vec{v}_2 \ | \ \lambda_1, \lambda_2 \in K \} $$
• Si los dos vectores no son paralelos
  En este caso, los vectores son linealmente independientes: ninguno puede escribirse como múltiplo del otro. $$ \vec{v}_1 \ne \lambda \cdot \vec{v}_2 \ \ \lambda \in K $$ Tienen direcciones distintas y determinan un plano.
  
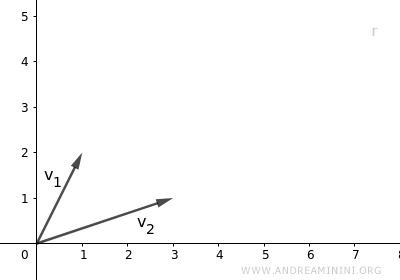
  Sus combinaciones lineales generan todos los vectores del plano definido por $\vec{v}_1$ y $\vec{v}_2$: $$ L(\vec{v}_1 , \vec{v}_2) = \{ \lambda_1 \vec{v}_1 + \lambda_2 \vec{v}_2 \ | \ \lambda_1, \lambda_2 \in K \} $$

Ejemplo

Sea el conjunto de vectores

$$ S = \{ \vec{v}_1, \vec{v}_2 \} $$

con:

$$ \vec{v}_1 = \begin{pmatrix} 1 \\ 2 \end{pmatrix} $$

$$ \vec{v}_2 = \begin{pmatrix} 3 \\ 1 \end{pmatrix} $$

Desde un punto de vista geométrico, estos vectores no son paralelos, por lo que son linealmente independientes.

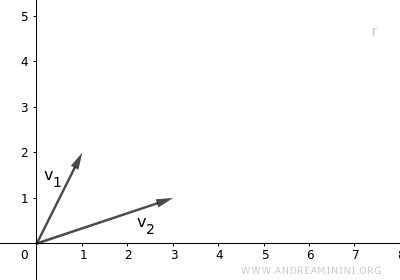
Este conjunto pertenece al espacio vectorial $V = \mathbb{R}^2$:

$$ S \subset V = \mathbb{R}^2 $$

El subespacio generado por $S$ es el plano que contiene todas las combinaciones lineales de $\vec{v}_1$ y $\vec{v}_2$:

$$ L(S) = \lambda_1 \cdot \vec{v}_1 + \lambda_2 \cdot \vec{v}_2 $$

$$ L(S) = \lambda_1 \cdot \begin{pmatrix} 1 \\ 2 \end{pmatrix} + \lambda_2 \cdot \begin{pmatrix} 3 \\ 1 \end{pmatrix} $$

donde $\lambda_1$ y $\lambda_2$ son escalares reales arbitrarios.

Este subespacio está compuesto por todos los vectores obtenidos mediante combinaciones lineales de $\vec{v}_1$ y $\vec{v}_2$.

Nota. Si tomamos $\lambda_1 = 2$ y $\lambda_2 = 3$, obtenemos el siguiente vector: $$ \vec{v}_n = \lambda_1 \cdot \vec{v}_1 + \lambda_2 \cdot \vec{v}_2 $$ $$ \vec{v}_n = 2 \cdot \begin{pmatrix} 1 \\ 2 \end{pmatrix} + 3 \cdot \begin{pmatrix} 3 \\ 1 \end{pmatrix} $$ $$ \vec{v}_n = \begin{pmatrix} 2 \\ 4 \end{pmatrix} + \begin{pmatrix} 9 \\ 3 \end{pmatrix} $$ $$ \vec{v}_n = \begin{pmatrix} 11 \\ 7 \end{pmatrix} $$ Desde una perspectiva geométrica:

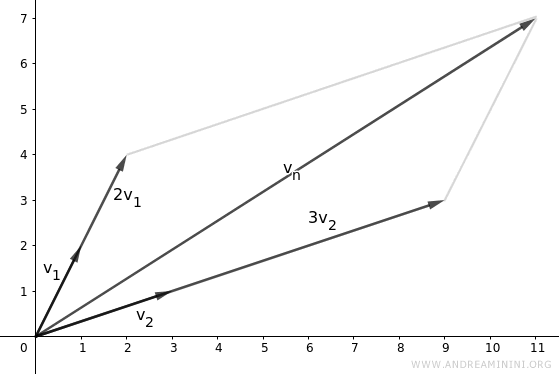
Y así sucesivamente.