Espacio vectorial de vectores geométricos aplicados
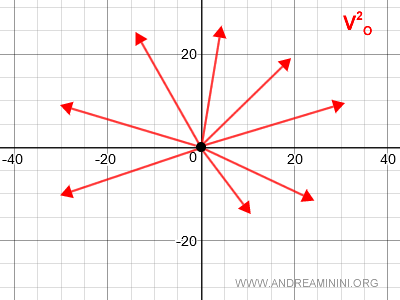
El espacio vectorial de los vectores geométricos aplicados en un plano con origen en el punto O está formado por todos los vectores que parten de O y terminan en cualquier otro punto del plano.
Explicación
Dado un punto O en el plano, el conjunto de todos los vectores con origen en O constituye un espacio vectorial que se denota por V2O.
¿Qué se entiende por vector aplicado en O? Es un vector del tipo OP, donde el punto inicial es O y el terminal es un punto P cualquiera del plano.
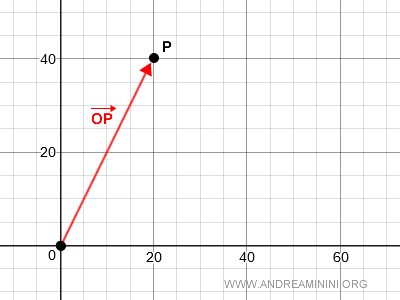
En el espacio V2O se pueden realizar operaciones básicas como la suma de vectores y la multiplicación por escalares, cumpliendo todas las propiedades propias de un espacio vectorial real.
Suma de vectores
Dados dos vectores OP y OQ, su suma se obtiene construyendo el paralelogramo definido por ellos y considerando su diagonal:
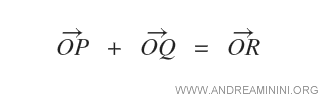
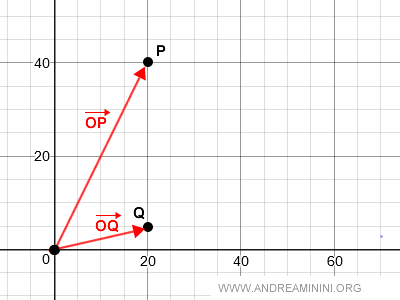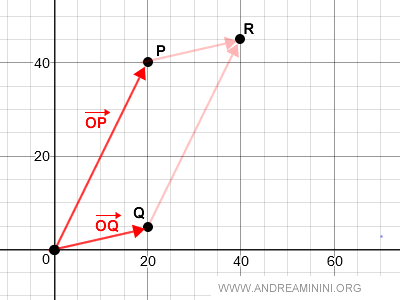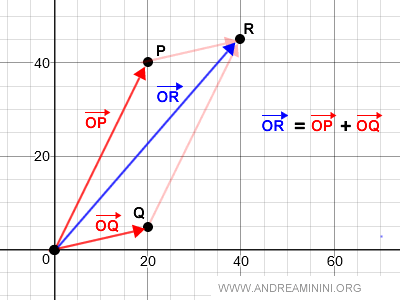
Según la regla del paralelogramo, el vector suma corresponde a la diagonal O → R del paralelogramo OPRQ.
La representación gráfica de esta operación es la siguiente:
Multiplicación escalar
Dado un vector OP y un escalar α, su producto es un nuevo vector OQ, con el mismo origen O y un extremo Q tal que la longitud de OQ es proporcional a la de OP, en función del valor de α.
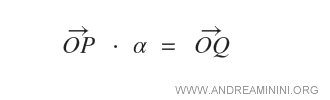
El módulo del vector OQ se obtiene mediante la relación:
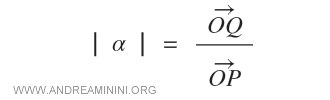
Gráficamente, la multiplicación escalar se representa así en el plano:
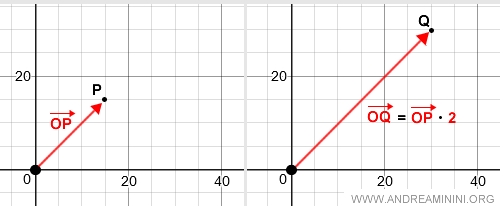
Según el signo del escalar α, el vector OQ tendrá la misma dirección que OP (si α es positivo) o la dirección opuesta (si α es negativo).
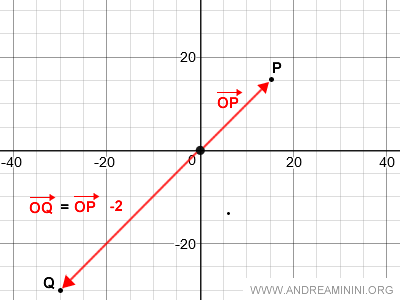
En ambos casos, los vectores OQ y OP son colineales, ya que comparten la misma dirección (línea de acción), y el valor absoluto del escalar α determina la razón entre sus módulos.
Casos particulares
Si α = 1, el producto escalar no modifica el vector: OQ coincide con OP.
Si α = - 1, se obtiene el vector opuesto, es decir, OQ apunta en dirección contraria a OP y el punto Q es simétrico de P respecto a O.
Si α = 0, el resultado es el vector nulo, que tiene origen y extremo en el mismo punto O: OO.