Distancia de un punto a una recta

La distancia de un punto P a una recta es la longitud del segmento que une el punto P con el pie de la perpendicular trazada desde P sobre la recta (P').

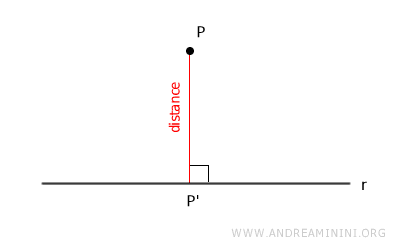
Dicho de otro modo, esta distancia corresponde a la longitud de la proyección ortogonal del punto sobre la recta.

Es, por definición, el trayecto más corto entre el punto y la recta. Cualquier otro segmento oblicuo que vaya de P hasta otro punto sobre la recta siempre será más largo que esta distancia mínima.

Demostración

Para demostrarlo, consideremos un punto cualquiera sobre la recta distinto de P', por ejemplo, el punto A.

El segmento AP, que une los puntos P y A, forma un ángulo oblicuo respecto a la perpendicular.

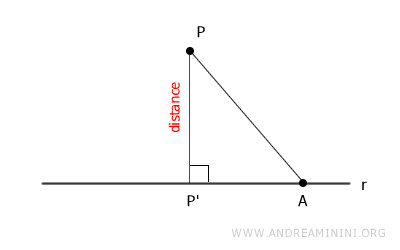
La longitud del segmento AP es necesariamente mayor que la del segmento PP' (la distancia buscada), ya que los puntos P, P' y A determinan un triángulo rectángulo.

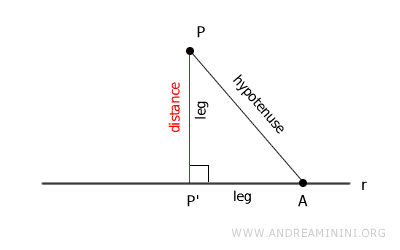
De acuerdo con el teorema de Pitágoras, en todo triángulo rectángulo, cualquiera de los catetos es siempre más corto que la hipotenusa.

Por tanto, el segmento AP nunca puede representar la distancia entre el punto P y la recta r, puesto que la longitud de PP' es la mínima posible.

Este razonamiento se cumple para cualquier segmento AP en el que A sea un punto distinto de P' sobre la recta r.

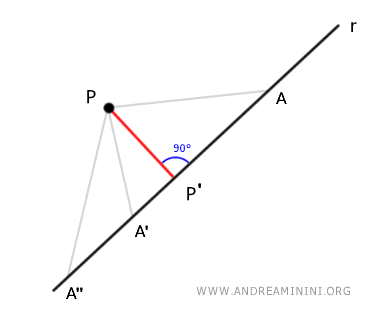
Si te interesa profundizar en el cálculo de la distancia entre un punto y una recta mediante ecuaciones vectoriales, puedes consultar otra de mis notas universitarias: cómo calcular la distancia entre un punto y una recta con vectores. El resto de esta nota se limita al plano y a los fundamentos de la geometría analítica de nivel bachillerato.

Cálculo de la distancia entre un punto y una recta en el plano

En geometría analítica, la distancia entre un punto P(x₀, y₀) y una recta r en el plano se determina con la siguiente fórmula: $$ d = \frac{|ax_0 + by_0 + c|}{\sqrt{a^2 + b^2}} $$

Donde $ ax + by + c = 0 $ es la ecuación general de la recta r, y (x₀, y₀) son las coordenadas del punto P.

Ejemplo práctico

Veamos el caso de la siguiente recta en el plano cartesiano:

$$ 2x + 4y - 6 = 0 $$

y del punto A, cuyas coordenadas son:

$$ A \begin{pmatrix} 3 \\ 2 \end{pmatrix} $$

Para mayor claridad, vamos a representar gráficamente tanto el punto A como la recta en el plano cartesiano.

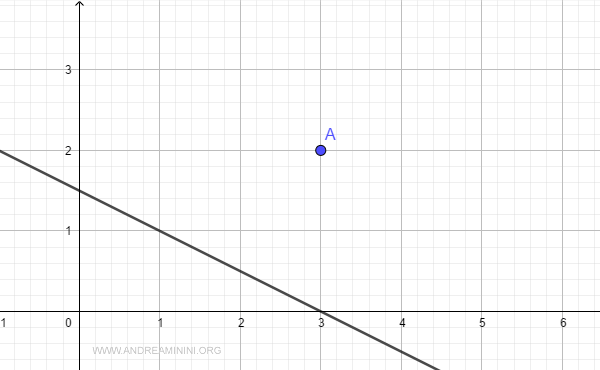
¿Cuál es la distancia entre el punto y la recta?

Para calcular la distancia entre el punto A y la recta r, utilizamos la fórmula indicada:

$$ d = \frac{|ax_0 + by_0 + c|}{\sqrt{a^2 + b^2}} $$

Sustituimos las coordenadas del punto A(x₀, y₀) = (3, 2), es decir, x₀ = 3 y y₀ = 2, en la fórmula:

$$ d = \frac{|a(3) + b(2) + c|}{\sqrt{a^2 + b^2}} $$

Así como los coeficientes de la ecuación general de la recta $ 2x + 4y - 6 = 0 $, que son a = 2, b = 4 y c = -6:

$$ d = \frac{|2 \cdot 3 + 4 \cdot 2 - 6|}{\sqrt{2^2 + 4^2}} $$

Realizamos las operaciones paso a paso:

$$ d = \frac{|6 + 8 - 6|}{\sqrt{4 + 16}} $$

$$ d = \frac{8}{\sqrt{20}} $$

$$ d = 1.78 $$

Por lo tanto, la distancia mínima entre el punto A y la recta es de 1.78 unidades.

Una verificación rápida en GeoGebra confirma que el cálculo es correcto. La distancia d corresponde al segmento AH, perpendicular (de 90°) a la recta, cuyo extremo se encuentra en el punto A(3, 2), y mide aproximadamente 1.78 unidades.

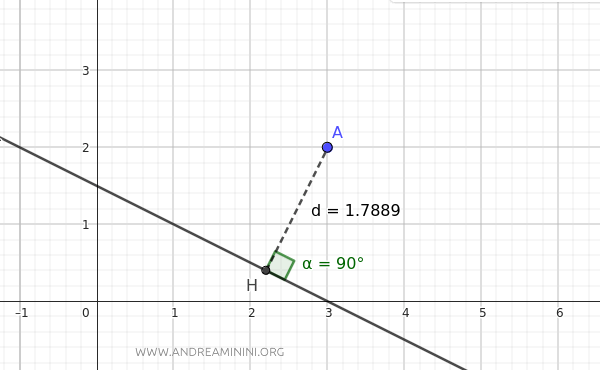
Demostración

Para demostrar la fórmula de la distancia, consideremos la recta $ ax + by + c = 0 $ y un punto cualquiera en el plano $ P(x_0, y_0) $.

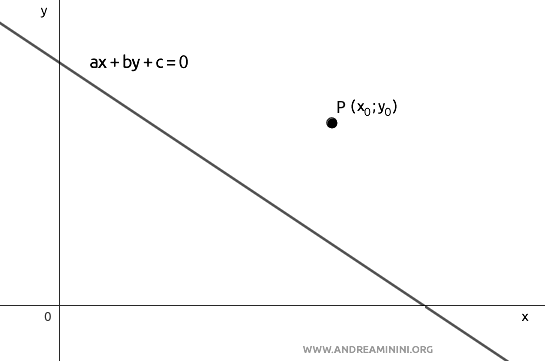
Sabemos que, desde un punto de vista geométrico, la distancia es el segmento $ \overline{PH} $, perpendicular a la recta, cuyos extremos son el punto P y un punto $ H $ sobre la recta.

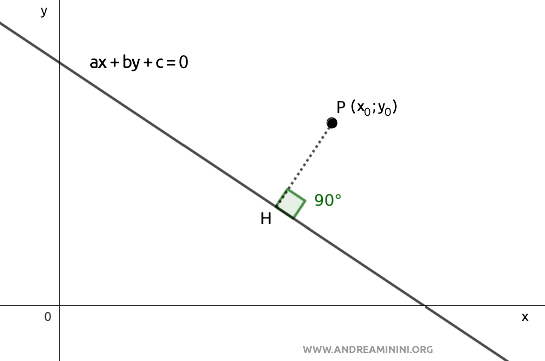
Para ello, trazamos dos rectas paralelas a los ejes cartesianos que pasan por el punto P.

De esta manera, se obtienen dos puntos de intersección, A y B, sobre la recta.

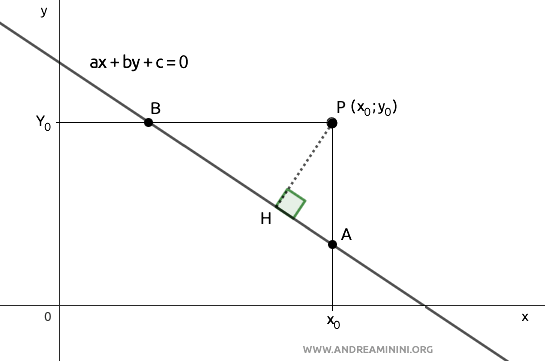
El punto A pertenece a la recta $ ax + by + c = 0 $ y comparte la misma coordenada x₀ que el punto P.

Por tanto, sustituimos x por x₀ en la ecuación general de la recta:

$ ax_0 + by + c = 0 $

De ahí podemos despejar el valor de y:

$$ y = \frac{-ax_0 - c}{b} = - \frac{ax_0 + c}{b} $$

Con esto, obtenemos las coordenadas del punto A:

$$ A = \bigg( x_0 ; - \frac{ax_0 + c}{b} \bigg) $$

De manera análoga, determinamos el punto B.

El punto B también pertenece a la recta $ ax + by + c = 0 $ y comparte la misma coordenada y₀ que el punto P.

Por ello, sustituimos y por y₀ en la ecuación de la recta:

$ ax + by_0 + c = 0 $

Y despejamos el valor de x:

$$ x = \frac{-by_0 - c}{a} = - \frac{by_0 + c}{a} $$

Así, obtenemos las coordenadas del punto B:

$$ B = \bigg( - \frac{by_0 + c}{a} ; y_0 \bigg) $$

En el plano, los puntos A, B y P forman un triángulo ABP.

Este triángulo ABP es un triángulo rectángulo, pues sus lados coinciden con rectas paralelas a los ejes cartesianos, formando entre sí un ángulo recto.

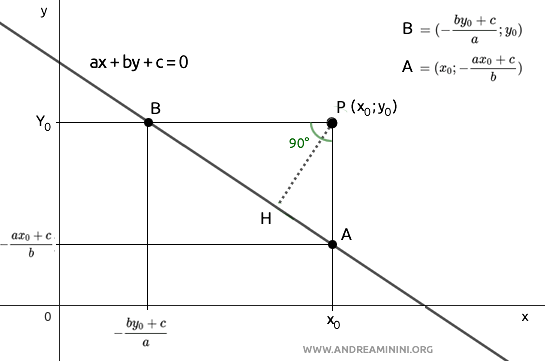
En un triángulo rectángulo, la altura $ \overline{PH} $ relativa a la hipotenusa es igual al cociente entre el producto de los catetos $ \overline{AP} \cdot \overline{BP} $ y la longitud de la hipotenusa $ \overline{AB} $:

$$ \overline{PH} = \frac{\overline{AP} \cdot \overline{BP}}{\overline{AB}} $$

Explicación: Esta fórmula se deduce del hecho de que, en cualquier triángulo, la altura se obtiene dividiendo el doble del área entre la base. $$ h = \frac{2 \times \text{área}}{\text{base}} $$ En el caso del triángulo rectángulo, el área es la mitad del producto de sus catetos, y considerando la hipotenusa como base, resulta: $$ h = \frac{2 \times \left( \frac{\overline{AP} \cdot \overline{BP}}{2} \right)}{\overline{AB}} $$ $$ h = \frac{\overline{AP} \cdot \overline{BP}}{\overline{AB}} $$

Para determinar la distancia PH, necesitamos calcular primero las longitudes de los segmentos AP, BP y AB.

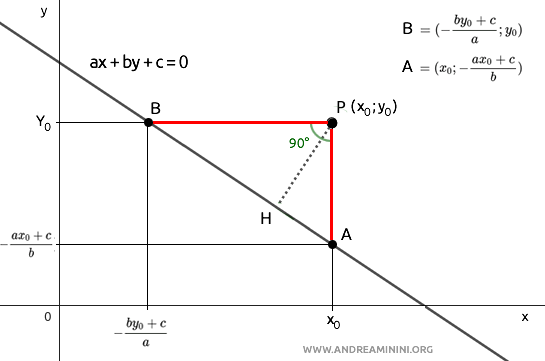
Obtener las longitudes de los catetos AP y BP es sencillo, dado que conocemos las coordenadas de A y B:

$$ \overline{AP} = \bigg| y_0 - \left( - \frac{ax_0 + c}{b} \right) \bigg| = \bigg| \frac{ax_0 + by_0 + c}{b} \bigg| $$

$$ \overline{BP} = \bigg| x_0 - \left( - \frac{by_0 + c}{a} \right) \bigg| = \bigg| \frac{ax_0 + by_0 + c}{a} \bigg| $$

Para calcular la hipotenusa AB, aplicamos el teorema de Pitágoras y simplificamos:

$$ \overline{AB} = \sqrt{\overline{AP}^2 + \overline{BP}^2} $$

$$ \overline{AB} = \sqrt{ \left( \bigg| \frac{ax_0 + by_0 + c}{b} \bigg| \right)^2 + \left( \bigg| \frac{ax_0 + by_0 + c}{a} \bigg| \right)^2 } $$

$$ \overline{AB} = \sqrt{ \frac{(ax_0 + by_0 + c)^2}{b^2} + \frac{(ax_0 + by_0 + c)^2}{a^2} } $$

$$ \overline{AB} = \big| ax_0 + by_0 + c \big| \cdot \sqrt{ \frac{1}{b^2} + \frac{1}{a^2} } $$

$$ \overline{AB} = \big| ax_0 + by_0 + c \big| \cdot \sqrt{ \frac{a^2 + b^2}{a^2 b^2} } $$

$$ \overline{AB} = \frac{ \big| ax_0 + by_0 + c \big| }{ |ab| } \cdot \sqrt{ a^2 + b^2 } $$

Una vez conocidas las longitudes de AP, BP y AB, las sustituimos en la fórmula para hallar la distancia PH:

$$ \overline{PH} = \frac{\overline{AP} \cdot \overline{BP}}{\overline{AB}} $$

$$ \overline{PH} = \frac{ \big| \frac{ax_0 + by_0 + c}{b} \big| \cdot \big| \frac{ax_0 + by_0 + c}{a} \big| }{ \frac{ \big| ax_0 + by_0 + c \big| }{ |ab| } \cdot \sqrt{ a^2 + b^2 } } $$

$$ \overline{PH} = \big| \frac{ax_0 + by_0 + c}{b} \big| \cdot \big| \frac{ax_0 + by_0 + c}{a} \big| \cdot \frac{ |ab| }{ \big| ax_0 + by_0 + c \big| \cdot \sqrt{ a^2 + b^2 } } $$

Recordemos que el valor absoluto de un producto |ab| equivale al producto de los valores absolutos |a|·|b|:

$$ \overline{PH} = \bigg| \frac{ax_0 + by_0 + c}{b} \bigg| \cdot \bigg| \frac{ax_0 + by_0 + c}{a} \bigg| \cdot \frac{ |a| \cdot |b| }{ \big| ax_0 + by_0 + c \big| \cdot \sqrt{ a^2 + b^2 } } $$

Y que el valor absoluto de un cociente es el cociente de los valores absolutos.

$$ \overline{PH} = \frac{ |ax_0 + by_0 + c| }{ |b| } \cdot \frac{ |ax_0 + by_0 + c| }{ |a| } \cdot \frac{ |a| \cdot |b| }{ |ax_0 + by_0 + c| \cdot \sqrt{ a^2 + b^2 } } $$

Al simplificar, se obtiene:

$$ \require{cancel} \overline{PH} = \frac{ |ax_0 + by_0 + c| }{ \cancel{ |b| } } \cdot \frac{ \cancel{ |ax_0 + by_0 + c| } }{ \cancel{ |a| } } \cdot \frac{ \cancel{ |a| } \cdot \cancel{ |b| } }{ \cancel{ |ax_0 + by_0 + c| } \cdot \sqrt{ a^2 + b^2 } } $$

Y, finalmente, llegamos a la fórmula buscada para la distancia entre el punto y la recta:

$$ \require{cancel} \overline{PH} = \frac{ |ax_0 + by_0 + c| }{ \sqrt{ a^2 + b^2 } } $$

Así queda demostrada la fórmula.