Cálculo de la distancia entre un punto y una recta utilizando vectores
La distancia más corta entre un punto P y una recta es la longitud del segmento perpendicular PH, donde P(x0; y0) es el punto dado y H es el pie de la perpendicular sobre la recta.
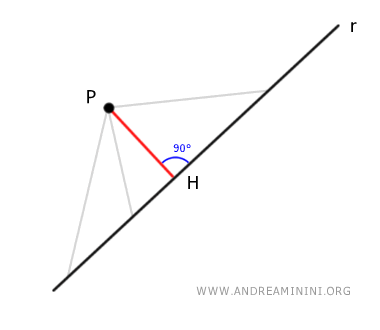
Para calcular la longitud del segmento PH, se emplea la siguiente fórmula: $$ D(P(x_0,y_0),r) = \frac{|ax_0+by_0+c|}{\sqrt{a^2+b^2}} $$
Ejemplo práctico
En el plano cartesiano, consideremos la recta r
$$ 2x + 4y -6 = 0 $$
y el punto A
$$ A \begin{pmatrix} 3 \\ 2 \end{pmatrix} $$
Representemos gráficamente la recta y el punto en el plano cartesiano:
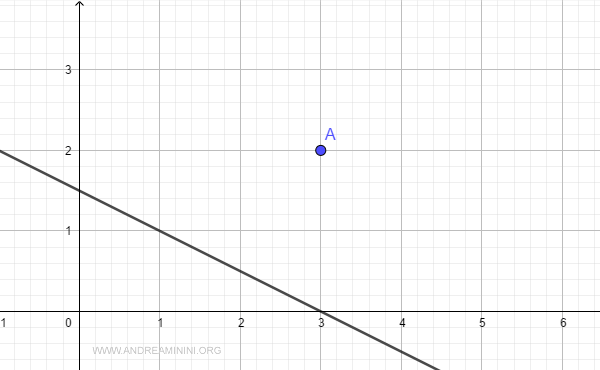
¿Cuál es la distancia más corta entre el punto y la recta?
Para determinar la distancia entre el punto A y la recta r, utilizamos la fórmula:
$$ D(A(x_0,y_0),r) = \frac{|ax_0+by_0+c|}{\sqrt{a^2+b^2}} $$
Sustituyendo las coordenadas del punto A:
$$ D(A(3,2),r) = \frac{|a(3)+b(2)+c|}{\sqrt{a^2+b^2}} $$
Y los coeficientes de la recta:
$$ D(A(3,2),r) = \frac{|2 \cdot 3 + 4 \cdot 2 -6|}{\sqrt{2^2+4^2}} = \frac{|6+8-6|}{\sqrt{4+16}} = \frac{8}{\sqrt{20}} = 1.78 $$
Por lo tanto, la distancia más corta entre el punto A y la recta es 1.78.
¿Cuál es el punto sobre la recta más cercano al punto A?
Una vez conocida la distancia más corta entre el punto A y la recta,
queremos ahora determinar cuál es el punto sobre la recta que se encuentra más próximo a A.
Este punto se sitúa sobre una recta perpendicular a r que pasa por el punto A.
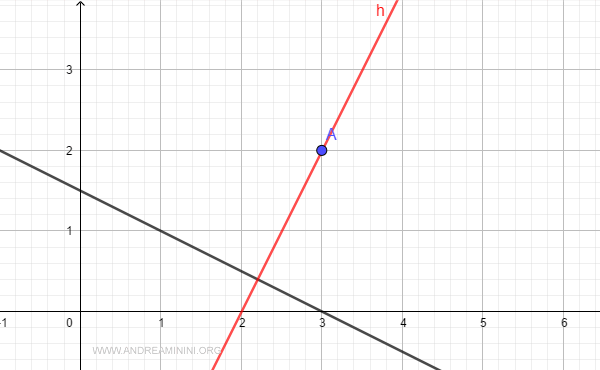
La ecuación vectorial de la recta perpendicular r' es:
$$ \begin{pmatrix} x \\ y \end{pmatrix} = \begin{pmatrix} 3 \\ 2 \end{pmatrix} + t \cdot \begin{pmatrix} 2 \\ 4 \end{pmatrix} $$
Nota: Las coordenadas (3,2) corresponden al punto A, y el vector (2,4) es el vector normal, perpendicular al vector director de la recta.
Transformando la ecuación vectorial en forma paramétrica:
$$ \begin{cases} x = 3 + 2t \\ y = 2 + 4t \end{cases} $$
El punto sobre la recta más cercano a A debe cumplir esta ecuación.
Añadimos, como condición adicional, la ecuación de la recta r:
$$ \begin{cases} x = 3 + 2t \\ y = 2 + 4t \\ 2x + 4y -6 = 0 \end{cases} $$
Resolvemos el sistema para t:
$$ \begin{cases} x = 3 + 2t \\ y = 2 + 4t \\ 2(3+2t) + 4(2+4t) -6 = 0 \end{cases} $$
$$ \begin{cases} x = 3 + 2t \\ y = 2 + 4t \\ 6 + 4t + 8 +16t -6 = 0 \end{cases} $$
$$ \begin{cases} x = 3 + 2t \\ y = 2 + 4t \\ 8 + 20t = 0 \end{cases} $$
$$ \begin{cases} x = 3 + 2t \\ y = 2 + 4t \\ t = \frac{-8}{20} = \frac{-2}{5} \end{cases} $$
Así, hemos hallado el valor del parámetro t para la recta perpendicular r'.
Para obtener las coordenadas del punto H sobre la recta, el más cercano al punto A, sustituimos el valor de t en las ecuaciones paramétricas:
$$ \begin{cases} x = 3 + 2t \\ y = 2 + 4t \end{cases} $$
$$ \begin{cases} x = 3 + 2 \cdot \frac{-2}{5} \\ y = 2 + 4 \cdot \frac{-2}{5} \end{cases} $$
$$ \begin{cases} x = \frac{15 - 4}{5} \\ y = \frac{10 - 8}{5} \end{cases} $$
$$ \begin{cases} x = \frac{11}{5} = 2.2 \\ y = \frac{2}{5} = 0.4 \end{cases} $$
Así, obtenemos las coordenadas del punto H sobre la recta.
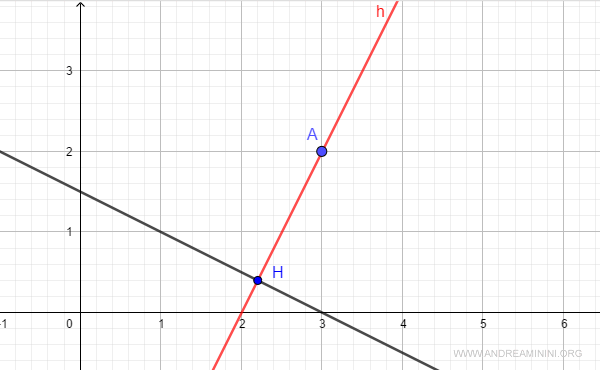
Nota: Para comprobar el resultado, podemos calcular la distancia entre los puntos A y H. Si el cálculo es correcto, esta distancia debe coincidir con la distancia entre el punto A y la recta r. $$ || A-H || = || \begin{pmatrix} 3 - \frac{11}{5} \\ 2 - \frac{2}{5} \end{pmatrix} || = || \begin{pmatrix} \frac{4}{5} \\ \frac{8}{5} \end{pmatrix} || = $$ $$ || A-H || = \sqrt{\left(\frac{4}{5}\right)^2 + \left(\frac{8}{5}\right)^2} = \sqrt{\frac{16}{25} + \frac{64}{25}} = \sqrt{\frac{16}{5}} = 1.78 $$ Perfecto, coincide.
¡Y listo!