Vectores axiales (seudovectores)
Un vector axial, también llamado seudovector, es una magnitud vectorial que permanece invariante bajo una reflexión espacial, es decir, bajo una transformación de paridad.
Los vectores axiales se comportan igual que los vectores ordinarios cuando el sistema gira, pero reaccionan de forma distinta cuando se invierten las coordenadas espaciales mediante una transformación de paridad (véase el operador de paridad).
Dicho de otro modo, bajo una transformación de paridad, un vector ordinario o polar invierte su orientación, mientras que un vector axial permanece inalterado.
Para comprender bien esta diferencia, conviene analizar un ejemplo concreto.
Un ejemplo práctico
Ejemplo de un vector ordinario
Consideremos un vector ordinario $ \vec v $.
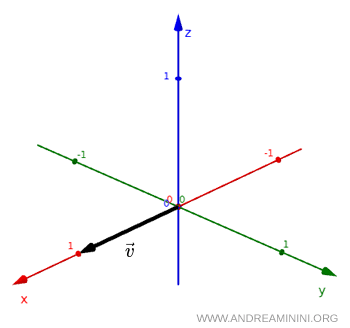
Si realizamos una inversión espacial, es decir, $ x \to -x $ y $ y \to -y $, el vector se transforma en su vector opuesto $ - \vec v $.
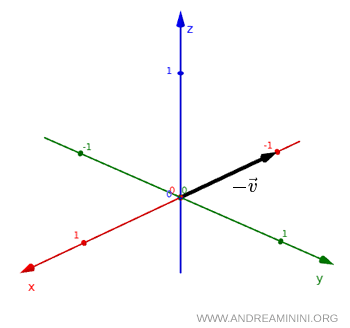
El nuevo vector $ - \vec v $ conserva el mismo módulo y la misma dirección geométrica, pero su orientación se invierte con respecto al vector original $ \vec v $.
En otras palabras, el vector cambia de signo cuando se aplica una inversión espacial.
Esto significa que, al observar un vector ordinario en un sistema de referencia reflejado, su magnitud permanece intacta mientras que su orientación se invierte.
Nota. Ejemplos habituales de vectores ordinarios en física son el desplazamiento, la velocidad y la fuerza.
En cambio, un vector axial se comporta de manera diferente: permanece invariante bajo una reflexión espacial.
Ejemplo de un vector axial
Un ejemplo clásico de vector axial es el momento angular.
Si consideramos un vector posición $ \vec r $ y un vector cantidad de movimiento $ \vec p $, el momento angular se define como su producto vectorial:
$$ \vec L = \vec r \times \vec p $$
En general, el producto vectorial de dos vectores polares da siempre como resultado un vector axial.
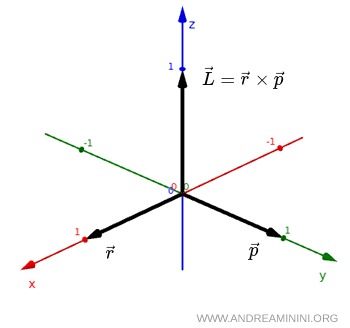
Si el sistema se observa mediante una reflexión espacial, los vectores $ \vec r $ y $ \vec p $ se transforman en $ - \vec r $ y $ - \vec p $, respectivamente. Sin embargo, su producto vectorial conserva la misma orientación.
$$ \vec L = \vec r \times \vec p = ( - \vec r ) \times ( - \vec p ) $$
En ambos casos, el vector $ \vec L $ es perpendicular al plano definido por $ \vec r $ y $ \vec p $, y apunta en la misma dirección a lo largo del eje $ z $.
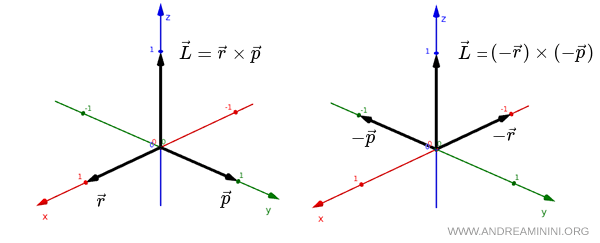
Por lo tanto, el vector axial $ \vec L $ no cambia de signo bajo una inversión espacial.
Nota. Otros ejemplos de vectores axiales en física son la velocidad angular, el torque y el campo magnético. Todos ellos surgen de un producto vectorial.
¿Cuál es el significado físico de los vectores axiales?
Los vectores axiales revelan una propiedad fundamental del espacio: ciertas magnitudes físicas no dependen solo de la dirección, sino también de la orientación del propio espacio.
Por esta razón desempeñan un papel central en los fenómenos relacionados con la paridad, especialmente en el contexto de las interacciones fundamentales.
En particular, resultan esenciales para comprender la violación de la paridad en la interacción débil.
Y así sucesivamente.