Cantidad de movimiento en física

¿Qué es la cantidad de movimiento?

La cantidad de movimiento se define como el producto de la masa (m) de un objeto por su velocidad (v): $$ \vec{p} = m \cdot \vec{v} $$

Es una magnitud vectorial, ya que surge de multiplicar un escalar (la masa) por un vector (la velocidad).

A diferencia de la velocidad, la cantidad de movimiento incorpora también la masa del cuerpo que se desplaza.

¿Por qué es importante?

La cantidad de movimiento indica la fuerza necesaria para detener un objeto en movimiento en un tiempo determinado.

Para frenar un cuerpo, su cantidad de movimiento debe anularse. Cuanto mayor sea la cantidad de movimiento inicial, mayor será la fuerza necesaria, siempre que el tiempo de frenado sea el mismo.

$$ \vec{F} = \vec{p} = m \cdot \vec{v} $$

Un ejemplo cotidiano: las barreras de seguridad de una autopista deben diseñarse para absorber y detener el avance de un vehículo que se desvía de la calzada.

La cantidad de movimiento también mide el efecto que un cuerpo en movimiento puede ejercer al colisionar o interactuar con otro.

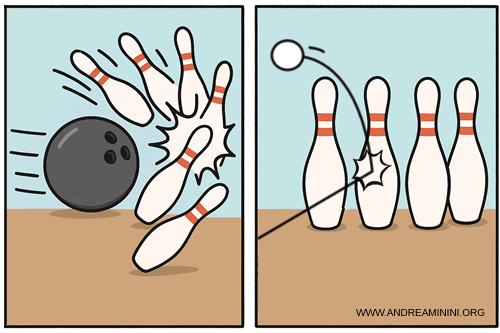
Una bola de bolos, por ejemplo, puede derribar los bolos con facilidad incluso a baja velocidad gracias a su gran masa y, por tanto, a su elevada cantidad de movimiento. En cambio, una pelota de ping-pong, aunque viaje mucho más rápido, apenas ejerce efecto alguno porque su masa minúscula le otorga una cantidad de movimiento casi nula.

La unidad de la cantidad de movimiento. Se obtiene analizando las dimensiones de la fórmula: $$ \vec{p} = m \cdot \vec{v} = [M] \cdot [V] = [M] \cdot \frac{[L]}{[T]} $$ En el SI, la masa [M] se mide en kilogramos, la longitud [L] en metros y el tiempo [T] en segundos. La unidad es, por tanto, kg·m·s^-1. $$ \vec{p} = [M] \cdot \frac{[L]}{[T]} = kg \cdot \frac{m}{s} = kg \cdot m \cdot s^{-1} $$ También puede expresarse en newton-segundos, dado que 1 N = 1 kg·m·s^-2: $$ \vec{p} = [M] \cdot \frac{[L]}{[T]} = (kg \cdot m \cdot s^{-2}) \cdot s = Ns $$ Es la misma unidad que el impulso de una fuerza.

Un ejemplo práctico

Ejemplo 1

Un coche de masa $m = 1000 \,\text{kg}$ circula a $v = 20 \,\text{m/s}$ (aproximadamente 72 km/h).

Su cantidad de movimiento es de veinte mil kilogramo-metros por segundo:

$$ p = m v = 1000 \cdot 20 = 20{,}000 \,\text{kg·m/s} $$

Para detenerlo, es necesario reducir esa cantidad de movimiento a cero. La fuerza requerida depende del tiempo de frenado $ \Delta t $.

$$ F = \frac{\Delta p}{\Delta t} $$

Si el coche se detiene en $\Delta t = 5 \,\text{s}$, la fuerza media es de 4000 N aplicada durante 5 segundos:

$$ F = \frac{\Delta p}{\Delta t} = \frac{20{,}000}{5} = 4{,}000 \,\text{N} $$

Si, en cambio, se frena bruscamente en solo $ \Delta t = 0.1 \,\text{s}$, la fuerza necesaria se dispara:

$$ F = \frac{\Delta p}{\Delta t} = \frac{20{,}000}{0.1} = 2{,}000{,}000 \,\text{N} $$

De ahí que los choques violentos generen fuerzas enormes y produzcan graves daños, mientras que una frenada progresiva reparte la fuerza en un intervalo mayor y reduce drásticamente el impacto.

Ejemplo 2

Una bola de bolos tiene una masa de $m_b = 7 \,\text{kg}$ y rueda a una velocidad de $v_b = 2 \,\text{m/s}$.

Su cantidad de movimiento es de 14 kg·m/s:

$$ p_b = m_b \cdot v_b = 7 \cdot 2 = 14 \,\text{kg·m/s} $$

Aunque la velocidad sea baja, transporta suficiente cantidad de movimiento como para derribar los bolos con facilidad.

En contraste, una pelota de ping-pong de masa $m_p = 0.0027 \,\text{kg}$ puede alcanzar velocidades de $v_p = 20 \,\text{m/s}$.

Su cantidad de movimiento es de tan solo 0.054 kg·m/s:

$$ p_p = m_p \cdot v_p = 0.0027 \cdot 20 \approx 0.054 \,\text{kg·m/s} $$

En resumen, incluso a gran velocidad, la pelota apenas transmite cantidad de movimiento y su impacto es insignificante.

Este ejemplo ilustra por qué la cantidad de movimiento resulta esencial: en una colisión importa tanto la velocidad como la masa.

Masa constante y variable

En la mayoría de los problemas de mecánica clásica se supone que la masa de un cuerpo es constante. En ese caso, la expresión es:

$$ \vec{p} = m \vec{v} $$

Aquí la masa $m$ es fija e independiente del tiempo.

No obstante, existen situaciones en las que la masa varía con el tiempo.

Ejemplo. El caso paradigmático es un cohete que expulsa combustible: a medida que se eyecta el propulsor, la masa del cohete disminuye durante el vuelo.

En estas condiciones, la segunda ley de Newton se aplica en su forma más general:

$$ \vec{F} = \frac{d\vec{p}}{dt} = \frac{d}{dt}(m\vec{v}) $$

Aquí la masa depende explícitamente del tiempo.

$$ \vec{F} = m \frac{d\vec{v}}{dt} + \vec{v}\,\frac{dm}{dt} $$

La expresión muestra con claridad que una variación de masa afecta al movimiento del mismo modo que lo hace una aceleración.

Ejemplo. Un caso sencillo es un coche: al comenzar el viaje el depósito de combustible está lleno y al terminar casi vacío, lo que reduce ligeramente la masa total. En la práctica la diferencia es pequeña, pero el principio sigue siendo válido. En sistemas con pérdidas o ganancias de masa significativas (cohetes, chorros de fluido, arena que cae de un recipiente, etc.), la cantidad de movimiento debe analizarse siempre con esta formulación general.

A velocidades cercanas a la de la luz, además, deben considerarse los efectos relativistas: según la relatividad especial de Einstein, la inercia de un cuerpo aumenta con la velocidad.

Cantidad de movimiento relativista

Cuando la velocidad de un objeto se aproxima a la velocidad de la luz, la mecánica clásica deja de ser una descripción válida de su movimiento.

En la teoría especial de la relatividad de Einstein, la masa en reposo $m_0$ permanece constante, pero la definición de la cantidad de movimiento adopta una nueva forma relativista, conocida como momento relativista:

$$ \vec{p} = \gamma m_0 \vec{v} \qquad\text{donde}\qquad  \gamma = \frac{1}{\sqrt{1 - \frac{v^2}{c^2}}} $$

A velocidades cotidianas, $\gamma \approx 1$, por lo que la expresión relativista se reduce naturalmente a la fórmula clásica habitual.

Cuando la velocidad se acerca al valor de $c$, el factor de Lorentz $\gamma$ crece sin límite y la cantidad de movimiento aumenta en la misma medida. Esta relación explica por qué ningún cuerpo con masa en reposo finita puede ser acelerado hasta alcanzar la velocidad de la luz.

Nota. En los primeros enfoques de la relatividad, era común introducir el concepto de masa relativista, definida como $ m_{\text{rel}} = \gamma m_0 $, para explicar el incremento de la cantidad de movimiento a altas velocidades. La física moderna, sin embargo, mantiene constante la masa en reposo $m_0$ y atribuye el aumento de $\vec{p}$ exclusivamente al factor de Lorentz $\gamma$.

En la relación $ \vec{p} = \gamma m_0 \vec{v} $, el término $\gamma \vec{v}$ tiene la misma estructura matemática que la velocidad propia $\vec{\eta} = d\vec{x}/d\tau$, definida con respecto al tiempo propio $\tau$ del objeto.

No obstante, en este contexto representa la componente espacial del cuatro-vector velocidad $ U^\mu $:

$$ U^\mu = (\gamma c,\ \gamma \vec{v}) = (\gamma c,\ \gamma v_x, \gamma v_y, \gamma v_z ) $$

Su parte espacial coincide con el factor $\gamma \vec{v}$ de la expresión de $\vec{p}$, pero forma parte de una magnitud cuatridimensional invariante, que conserva el mismo valor para todos los observadores inerciales.

De este modo, la conservación del cuatro-vector cantidad de movimiento $P^\mu = m_0 U^\mu$ garantiza la conservación simultánea de la energía y de la cantidad de movimiento en cualquier sistema de referencia inercial.

El vínculo entre fuerza y cantidad de movimiento

La fuerza se define como la derivada temporal de la cantidad de movimiento: $$ \vec{F} = \frac{d \ \vec{p}}{dt} $$

Así, conocer la cantidad de movimiento de un cuerpo permite calcular la fuerza necesaria para frenarlo o detenerlo.

La fórmula $F = dp/dt$ no es más que una versión general de la segunda ley de Newton $F = ma$.

Derivación

Si consideramos masa constante:

$$ \vec{p} = m \cdot \vec{v} $$

Según la segunda ley de Newton, la fuerza equivale a la masa multiplicada por la aceleración:

$$ \vec{F} = m \cdot \vec{a} $$

Como la aceleración $a = dv/dt$, se obtiene:

$$ \vec{F} = m \cdot \frac{d\vec{v}}{dt} $$

Con $m$ constante, esto se reduce a:

$$ \vec{F} = \frac{d(m\vec{v})}{dt} = \frac{d\vec{p}}{dt} $$

Explicación. La derivada temporal de la cantidad de movimiento es $$ D[ \vec{p} ] = D[ m \cdot \vec{v} ] $$ Con $m$ constante, $$ D[ \vec{p} ] = m \cdot D[ \vec{v} ] $$

y así sucesivamente.