Momento de un par de fuerzas
El momento de un par de fuerzas describe la capacidad de un sistema de dos fuerzas para producir rotación. Se obtiene con la expresión $$ M = F \cdot d $$ donde $ F $ es la magnitud de una de las fuerzas y $ d $ es la distancia entre sus líneas de acción.
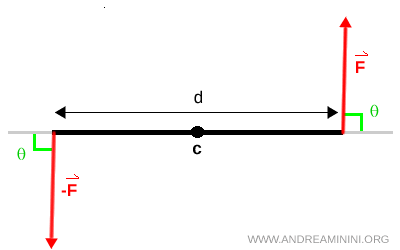
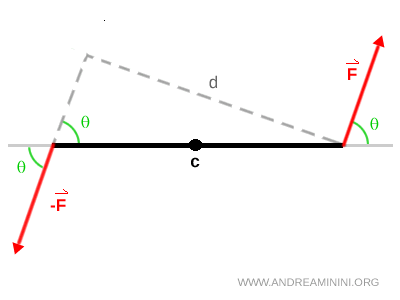
Cuando las fuerzas no son perpendiculares a la línea que une sus puntos de aplicación, la fórmula general es $$ M = F \cdot d \cdot \sin\theta $$ siendo $ \theta $ el ángulo entre la fuerza y la línea de unión.
Un par de fuerzas está formado por dos fuerzas paralelas, iguales en magnitud y opuestas en dirección. Este sistema no genera traslación; su único efecto es la rotación del cuerpo o mecanismo sobre el que actúa.
La separación entre las líneas de acción se conoce como brazo del par. Aunque las fuerzas se cancelan como resultante lineal, el sistema sigue produciendo un giro neto porque actúan sobre lados opuestos del cuerpo, generando rotación sin movimiento lineal.
Nota. El convenio de signos es el mismo que para el momento de una sola fuerza: el momento es positivo ( $ M > 0 $ ) si la rotación es antihoraria y negativo ( $ M < 0 $ ) si es horaria. Si $ M = 0 $ no se produce giro.
Ejemplo práctico
Imaginemos una válvula hidráulica accionada con ambas manos. La mano izquierda ejerce una fuerza hacia abajo y la derecha una fuerza hacia arriba, cada una de $ F = 8 \ N $.
Cada mano se coloca a $ 10 \ cm $ del centro y aplica la fuerza perpendicular al brazo, tal como muestra la ilustración.
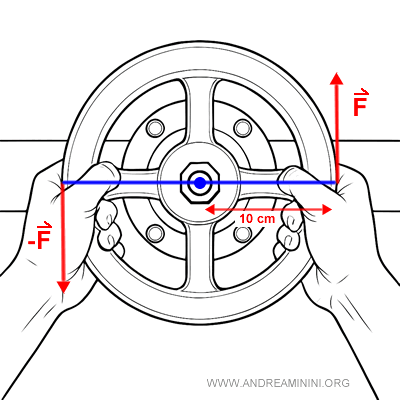
La acción conjunta de ambas fuerzas genera un par capaz de hacer girar la válvula:
$$ M = F \cdot d $$
La distancia entre las fuerzas es $ 10 \ cm + 10 \ cm = 20 \ cm $.
$$ M = F \cdot ( 20 \ cm ) $$
Convertimos a metros:
$$ M = F \cdot ( 0.2 \ m ) $$
Considerando solo una de las fuerzas:
$$ M = ( 8 \ N ) \cdot ( 0.2 \ m ) $$
$$ M = 1.6 \ Nm $$
El par generado tiene un momento de 1.6 Nm.
Segundo ejemplo
Mantenemos la misma situación, pero ahora las fuerzas se aplican formando un ángulo de 110° respecto al brazo.
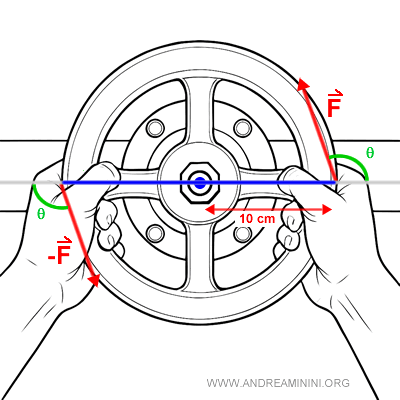
Los demás valores no cambian: cada mano ejerce $ 8 \ N $ a $ 10 \ cm $ del centro.
En este caso, el momento debe tener en cuenta el ángulo:
$$ M = F \cdot d \cdot \sin\theta $$
$$ M = ( 8 \ N ) \cdot ( 0.2 \ m ) \cdot \sin 110° $$
Usando la identidad $ \sin \theta = \sin (180° - \theta ) $, se obtiene:
$$ \sin 110° = \sin 70° $$
Por tanto:
$$ M = ( 8 \ N ) \cdot ( 0.2 \ m ) \cdot \sin 70° $$
$$ M = ( 8 \ N ) \cdot ( 0.2 \ m ) \cdot 0.94 $$
$$ M \approx 1.50 \ Nm $$
En este caso, el momento del par es ligeramente menor, ya que las fuerzas no actúan de manera perpendicular al brazo de la válvula. La misma metodología puede aplicarse a cualquier otra configuración geométrica.