Presión
La presión (p) es una magnitud física que describe cuán intensamente actúa una fuerza sobre una superficie. Se define como el cociente entre la componente de la fuerza perpendicular a la superficie, $ F_{\perp} $, y el área $ A $ sobre la que dicha fuerza se ejerce. $$ p = \frac{F_{\perp}}{A} $$
Para que exista presión, la fuerza debe actuar de forma perpendicular a la superficie. Si la fuerza está inclinada, solo su componente normal contribuye a la presión.
Cuando la fuerza es completamente perpendicular a la superficie, la definición se simplifica y queda:
$$ p = \frac{F}{A} $$
Esta expresión permite entender de inmediato una idea clave: la presión aumenta cuando aumenta la fuerza aplicada y disminuye cuando aumenta el área sobre la que se distribuye esa fuerza.
Por este motivo, es posible duplicar la presión de dos maneras distintas: duplicando la fuerza o reduciendo el área a la mitad. En ambos casos, el valor final de la presión es el mismo.
$$ 2p = \frac{2F}{A} = \frac{F}{\frac{A}{2}} $$
De ello se deduce que una misma fuerza aplicada sobre una superficie más pequeña produce una presión mayor.
Un ejemplo cotidiano lo aclara fácilmente. Al presionar un globo con el dedo, la presión es relativamente baja, ya que la fuerza se reparte sobre un área de contacto bastante grande. El globo se deforma, pero no se rompe. En cambio, si se aplica la misma fuerza con un alfiler, la presión aumenta de forma drástica, porque la fuerza se concentra en un área muy pequeña, y el globo estalla.

En otras palabras, cuando se aplica una fuerza sobre una superficie, su efecto no depende únicamente de la intensidad de esa fuerza, sino también del área sobre la que se reparte. Por este motivo, un globo no se rompe al presionarlo con un dedo, mientras que se rompe con facilidad cuando se lo toca con un alfiler.
La presión es una magnitud fundamental para comprender cómo se transmiten las fuerzas en los materiales sólidos y en los fluidos, y desempeña un papel central en numerosos fenómenos físicos y aplicaciones técnicas.
La unidad de medida de la presión
La presión es una magnitud escalar, ya que queda completamente determinada por un valor numérico que expresa su intensidad y por una unidad de medida.
En el Sistema Internacional de Unidades (SI), la unidad de presión es el pascal (Pa).
$$ 1 \ \text{Pa} = 1 \ \frac{\text{N}}{\text{m}^2} $$
Esto significa que una presión de 1 pascal corresponde al efecto de una fuerza de 1 newton distribuida uniformemente sobre una superficie de 1 metro cuadrado.
El nombre "pascal" se adoptó en honor al físico francés Blaise Pascal (1623-1662), cuyos estudios fueron fundamentales para el desarrollo de la mecánica de los fluidos y la comprensión de la presión.
Nota. Desde el punto de vista del análisis dimensional, la presión se define como el cociente entre una fuerza y un área, es decir, una longitud (L) elevada al cuadrado: \[ p = \frac{[F]}{[L^2]} \] La fuerza \( F \) tiene dimensiones \([M \cdot L \cdot T^{-2}] \), correspondientes a masa por aceleración, mientras que el área tiene dimensiones \([L^2] \). Al sustituir en la expresión se obtiene: \[ [p] = \frac{[M \cdot L \cdot T^{-2}]}{[L^2]} = [M \cdot L^{-1} \cdot T^{-2}] \] Esta es la dimensión física del pascal y refleja con claridad el significado físico de la presión.
La presión se mide mediante instrumentos denominados manómetros o medidores de presión. Existen distintos tipos, diseñados en función del fluido considerado y del intervalo de presiones que se desea medir, tanto en gases como en líquidos, y en situaciones de baja y de alta presión.
Ejemplo de cálculo
En este ejemplo se calcula la presión ejercida sobre la superficie de un globo cuando se aplica una fuerza de \( 2.6 \ \text{N} \), comparando dos situaciones muy distintas desde el punto de vista físico:
- a) el contacto con un dedo, cuyo área de contacto es \( 1.1 \cdot 10^{-4} \ \text{m}^2 \)
- b) el contacto con un alfiler, cuya punta tiene un área de \( 2.1 \cdot 10^{-7} \ \text{m}^2 \)
Además, sabiendo que el globo se rompe cuando la presión alcanza \( 4.1 \cdot 10^{5} \ \text{Pa} \), se determina la fuerza mínima necesaria para provocar la rotura en cada uno de los dos casos.
a] Presión ejercida por el dedo
Se aplica una fuerza \( F = 2.6 \ \text{N} \) sobre un área \( A = 1.1 \cdot 10^{-4} \ \text{m}^2 \), que corresponde al área de contacto del dedo.
La presión ejercida por el dedo se obtiene directamente a partir de la definición de presión:
\[ p = \frac{F}{A} = \frac{2.6 \ \text{N}}{1.1 \cdot 10^{-4} \ \text{m}^2} \]
Recordando que el pascal se define como $ Pa = \frac{\text{N}}{\text{m}^2} $, y realizando el cálculo, se obtiene:
\[ p \approx 2.36 \cdot 10^{4} \ \text{Pa} \]
Este valor es relativamente bajo, ya que la fuerza aplicada se distribuye sobre una superficie de contacto amplia.
b] Presión ejercida por el alfiler
En este segundo caso, la misma fuerza \( F = 2.6 \ \text{N} \) se aplica sobre un área mucho menor, \( A = 2.1 \cdot 10^{-7} \ \text{m}^2 \), correspondiente a la punta del alfiler.
La presión ejercida por el alfiler se calcula como:
\[ p = \frac{F}{A} = \frac{2.6 \ \text{N}}{2.1 \cdot 10^{-7} \ \text{m}^2} \]
Utilizando de nuevo la definición del pascal y efectuando el cálculo, se obtiene:
\[ p \approx 1.24 \cdot 10^{7} \ \text{Pa} \]
La presión es aquí varios órdenes de magnitud mayor, porque la misma fuerza se concentra en una región extremadamente pequeña.
c] Fuerza mínima necesaria para romper el globo con un alfiler
Si la presión de rotura del globo es \( p = 4.1 \cdot 10^{5} \ \text{Pa} \), la fuerza mínima necesaria se obtiene despejando la fuerza en la definición de presión:
\[ F = pA \]
Sustituyendo el valor de la presión de rotura y el área de la punta del alfiler \( A = 2.1 \cdot 10^{-7} \ \text{m}^2 \), resulta:
\[ F = (4.1 \cdot 10^{5} \ \text{Pa}) \cdot (2.1 \cdot 10^{-7} \ \text{m}^2) \]
Recordando que $ Pa = \frac{\text{N}}{\text{m}^2} $:
\[ F = (4.1 \cdot 10^{5} \ \frac{\text{N}}{\text{m}^2}) \cdot (2.1 \cdot 10^{-7} \ \text{m}^2) \]
\[ F = (4.1 \cdot 10^{5} \ \text{N}) \cdot (2.1 \cdot 10^{-7} ) \]
\[ F = 8.61 \cdot 10^{-2} \ \text{N} \]
Por lo tanto, la fuerza mínima requerida es:
\( F_{\min} \approx 0.086 \ \text{N} \)
Este valor explica por qué un alfiler permite romper el globo con un esfuerzo muy pequeño.
d] Fuerza mínima necesaria para romper el globo con un dedo
El procedimiento es el mismo. A partir de la definición de presión \( p = \frac{F}{A} \), la fuerza se expresa como:
\[ F = pA \]
La presión de rotura es \( p = 4.1 \cdot 10^{5} \ \text{Pa} \) y el área de contacto del dedo es \( A = 1.1 \cdot 10^{-4} \ \text{m}^2 \).
\[ F = (4.1 \cdot 10^{5} \ \text{Pa}) \cdot (1.1 \cdot 10^{-4} \ \text{m}^2) \]
Recordando que $ Pa = \frac{\text{N}}{\text{m}^2} $:
\[ F = (4.1 \cdot 10^{5} \ \frac{\text{N}}{\text{m}^2}) \cdot (1.1 \cdot 10^{-4} \ \text{m}^2) \]
\[ F = (4.1 \cdot 10^{5} \ \text{N}) \cdot (1.1 \cdot 10^{-4} ) \]
Al combinar las potencias de diez \( 10^{5} \cdot 10^{-4} = 10^{1} \) y multiplicar los coeficientes numéricos \( 4.1 \cdot 1.1 = 4.51 \), se obtiene:
\[ F = 4.51 \cdot 10^{1} \ \text{N} \]
Por lo tanto, la fuerza mínima requerida es:
\[ F_{\min} \approx 45 \ \text{N} \]
Este resultado pone de manifiesto que, para un mismo valor de presión crítica, la fuerza necesaria depende de manera decisiva del área sobre la que se aplica. Cuanto menor es el área de contacto, mayor es la presión generada a igualdad de fuerza.
Presión en los fluidos
La presión en un fluido es la fuerza que el fluido ejerce por unidad de superficie sobre las paredes del recipiente que lo contiene, sobre los cuerpos sumergidos y sobre las regiones vecinas del propio fluido.
Esta presión actúa siempre de forma normal, es decir, perpendicular a la superficie sobre la que se aplica, ya sea la pared de un recipiente, la superficie de un objeto inmerso o una superficie ideal imaginada dentro del fluido.
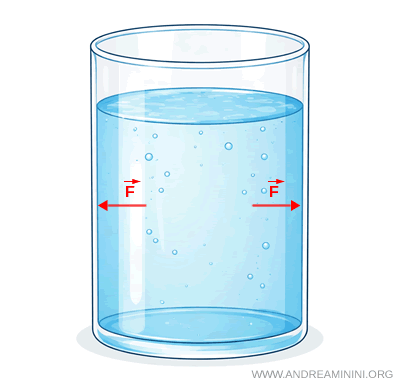
Cuando un fluido está en equilibrio, es decir, cuando permanece en reposo, la presión presenta una propiedad clave: en cualquier punto del fluido tiene el mismo valor en todas las direcciones.
Para entender mejor esta propiedad, pensemos en un punto cualquiera dentro de un fluido en equilibrio y en una superficie imaginaria que pasa por ese punto. Sobre cada una de las caras de la superficie actúan fuerzas de presión perpendiculares a ella. Estas fuerzas tienen la misma magnitud y sentidos opuestos, por lo que se compensan exactamente.

Si cambiamos la orientación de la superficie imaginaria, la dirección de la fuerza ejercida por el fluido cambia en consecuencia, pero el valor de la presión no se altera. Esto muestra que la presión no depende de la orientación de la superficie y es la misma en todas las direcciones.
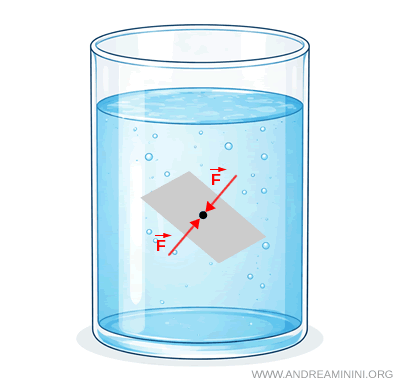
Nota. Como la presión no está asociada a ninguna dirección preferente, no es una magnitud vectorial. La presión es una magnitud escalar.
En otras palabras, en cada punto de un fluido en equilibrio actúan fuerzas de presión iguales y opuestas en todas las direcciones.
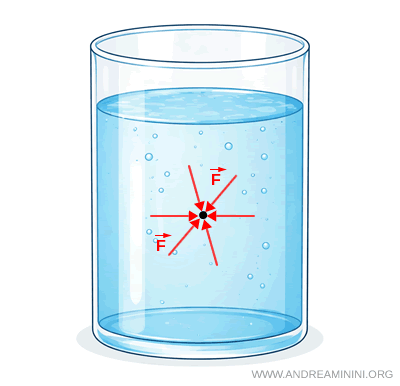
Si esta condición no se cumpliera, las fuerzas dejarían de compensarse, aparecería una fuerza resultante y el fluido empezaría a moverse.
Por ello, la isotropía de la presión es una condición imprescindible para que un fluido pueda mantenerse en equilibrio mecánico.
Diferencia entre la presión en sólidos y en líquidos
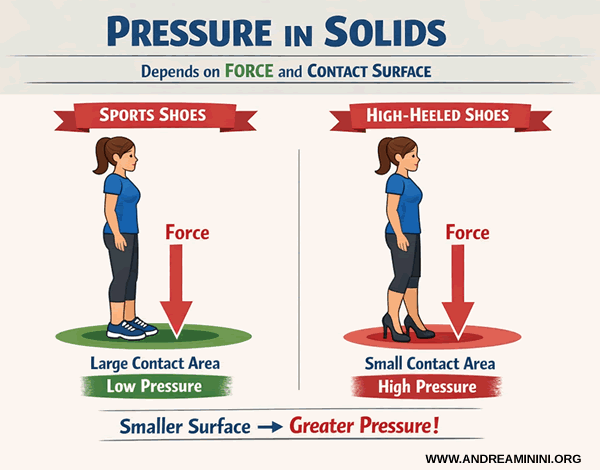
La presión no se manifiesta del mismo modo en sólidos y en líquidos. En los sólidos, depende de dos factores: la magnitud de la fuerza aplicada y el área de contacto sobre la que esa fuerza se distribuye.
Un ejemplo cotidiano lo ilustra con claridad. Una persona con zapatillas ejerce menos presión sobre el suelo que la misma persona con zapatos de tacón. La fuerza es la misma, pero el área de apoyo es mucho menor.
En los líquidos, la situación es diferente. La presión está determinada principalmente por la profundidad. Cuanto más profundo se encuentra un punto dentro del fluido, mayor es la presión ejercida por el líquido.
La razón es física. A mayor profundidad, mayor es el peso de la columna de fluido situada por encima. Por ello, en un fluido en reposo, la presión aumenta con la profundidad y se transmite uniformemente en todas las direcciones.

Presión atmosférica
La atmósfera también ejerce presión. La presión atmosférica es la presión que el aire ejerce sobre todas las superficies debido al peso de la columna de aire suprayacente.
El aire tiene masa y, en consecuencia, peso. A nivel del mar, la presión atmosférica estándar vale aproximadamente:
\[ p_{at} = 1.013 \cdot 10^5 \ \text{Pa} \]
Aunque no la percibamos de forma directa, esta presión actúa constantemente sobre todos los cuerpos y sobre cada parte del cuerpo humano.

Ejemplos adicionales
Ejemplo 1
Una pelota con una presión interna manométrica (relativa) de \( p = 8.0 \times 10^4 \ Pa \) se presiona contra el suelo mediante una fuerza \( F = 40 \ N \) y posteriormente rebota. ¿Cuál es el área de contacto entre la pelota y el suelo?
Partimos de la definición de presión
$$ p = \dfrac{F}{A} $$
Despejamos el área
$$ A = \dfrac{F}{p} $$
Sustituimos los valores \( F = 40 \ N \) y \( p = 8.0 \times 10^4 \ Pa \)
$$ A = \dfrac{40}{8.0 \times 10^4} = 5.0 \times 10^{-4} \ m^2 $$
Convertimos a centímetros cuadrados
$$ 5.0 \times 10^{-4} \ m^2 = 5.0 \ cm^2 $$
Por lo tanto, el área de contacto es 5 cm2.
¿Cuál es el diámetro del área de contacto?
Suponemos que la zona de contacto es circular. Utilizamos la fórmula del área del círculo
$$ A = \pi \left(\dfrac{d}{2}\right)^2 $$
Despejamos el diámetro
$$ d = 2 \sqrt{\dfrac{A}{\pi}} $$
Sustituimos el área calculada
$$ d = 2 \sqrt{\dfrac{5.0 \times 10^{-4}}{\pi}} $$
Evaluamos la expresión
$$ \dfrac{5.0 \times 10^{-4}}{\pi} \approx 1.59 \times 10^{-4} $$
$$ \sqrt{1.59 \times 10^{-4}} \approx 0.0126 \ m $$
$$ d \approx 2 \times 0.0126 = 0.0252 \ m $$
Convertimos a centímetros
$$ d = 2.52 \ cm \approx 2.5 \ cm $$
Así, el diámetro de contacto es aproximadamente \( d \approx 2.5 \ cm \).
¿Cuál es la presión interna absoluta de la pelota?
La presión absoluta se calcula sumando la presión manométrica y la presión atmosférica
$$ p_{abs} = p_{man} + p_{at} $$
La presión dada \( p = 8.0 \times 10^4 \ Pa \) corresponde a \( p_{man} \).
Usamos \( p_{at} \approx 1.0 \times 10^5 \ Pa \)
$$ p_{abs} = 8.0 \times 10^4 + 1.0 \times 10^5 $$
$$ p_{abs} = 1.8 \times 10^5 \ Pa $$
Dado que \( 1 \ \text{atm} \approx 1.013 \times 10^5 \ Pa \), la presión interna absoluta es aproximadamente 1.8 atm.
Y así sucesivamente.