Centro de masas
El centro de masas es el punto donde puede considerarse concentrada toda la masa de un objeto o de un sistema. Este punto nos permite analizar su movimiento y las fuerzas que actúan sobre él de una manera más clara y manejable.
Aunque es un concepto abstracto, resulta fundamental en mecánica. Gracias al centro de masas, un objeto extenso y con forma compleja puede estudiarse como si fuera un único punto. Esto simplifica el análisis sin perder la esencia física del problema.
El centro de masas se comporta como si todas las fuerzas externas actuaran directamente sobre él. Por eso su movimiento describe la traslación global del sistema y se convierte en una herramienta central en cualquier estudio dinámico.
En el caso de un cuerpo rígido, solemos modelar su traslación como la de una sola partícula situada en el centro de masas. Esta idealización reduce considerablemente la complejidad de los cálculos.
¿Cómo se localiza el centro de masas?
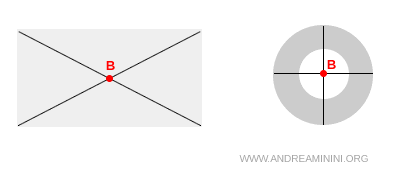
Su posición depende de cómo esté repartida la masa en el objeto. En cuerpos uniformes o simétricos coincide con el centroide, que es el punto geométrico de equilibrio.
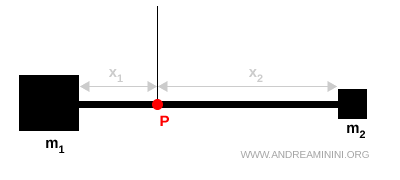
Veamos un ejemplo sencillo. Una barra rígida con dos masas, $m_1$ y $m_2$, situadas en sus extremos y suspendida de un punto P. La barra se mantiene horizontal cuando los momentos de fuerza alrededor de P se equilibran.
$$ m_1 x_1 = m_2 x_2 $$
Si esta igualdad se cumple, P coincide con el centro de masas del sistema.
Nota. En este ejemplo se omite la masa de la propia barra para simplificar. Si fuese relevante, habría que incluir su peso en el equilibrio de momentos.
En objetos de forma irregular, el centro de masas puede determinarse de forma experimental. Basta con colgarlos de dos puntos distintos y trazar las verticales que pasan por cada punto de suspensión.
Por ejemplo, si colgamos una raqueta de tenis desde \( P_1 \) y la dejamos alcanzar el equilibrio, sabemos que el centro de masas está en algún punto de la vertical \( r_1 \).
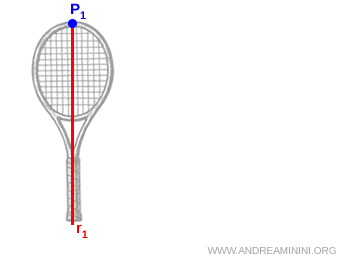
Nota. En equilibrio, el momento neto sobre la raqueta es cero. Por ello permanece inmóvil una vez que se estabiliza.
Si repetimos el procedimiento desde un segundo punto \( P_2 \), obtenemos otra vertical \( r_2 \).
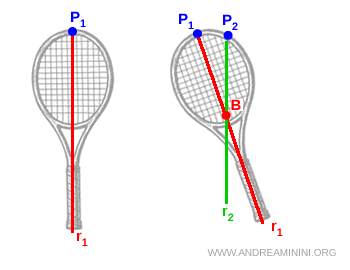
Las dos rectas se cruzan en un único punto \( B \), que es el centro de masas de la raqueta.
Un ejemplo práctico
Imaginemos ahora una caja de 10 kg colocada sobre un plano inclinado.
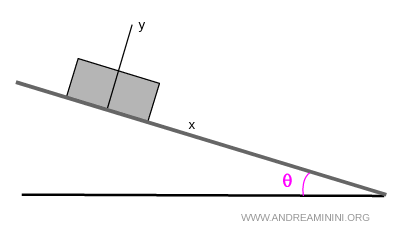
Sobre ella actúan tres fuerzas principales: el peso, la fuerza normal del plano y la fricción. Para estudiar el equilibrio y el movimiento, es suficiente con considerar que todas actúan en un único punto, el centroide \( C \).
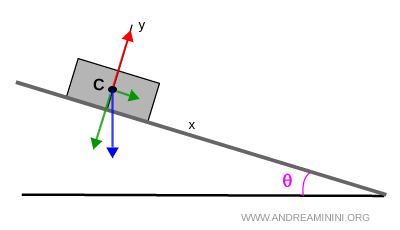
Este enfoque permite descomponer las fuerzas de manera sencilla y entender cómo se combinan para producir el movimiento.
Nota. La simplificación es válida cuando la masa está distribuida uniformemente. Si no fuese así, habría que calcular el centro de masas real según la distribución de masas del objeto.
Ejemplo 2
Supongamos ahora una masa de 2 kg situada en 0 m y otra de 3 kg situada en 4 m sobre una barra horizontal.

Tenemos entonces $m_1 = 2 \ kg$ y $m_2 = 3 \ kg$ en las posiciones $x_1 = 0 \ m$ y $x_2 = 4 \ m$ respectivamente.
El centro de masas se calcula con la fórmula habitual:
$$ x_{cm} = \frac{ m_1 x_1 + m_2 x_2 }{ m_1 + m_2 } $$
$$ x_{cm} = \frac{2 \cdot 0 + 3 \cdot 4}{2 + 3} = \frac{12}{5} = 2.4 \, \text{m}
$$
El resultado confirma que el centro de masas se sitúa más cerca de la masa mayor, lo cual coincide con la intuición física.
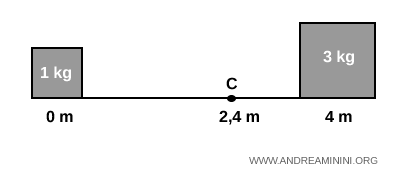
Una vez encontrado el centro de masas, el movimiento del sistema puede analizarse como si se tratara de una sola partícula. Esta idea será útil en muchos otros problemas de dinámica.